Boltzmann machine
Encyclopedia
A Boltzmann machine is a type of stochastic recurrent neural network
invented by Geoffrey Hinton
and Terry Sejnowski
. Boltzmann machines can be seen as the stochastic
, generative
counterpart of Hopfield net
s. They were one of the first examples of a neural network capable of learning internal representations, and are able to represent and (given sufficient time) solve difficult combinatoric problems. However, due to a number of issues discussed below, Boltzmann machines with unconstrained connectivity have not proven useful for practical problems in machine learning or inference. They are still theoretically intriguing, however, due to the locality and Hebbian nature of their training algorithm, as well as their parallelism and the resemblance of their dynamics to simple physical processes. If the connectivity is constrained, the learning can be made efficient enough to be useful for practical problems.
They are named after the Boltzmann distribution
in statistical mechanics, which is used in their sampling function.
work, is a network of units with an "energy" defined for the network. It also has binary units, but unlike Hopfield nets, Boltzmann machine units are stochastic
. The global energy,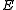
, in a Boltzmann machine is identical in form to that of a Hopfield network:
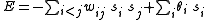
Where:
The connections in a Boltzmann machine have two restrictions:
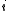being 0 (off) versus 1 (on), written 
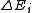, is given by:
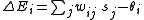
This can be expressed as the difference of energies of two states:
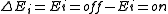
We then substitute the energy of each state with its relative probability according to the Boltzmann Factor
(the property of a Boltzmann distribution
that the energy of a state is proportional to the negative log probability of that state):
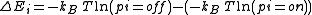
where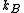
is Boltzmann's constant and becomes lumped into the artificial notion of temperature 
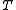. We then rearrange terms and consider that the probabilities of the unit being on and off must sum to one:
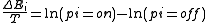
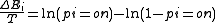
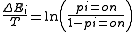
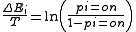
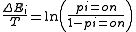
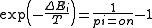
We can now finally solve for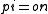
, the probability that the 
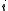-th unit is on.
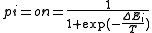
where the scalar
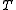is referred to as the temperature
of the system. This relation is the source of the logistic function
found in probability expressions in variants of the Boltzmann machine.
. This means that log-probabilities of global states become linear in their energies. This relationship is true when the machine is "at thermal equilibrium
", meaning that the probability distribution of global states has converged. If we start running the network from a high temperature, and gradually decrease it until we reach a thermal equilibrium
at a low temperature, we are guaranteed to converge to a distribution where the energy level fluctuates around the global minimum. This process is called simulated annealing
.
If we want to train the network so that the chance it will converge to a global state is according to an external distribution that we have over these states, we need to set the weights so that the global states with the highest probabilities will get the lowest energies. This is done by the following training procedure.
.
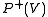As is discussed above, the distribution over global states converges as the Boltzmann machine reaches thermal equilibrium
. We denote this distribution, after we marginalize it over the hidden units, as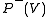
.
Our goal is to approximate the "real" distribution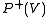
using the 
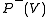which will be produced (eventually) by the machine. To measure how similar the two distributions are, we use the Kullback-Leibler divergence, 
:
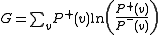
Where the sum is over all the possible states of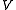
. 
is a function of the weights, since they determine the energy of a state, and the energy determines 
, as promised by the Boltzmann distribution
. Hence, we can use a gradient descent
algorithm over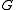
, so a given weight, 
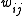is changed by subtracting the partial derivative
of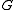
with respect to the weight.
There are two phases to Boltzmann machine training, and we switch iteratively between them. One is the "positive" phase where the visible units' states are clamped to a particular binary state vector sampled from the training set (according to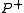
). The other is the "negative" phase where the network is allowed to run freely, i.e. no units have their state determined by external data. Surprisingly enough, the gradient with respect to a given weight, 
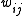, is given by the very simple equation (proved in Ackley et al.):
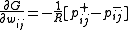
Where:
This result follows from the fact that at thermal equilibrium
the probability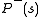
of any global state 
when the network is free-running is given by the Boltzmann distribution
(hence the name "Boltzmann machine").
Remarkably, this learning rule is fairly biologically plausible because the only information needed to change the weights is provided by "local" information. That is, the connection (or synapse
biologically speaking) does not need information about anything other than the two neurons it connects. This is far more biologically realistic than the information needed by a connection in many other neural network training algorithms, such as backpropagation
.
The training of a Boltzmann machine does not use the EM algorithm, which is heavily used in machine learning
.
By minimizing the KL-divergence, it is equivalent as maximizing the log-likelihood of the data. Therefore, the training procedure performs gradient ascent on the log-likelihood of the observed data. This is in contrast to the EM algorithm, where the posterior distribution of the hidden nodes must be calculated before the maximization of the expected value of the complete data likelihood during the M-step.
Training the biases is similar, but uses only single node activity:
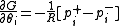
Unfortunately, there is a serious practical problem with the Boltzmann machine, namely that the learning seems to stop working correctly when the machine is scaled up to anything larger than a trivial machine. This is due to a number of effects, the most important of which are:
an architecture called the "restricted Boltzmann machine" or "RBM" which does not allow intralayer connections between hidden units. After training one RBM, the activities of its hidden units can be treated as data for training a higher-level RBM. This method of stacking RBM's makes it possible to train many layers of hidden units efficiently and is one of the most common deep learning
strategies. As each new layer is added the overall generative model gets better.
There is an extension to the restricted Boltzmann machine that affords using real valued data rather than binary data. Along with higher order Boltzmann machines, it is outlined here http://www.youtube.com/watch?v=VdIURAu1-aU.
version of the Hopfield net
work.
The idea of using annealed Ising model
s for inference is often thought to have been first described by:
However, it should be noted that these articles appeared after the seminal publication by John Hopfield, where the connection to physics and statistical mechanics was made in the first place, mentioning spin glasses:
The idea of applying the Ising model with annealed Gibbs sampling
is also present in Douglas Hofstadter
's Copycat
project:
Similar ideas (with a change of sign in the energy function) are also found in Paul Smolensky
's "Harmony Theory".
The explicit analogy drawn with statistical mechanics in the Boltzmann Machine formulation led to the use of terminology borrowed from physics (e.g., "energy" rather than "harmony"), which has become standard in the field. The widespread adoption of this terminology may have been encouraged by the fact that its use led to the importation of a variety of concepts and methods from statistical mechanics.
However, there is no reason to think that the various proposals to use simulated annealing for inference described above were not independent.
(Helmholtz
made a similar analogy during the dawn of psychophysics.)
Ising models are now considered to be a special case of Markov random fields, which find widespread application in various fields, including linguistics
, robotics
, computer vision
, and artificial intelligence
.
Stochastic neural network
Stochastic neural networks are a type of artificial neural networks, which is a tool of artificial intelligence. They are built by introducing random variations into the network, either by giving the network's neurons stochastic transfer functions, or by giving them stochastic weights...
invented by Geoffrey Hinton
Geoffrey Hinton
Geoffrey Hinton is a British born informatician most noted for his work on the mathematics and applications of neural networks, and their relationship to information theory.-Career:...
and Terry Sejnowski
Terry Sejnowski
Terrence Joseph Sejnowski is an Investigator with the Howard Hughes Medical Institute and is the Francis Crick Professor at The Salk Institute for Biological Studies where he directs the Computational Neurobiology Laboratory...
. Boltzmann machines can be seen as the stochastic
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
, generative
Generative model
In probability and statistics, a generative model is a model for randomly generating observable data, typically given some hidden parameters. It specifies a joint probability distribution over observation and label sequences...
counterpart of Hopfield net
Hopfield net
A Hopfield network is a form of recurrent artificial neural network invented by John Hopfield. Hopfield nets serve as content-addressable memory systems with binary threshold units. They are guaranteed to converge to a local minimum, but convergence to one of the stored patterns is not guaranteed...
s. They were one of the first examples of a neural network capable of learning internal representations, and are able to represent and (given sufficient time) solve difficult combinatoric problems. However, due to a number of issues discussed below, Boltzmann machines with unconstrained connectivity have not proven useful for practical problems in machine learning or inference. They are still theoretically intriguing, however, due to the locality and Hebbian nature of their training algorithm, as well as their parallelism and the resemblance of their dynamics to simple physical processes. If the connectivity is constrained, the learning can be made efficient enough to be useful for practical problems.
They are named after the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
in statistical mechanics, which is used in their sampling function.
Structure
A Boltzmann machine, like a Hopfield netHopfield net
A Hopfield network is a form of recurrent artificial neural network invented by John Hopfield. Hopfield nets serve as content-addressable memory systems with binary threshold units. They are guaranteed to converge to a local minimum, but convergence to one of the stored patterns is not guaranteed...
work, is a network of units with an "energy" defined for the network. It also has binary units, but unlike Hopfield nets, Boltzmann machine units are stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
. The global energy,
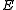, in a Boltzmann machine is identical in form to that of a Hopfield network: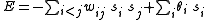Where:
-
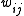is the connection strength between unit 
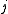and unit 
. -
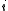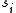is the state, 
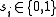, of unit 
. -
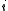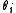is the threshold of unit 
.
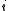The connections in a Boltzmann machine have two restrictions:
-
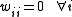. (No unit has a connection with itself.) -
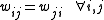. (All connections are symmetric.)
Probability of a unit's state
The difference in the global energy that results from a single unit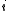 being 0 (off) versus 1 (on), written 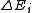, is given by: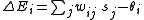This can be expressed as the difference of energies of two states:
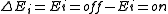
We then substitute the energy of each state with its relative probability according to the Boltzmann Factor
Boltzmann factor
In physics, the Boltzmann factor is a weighting factor that determines the relative probability of a particle to be in a state i in a multi-state system in thermodynamic equilibrium at temperature T...
(the property of a Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
that the energy of a state is proportional to the negative log probability of that state):
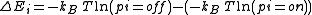
where
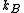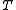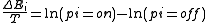
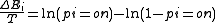
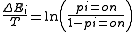
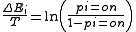
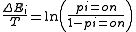
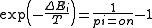
is Boltzmann's constant and becomes lumped into the artificial notion of temperature . We then rearrange terms and consider that the probabilities of the unit being on and off must sum to one:We can now finally solve for
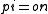, the probability that the 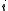-th unit is on.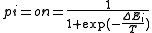where the scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
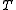is referred to as the temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
of the system. This relation is the source of the logistic function
Logistic function
A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
found in probability expressions in variants of the Boltzmann machine.
Equilibrium state
The network is run by repeatedly choosing a unit and setting its state according to the above formula. After running for long enough at a certain temperature, the probability of a global state of the network will depend only upon that global state's energy, according to a Boltzmann distributionBoltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
. This means that log-probabilities of global states become linear in their energies. This relationship is true when the machine is "at thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
", meaning that the probability distribution of global states has converged. If we start running the network from a high temperature, and gradually decrease it until we reach a thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
at a low temperature, we are guaranteed to converge to a distribution where the energy level fluctuates around the global minimum. This process is called simulated annealing
Simulated annealing
Simulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
.
If we want to train the network so that the chance it will converge to a global state is according to an external distribution that we have over these states, we need to set the weights so that the global states with the highest probabilities will get the lowest energies. This is done by the following training procedure.
Training
The units in the Boltzmann Machine are divided into "visible" units, V, and "hidden" units, H. The visible units are those which receive information from the "environment", i.e. our training set is a set of binary vectors over the set V. The distribution over the training set is denoted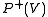.As is discussed above, the distribution over global states converges as the Boltzmann machine reaches thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
. We denote this distribution, after we marginalize it over the hidden units, as
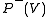.Our goal is to approximate the "real" distribution
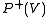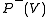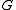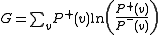
using the which will be produced (eventually) by the machine. To measure how similar the two distributions are, we use the Kullback-Leibler divergence, :Where the sum is over all the possible states of
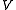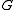. is a function of the weights, since they determine the energy of a state, and the energy determines 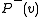, as promised by the Boltzmann distributionBoltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
. Hence, we can use a gradient descent
Gradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
algorithm over
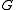, so a given weight, 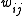is changed by subtracting the partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
of
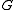with respect to the weight.There are two phases to Boltzmann machine training, and we switch iteratively between them. One is the "positive" phase where the visible units' states are clamped to a particular binary state vector sampled from the training set (according to
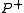). The other is the "negative" phase where the network is allowed to run freely, i.e. no units have their state determined by external data. Surprisingly enough, the gradient with respect to a given weight, 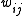, is given by the very simple equation (proved in Ackley et al.):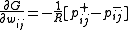Where:
-
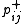is the probability of units i and j both being on when the machine is at equilibrium on the positive phase.
-
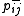is the probability of units i and j both being on when the machine is at equilibrium on the negative phase.
-
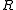denotes the learning rate
This result follows from the fact that at thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
the probability
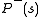of any global state when the network is free-running is given by the Boltzmann distributionBoltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
(hence the name "Boltzmann machine").
Remarkably, this learning rule is fairly biologically plausible because the only information needed to change the weights is provided by "local" information. That is, the connection (or synapse
Synapse
In the nervous system, a synapse is a structure that permits a neuron to pass an electrical or chemical signal to another cell...
biologically speaking) does not need information about anything other than the two neurons it connects. This is far more biologically realistic than the information needed by a connection in many other neural network training algorithms, such as backpropagation
Backpropagation
Backpropagation is a common method of teaching artificial neural networks how to perform a given task. Arthur E. Bryson and Yu-Chi Ho described it as a multi-stage dynamic system optimization method in 1969 . It wasn't until 1974 and later, when applied in the context of neural networks and...
.
The training of a Boltzmann machine does not use the EM algorithm, which is heavily used in machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
.
By minimizing the KL-divergence, it is equivalent as maximizing the log-likelihood of the data. Therefore, the training procedure performs gradient ascent on the log-likelihood of the observed data. This is in contrast to the EM algorithm, where the posterior distribution of the hidden nodes must be calculated before the maximization of the expected value of the complete data likelihood during the M-step.
Training the biases is similar, but uses only single node activity:
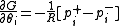
Problems
The Boltzmann machine would theoretically be a rather general computational medium. For instance, if trained on photographs, the machine would theoretically model the distribution of photographs, and could use that model to, for example, complete a partial photograph.Unfortunately, there is a serious practical problem with the Boltzmann machine, namely that the learning seems to stop working correctly when the machine is scaled up to anything larger than a trivial machine. This is due to a number of effects, the most important of which are:
- the time the machine must be run in order to collect equilibrium statistics grows exponentially with the machine's size, and with the magnitude of the connection strengths
- connection strengths are more plastic when the units being connected have activation probabilities intermediate between zero and one, leading to a so-called variance trap. The net effect is that noise causes the connection strengths to random walk until the activities saturate.
Restricted Boltzmann machine
Although learning is impractical in general Boltzmann machines, it can be made quite efficient inan architecture called the "restricted Boltzmann machine" or "RBM" which does not allow intralayer connections between hidden units. After training one RBM, the activities of its hidden units can be treated as data for training a higher-level RBM. This method of stacking RBM's makes it possible to train many layers of hidden units efficiently and is one of the most common deep learning
Deep learning
Deep learning is a sub-field within machine learning that uses deep architectures to model complex relationships among data. Such models have proven to be effective feature extractors over high-dimensional, structured data ....
strategies. As each new layer is added the overall generative model gets better.
There is an extension to the restricted Boltzmann machine that affords using real valued data rather than binary data. Along with higher order Boltzmann machines, it is outlined here http://www.youtube.com/watch?v=VdIURAu1-aU.
History
The Boltzmann machine is a Monte CarloMonte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
version of the Hopfield net
Hopfield net
A Hopfield network is a form of recurrent artificial neural network invented by John Hopfield. Hopfield nets serve as content-addressable memory systems with binary threshold units. They are guaranteed to converge to a local minimum, but convergence to one of the stored patterns is not guaranteed...
work.
The idea of using annealed Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
s for inference is often thought to have been first described by:
- Geoffrey E. Hinton and Terrence J. Sejnowski, Analyzing Cooperative Computation. In Proceedings of the 5th Annual Congress of the Cognitive Science Society, Rochester, NY, May 1983.
- Geoffrey E. Hinton and Terrence J. Sejnowski, Optimal Perceptual Inference. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition (CVPR), pages 448–453, IEEE Computer Society, Washington DC, June 1983.
However, it should be noted that these articles appeared after the seminal publication by John Hopfield, where the connection to physics and statistical mechanics was made in the first place, mentioning spin glasses:
- Jophn J. Hopfield, Neural networks and physical systems with emergent collective computational abilities, Proc. Natl. Acad. Sci. USA, vol. 79 no. 8, pp. 2554-2558, April 1982.
The idea of applying the Ising model with annealed Gibbs sampling
Gibbs sampling
In statistics and in statistical physics, Gibbs sampling or a Gibbs sampler is an algorithm to generate a sequence of samples from the joint probability distribution of two or more random variables...
is also present in Douglas Hofstadter
Douglas Hofstadter
Douglas Richard Hofstadter is an American academic whose research focuses on consciousness, analogy-making, artistic creation, literary translation, and discovery in mathematics and physics...
's Copycat
Copycat (software)
Copycat is a model of analogy making and human cognition based on the concept of the parallel terraced scan, developed in 1988 by Douglas Hofstadter, Melanie Mitchell, and others at the at , Indiana University Bloomington...
project:
- Hofstadter, Douglas R., The Copycat Project: An Experiment in Nondeterminism and Creative Analogies. MIT Artificial Intelligence Laboratory Memo No. 755, January 1984.
- Hofstadter, Douglas R., A Non-Deterministic Approach to Analogy, Involving the Ising Model of Ferromagnetism. In E. Caianiello, ed. The Physics of Cognitive Processes. Teaneck, NJ: World Scientific, 1987.
Similar ideas (with a change of sign in the energy function) are also found in Paul Smolensky
Paul Smolensky
Paul Smolensky is a professor of Cognitive Science at the Johns Hopkins University.Along with Alan Prince he developed Optimality Theory, a representational model of linguistics...
's "Harmony Theory".
The explicit analogy drawn with statistical mechanics in the Boltzmann Machine formulation led to the use of terminology borrowed from physics (e.g., "energy" rather than "harmony"), which has become standard in the field. The widespread adoption of this terminology may have been encouraged by the fact that its use led to the importation of a variety of concepts and methods from statistical mechanics.
However, there is no reason to think that the various proposals to use simulated annealing for inference described above were not independent.
(Helmholtz
Hermann von Helmholtz
Hermann Ludwig Ferdinand von Helmholtz was a German physician and physicist who made significant contributions to several widely varied areas of modern science...
made a similar analogy during the dawn of psychophysics.)
Ising models are now considered to be a special case of Markov random fields, which find widespread application in various fields, including linguistics
Linguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
, robotics
Robotics
Robotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
, computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, and artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
.