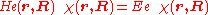Born-Oppenheimer approximation
Encyclopedia
In quantum chemistry
, the computation of the energy and wavefunction
of an average-size molecule
is a formidable task that is alleviated by the Born–Oppenheimer (BO) approximation, named after Max Born
and J. Robert Oppenheimer. For instance the benzene
molecule consists of 12 nuclei and 42 electrons. The time independent Schrödinger equation
, which must be solved to obtain the energy and molecular wavefunction of this molecule, is a partial differential eigenvalue equation
in 162 variables—the spatial coordinates of the electrons and the nuclei. The BO approximation makes it possible to compute the wavefunction in two less complicated consecutive steps. This approximation was proposed in 1927, in the early period of quantum mechanics, by Born and Oppenheimer and is still indispensable in quantum chemistry.
In basic terms, it allows the wavefunction of a molecule to be broken into its electronic and nuclear (vibrational, rotational) components.
In the first step of the BO approximation the electronic Schrödinger equation is solved, yielding the wavefunction depending on electrons only. For benzene this wavefunction depends on 126 electronic coordinates. During this solution the nuclei are fixed in a certain configuration, very often the equilibrium configuration. If the effects of the quantum mechanical nuclear motion are to be studied, for instance because a vibrational spectrum
depending on electrons only. For benzene this wavefunction depends on 126 electronic coordinates. During this solution the nuclei are fixed in a certain configuration, very often the equilibrium configuration. If the effects of the quantum mechanical nuclear motion are to be studied, for instance because a vibrational spectrum
is required, this electronic computation must be in nuclear coordinates. In the second step of the BO approximation this function serves as a potential in a Schrödinger equation containing only the nuclei—for benzene an equation in 36 variables.
The success of the BO approximation is due to the high ratio between nuclear and electronic masses. The approximation is an important tool of quantum chemistry; without it only the lightest molecule, H2, could be handled, and all computations of molecular wavefunctions for larger molecules make use of it. Even in the cases where the BO approximation breaks down, it is used as a point of departure for the computations.
The electronic energies, constituting the nuclear potential, consist of kinetic energies, interelectronic repulsions and electron–nuclear attractions. In a handwaving
manner the nuclear potential is taken to be an averaged electron–nuclear attraction.
The BO approximation follows from the inertia of electrons being considered to be negligible in comparison to the atom to which they are bound.
–Oppenheimer
(BO) approximation
is ubiquitous in quantum chemical
calculations of molecular wavefunction
s. It consists of two steps.
In the first step the nuclear kinetic energy
is neglected, that is, the corresponding operator Tn is subtracted from the total molecular Hamiltonian
. In the remaining electronic Hamiltonian He the nuclear positions enter as parameters. The electron–nucleus interactions are not removed and the electrons still "feel" the Coulomb potential of the nuclei clamped at certain positions in space. (This first step of the BO approximation is therefore often referred to as the clamped nuclei approximation.)
The electronic Schrödinger equation
is solved (out of necessity, approximately). The quantity r stands for all electronic coordinates and R for all nuclear coordinates. The electronic energy eigenvalue Ee depends on the chosen positions R of the nuclei. Varying these positions R in small steps and repeatedly solving the electronic Schrödinger equation
, one obtains Ee as a function of R. This is the potential energy surface
(PES): Ee(R) . Because this procedure of recomputing the electronic wave functions as a function of an infinitesimally changing nuclear geometry is reminiscent of the conditions for the adiabatic theorem
, this manner of obtaining a PES is often referred to as the adiabatic approximation and the PES itself is called an adiabatic surface.
In the second step of the BO approximation the nuclear kinetic energy Tn (containing partial derivatives with respect to the components of R) is reintroduced and the Schrödinger equation for the nuclear motion
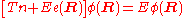
is solved. This second step of the BO approximation involves separation of vibrational, translational, and rotational motions. This can be achieved by application of the Eckart conditions
. The eigenvalue E is the total energy of the molecule, including contributions from electrons, nuclear vibrations, and overall rotation and translation of the molecule.
s." Classically this statement makes sense only if one assumes in addition that the momentum
p of electrons and nuclei is of the same order of magnitude. In that case mnuc >> melec implies p2/(2mnuc) << p2/(2melec). Quantum mechanically it is not unreasonable to assume that the momenta of the electrons and nuclei in a molecule are comparable in magnitude (recall that the corresponding operators do not contain mass and think of the molecule as a box containing the electrons and nuclei and see particle in a box
). Since the kinetic energy is p2/(2m), it follows that, indeed, the kinetic energy of the nuclei in a molecule is usually much smaller than the kinetic energy of the electrons, the mass ratio being on the order of 104).
It is assumed, in accordance with the adiabatic theorem
, that the same electronic state (for instance the electronic ground state) is obtained upon small changes of the nuclear geometry. The method would give a discontinuity (jump) in the PES if electronic state-switching would occur.
This equation is time-independent and stationary wavefunctions for the nuclei are obtained, nevertheless it is traditional to use the word "motion" in this context, although classically motion implies time-dependence.
. To that end the second step of the BO approximation is generalized to a set of coupled eigenvalue equations depending on nuclear coordinates only. Off-diagonal elements in these equations are shown to be nuclear kinetic energy terms.
It will be shown that the BO approximation can be trusted whenever the PESs, obtained from the solution of the electronic Schrödinger equation, are well separated:
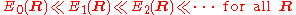 .
.
We start from the exact non-relativistic, time-independent molecular Hamiltonian:
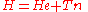
with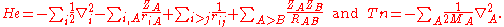
The position vectors
of the electrons and the position vectors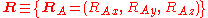 of the nuclei are with respect to a Cartesian inertial frame. Distances between particles are written as
of the nuclei are with respect to a Cartesian inertial frame. Distances between particles are written as 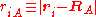 (distance between electron i and nucleus A) and similar definitions hold for
(distance between electron i and nucleus A) and similar definitions hold for  and
and 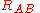 .
.
We assume that the molecule is in a homogeneous
(no external force) and isotropic (no external torque) space. The only interactions are the
Coulomb interactions between the electrons and nuclei. The Hamiltonian is expressed in atomic units
, so that we do not see Planck's constant, the dielectric constant of the vacuum, electronic charge, or electronic mass in this formula. The only constants explicitly entering the formula are ZA and MA—the atomic number and mass of nucleus A.
It is useful to introduce the total nuclear momentum and to rewrite the nuclear kinetic energy operator as follows:

Suppose we have K electronic eigenfunctions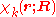 of
of  , that is, we have solved
, that is, we have solved
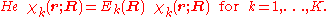
The electronic wave functions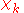 will be taken to be real, which is possible when there are no magnetic or spin interactions. The parametric dependence of the functions
will be taken to be real, which is possible when there are no magnetic or spin interactions. The parametric dependence of the functions 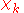 on the nuclear coordinates is indicated by the symbol after the semicolon. This indicates that, although
on the nuclear coordinates is indicated by the symbol after the semicolon. This indicates that, although  is a real-valued function of
is a real-valued function of  , its functional form depends on
, its functional form depends on  .
.
For example, in the molecular-orbital-linear-combination-of-atomic-orbitals (LCAO-MO) approximation, is a molecular orbital (MO) given as a linear expansion of atomic orbitals (AOs). An AO depends visibly on the coordinates of an electron, but the nuclear coordinates are not explicit in the MO. However, upon change of geometry, i.e., change of
is a molecular orbital (MO) given as a linear expansion of atomic orbitals (AOs). An AO depends visibly on the coordinates of an electron, but the nuclear coordinates are not explicit in the MO. However, upon change of geometry, i.e., change of  , the LCAO coefficients obtain different values and we see corresponding changes in the functional form of the MO
, the LCAO coefficients obtain different values and we see corresponding changes in the functional form of the MO  .
.
We will assume that the parametric dependence is continuous and differentiable, so that it is meaningful to consider
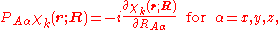
which in general will not be zero.
The total wave function is expanded in terms of
is expanded in terms of 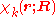 :
: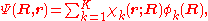
with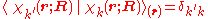
and where the subscript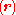 indicates that the integration, implied by the bra-ket notation, is over electronic coordinates only. By definition, the matrix with general element
indicates that the integration, implied by the bra-ket notation, is over electronic coordinates only. By definition, the matrix with general element
is diagonal. After multiplication by the real function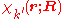 from the left and integration over the electronic coordinates
from the left and integration over the electronic coordinates  the total Schrödinger equation
the total Schrödinger equation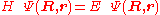
is turned into a set of K coupled eigenvalue equations depending on nuclear coordinates only
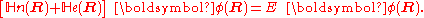
The column vector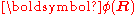 has elements
has elements  . The matrix
. The matrix  is diagonal and the nuclear Hamilton matrix is non-diagonal with the following off-diagonal (vibronic coupling) terms,
is diagonal and the nuclear Hamilton matrix is non-diagonal with the following off-diagonal (vibronic coupling) terms,
The vibronic coupling in this approach is through nuclear kinetic energy terms.
Solution of these coupled equations gives an approximation for energy and wavefunction that goes beyond the Born–Oppenheimer approximation.
Unfortunately, the off-diagonal kinetic energy terms are usually difficult to handle. This is why often a diabatic
transformation is applied, which retains part of the nuclear kinetic energy terms on the diagonal, removes the kinetic energy terms from the off-diagonal and creates coupling terms between the adiabatic PESs on the off-diagonal.
If we can neglect the off-diagonal elements the equations will uncouple and simplify drastically. In order to show when this neglect is justified, we
suppress the coordinates in the notation and write, by applying the Leibniz rule
for differentiation, the matrix elements of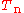 as
as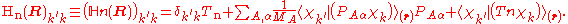
The diagonal ( ) matrix elements
) matrix elements 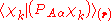 of the operator
of the operator 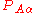 vanish, because this operator is Hermitian and purely imaginary. The off-diagonal matrix elements satisfy
vanish, because this operator is Hermitian and purely imaginary. The off-diagonal matrix elements satisfy

The matrix element in the numerator is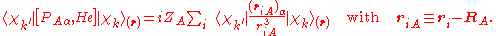
The matrix element of the one-electron operator appearing on the right hand side is finite.
When the two surfaces come close, , the nuclear momentum coupling term becomes large and is no longer negligible. This is the case where
, the nuclear momentum coupling term becomes large and is no longer negligible. This is the case where
the BO approximation breaks down and a coupled set of nuclear motion equations must be considered, instead of the one equation appearing in the second step of the BO approximation.
Conversely, if all surfaces are well separated, all off-diagonal terms can be neglected and hence the whole matrix of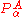 is effectively zero. The third term on the right hand side of the expression for the matrix element of Tn (the Born–Oppenheimer diagonal correction) can approximately be written as the matrix of
is effectively zero. The third term on the right hand side of the expression for the matrix element of Tn (the Born–Oppenheimer diagonal correction) can approximately be written as the matrix of  squared and, accordingly, is then negligible also. Only the first (diagonal) kinetic energy term in this equation survives in the case of well-separated surfaces and a diagonal, uncoupled, set of nuclear motion equations results,
squared and, accordingly, is then negligible also. Only the first (diagonal) kinetic energy term in this equation survives in the case of well-separated surfaces and a diagonal, uncoupled, set of nuclear motion equations results,
which are the normal second-step of the BO equations discussed above.
We reiterate that when two or more potential energy surfaces approach each other, or even cross, the Born–Oppenheimer
approximation breaks down and one must fall back on the coupled equations. Usually one
invokes then the diabatic
approximation.
very hard to follow, in contrast to the explanation and derivation above. Moreover, knowing that the proper separation of vibrations and rotations was not achieved in this paper, but only eight years later [] (see Eckart conditions
), there is little need to understand the work by Born and Oppenheimer, however famous it may be. Although the article still collects many citations each year, it is safe to say that it is not read anymore (except perhaps by historians of science).
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
, the computation of the energy and wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
of an average-size molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
is a formidable task that is alleviated by the Born–Oppenheimer (BO) approximation, named after Max Born
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
and J. Robert Oppenheimer. For instance the benzene
Benzene
Benzene is an organic chemical compound. It is composed of 6 carbon atoms in a ring, with 1 hydrogen atom attached to each carbon atom, with the molecular formula C6H6....
molecule consists of 12 nuclei and 42 electrons. The time independent Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, which must be solved to obtain the energy and molecular wavefunction of this molecule, is a partial differential eigenvalue equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
in 162 variables—the spatial coordinates of the electrons and the nuclei. The BO approximation makes it possible to compute the wavefunction in two less complicated consecutive steps. This approximation was proposed in 1927, in the early period of quantum mechanics, by Born and Oppenheimer and is still indispensable in quantum chemistry.
In basic terms, it allows the wavefunction of a molecule to be broken into its electronic and nuclear (vibrational, rotational) components.
In the first step of the BO approximation the electronic Schrödinger equation is solved, yielding the wavefunction
 depending on electrons only. For benzene this wavefunction depends on 126 electronic coordinates. During this solution the nuclei are fixed in a certain configuration, very often the equilibrium configuration. If the effects of the quantum mechanical nuclear motion are to be studied, for instance because a vibrational spectrum
depending on electrons only. For benzene this wavefunction depends on 126 electronic coordinates. During this solution the nuclei are fixed in a certain configuration, very often the equilibrium configuration. If the effects of the quantum mechanical nuclear motion are to be studied, for instance because a vibrational spectrumMolecular vibration
A molecular vibration occurs when atoms in a molecule are in periodic motion while the molecule as a whole has constant translational and rotational motion...
is required, this electronic computation must be in nuclear coordinates. In the second step of the BO approximation this function serves as a potential in a Schrödinger equation containing only the nuclei—for benzene an equation in 36 variables.
The success of the BO approximation is due to the high ratio between nuclear and electronic masses. The approximation is an important tool of quantum chemistry; without it only the lightest molecule, H2, could be handled, and all computations of molecular wavefunctions for larger molecules make use of it. Even in the cases where the BO approximation breaks down, it is used as a point of departure for the computations.
The electronic energies, constituting the nuclear potential, consist of kinetic energies, interelectronic repulsions and electron–nuclear attractions. In a handwaving
Handwaving
Handwaving is a pejorative label applied to the action of displaying the appearance of doing something, when actually doing little, or nothing. For example, it is applied to debate techniques that involve logical fallacies. It is also used in working situations where productive work is expected,...
manner the nuclear potential is taken to be an averaged electron–nuclear attraction.
The BO approximation follows from the inertia of electrons being considered to be negligible in comparison to the atom to which they are bound.
Short description
The BornMax Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
–Oppenheimer
Robert Oppenheimer
Julius Robert Oppenheimer was an American theoretical physicist and professor of physics at the University of California, Berkeley. Along with Enrico Fermi, he is often called the "father of the atomic bomb" for his role in the Manhattan Project, the World War II project that developed the first...
(BO) approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
is ubiquitous in quantum chemical
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
calculations of molecular wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s. It consists of two steps.
In the first step the nuclear kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
is neglected, that is, the corresponding operator Tn is subtracted from the total molecular Hamiltonian
Molecular Hamiltonian
In atomic, molecular, and optical physics as well as in quantum chemistry, molecular Hamiltonian is the name given to the Hamiltonian representing the energy of the electrons and nuclei in a molecule...
. In the remaining electronic Hamiltonian He the nuclear positions enter as parameters. The electron–nucleus interactions are not removed and the electrons still "feel" the Coulomb potential of the nuclei clamped at certain positions in space. (This first step of the BO approximation is therefore often referred to as the clamped nuclei approximation.)
The electronic Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
is solved (out of necessity, approximately). The quantity r stands for all electronic coordinates and R for all nuclear coordinates. The electronic energy eigenvalue Ee depends on the chosen positions R of the nuclei. Varying these positions R in small steps and repeatedly solving the electronic Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, one obtains Ee as a function of R. This is the potential energy surface
Potential energy surface
A potential energy surface is generally used within the adiabatic or Born–Oppenheimer approximation in quantum mechanics and statistical mechanics to model chemical reactions and interactions in simple chemical and physical systems...
(PES): Ee(R) . Because this procedure of recomputing the electronic wave functions as a function of an infinitesimally changing nuclear geometry is reminiscent of the conditions for the adiabatic theorem
Adiabatic theorem
The adiabatic theorem is an important concept in quantum mechanics. Its original form, due to Max Born and Vladimir Fock , can be stated as follows:...
, this manner of obtaining a PES is often referred to as the adiabatic approximation and the PES itself is called an adiabatic surface.
In the second step of the BO approximation the nuclear kinetic energy Tn (containing partial derivatives with respect to the components of R) is reintroduced and the Schrödinger equation for the nuclear motion
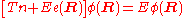
is solved. This second step of the BO approximation involves separation of vibrational, translational, and rotational motions. This can be achieved by application of the Eckart conditions
Eckart conditions
The Eckart conditions, named after Carl Eckart, sometimes referred to as Sayvetz conditions, simplify the nuclear motion Schrödinger equation that arises in the second step of the Born-Oppenheimer approximation. The Eckart conditions allow to a large extent the separation of the external ...
. The eigenvalue E is the total energy of the molecule, including contributions from electrons, nuclear vibrations, and overall rotation and translation of the molecule.
Footnotes
This step is often justified by stating that "the heavy nuclei move more slowly than the light electronElectron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s." Classically this statement makes sense only if one assumes in addition that the momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
p of electrons and nuclei is of the same order of magnitude. In that case mnuc >> melec implies p2/(2mnuc) << p2/(2melec). Quantum mechanically it is not unreasonable to assume that the momenta of the electrons and nuclei in a molecule are comparable in magnitude (recall that the corresponding operators do not contain mass and think of the molecule as a box containing the electrons and nuclei and see particle in a box
Particle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
). Since the kinetic energy is p2/(2m), it follows that, indeed, the kinetic energy of the nuclei in a molecule is usually much smaller than the kinetic energy of the electrons, the mass ratio being on the order of 104).
It is assumed, in accordance with the adiabatic theorem
Adiabatic theorem
The adiabatic theorem is an important concept in quantum mechanics. Its original form, due to Max Born and Vladimir Fock , can be stated as follows:...
, that the same electronic state (for instance the electronic ground state) is obtained upon small changes of the nuclear geometry. The method would give a discontinuity (jump) in the PES if electronic state-switching would occur.
This equation is time-independent and stationary wavefunctions for the nuclei are obtained, nevertheless it is traditional to use the word "motion" in this context, although classically motion implies time-dependence.
Derivation of the Born–Oppenheimer approximation
It will be discussed how the BO approximation may be derived and under which conditions it is applicable. At the same time we will show how the BO approximation may be improved by including vibronic couplingVibronic coupling
In theoretical chemistry, the vibronic coupling terms, , are proportional to the interaction between electronic and nuclear motions of molecules. The term "vibronic" originates from the concatenation of the terms "vibrational" and "electronic"...
. To that end the second step of the BO approximation is generalized to a set of coupled eigenvalue equations depending on nuclear coordinates only. Off-diagonal elements in these equations are shown to be nuclear kinetic energy terms.
It will be shown that the BO approximation can be trusted whenever the PESs, obtained from the solution of the electronic Schrödinger equation, are well separated:
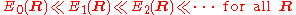 .
.We start from the exact non-relativistic, time-independent molecular Hamiltonian:
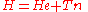
with
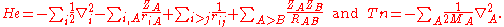
The position vectors

of the electrons and the position vectors
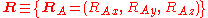 of the nuclei are with respect to a Cartesian inertial frame. Distances between particles are written as
of the nuclei are with respect to a Cartesian inertial frame. Distances between particles are written as 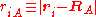 (distance between electron i and nucleus A) and similar definitions hold for
(distance between electron i and nucleus A) and similar definitions hold for  and
and 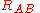 .
.We assume that the molecule is in a homogeneous
(no external force) and isotropic (no external torque) space. The only interactions are the
Coulomb interactions between the electrons and nuclei. The Hamiltonian is expressed in atomic units
Atomic units
Atomic units form a system of natural units which is especially convenient for atomic physics calculations. There are two different kinds of atomic units, which one might name Hartree atomic units and Rydberg atomic units, which differ in the choice of the unit of mass and charge. This article...
, so that we do not see Planck's constant, the dielectric constant of the vacuum, electronic charge, or electronic mass in this formula. The only constants explicitly entering the formula are ZA and MA—the atomic number and mass of nucleus A.
It is useful to introduce the total nuclear momentum and to rewrite the nuclear kinetic energy operator as follows:

Suppose we have K electronic eigenfunctions
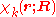 of
of  , that is, we have solved
, that is, we have solved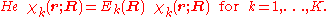
The electronic wave functions
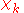 will be taken to be real, which is possible when there are no magnetic or spin interactions. The parametric dependence of the functions
will be taken to be real, which is possible when there are no magnetic or spin interactions. The parametric dependence of the functions 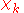 on the nuclear coordinates is indicated by the symbol after the semicolon. This indicates that, although
on the nuclear coordinates is indicated by the symbol after the semicolon. This indicates that, although  is a real-valued function of
is a real-valued function of  , its functional form depends on
, its functional form depends on  .
.For example, in the molecular-orbital-linear-combination-of-atomic-orbitals (LCAO-MO) approximation,
 is a molecular orbital (MO) given as a linear expansion of atomic orbitals (AOs). An AO depends visibly on the coordinates of an electron, but the nuclear coordinates are not explicit in the MO. However, upon change of geometry, i.e., change of
is a molecular orbital (MO) given as a linear expansion of atomic orbitals (AOs). An AO depends visibly on the coordinates of an electron, but the nuclear coordinates are not explicit in the MO. However, upon change of geometry, i.e., change of  , the LCAO coefficients obtain different values and we see corresponding changes in the functional form of the MO
, the LCAO coefficients obtain different values and we see corresponding changes in the functional form of the MO  .
.We will assume that the parametric dependence is continuous and differentiable, so that it is meaningful to consider
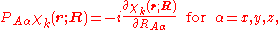
which in general will not be zero.
The total wave function
 is expanded in terms of
is expanded in terms of 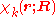 :
: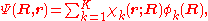
with
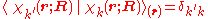
and where the subscript
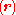 indicates that the integration, implied by the bra-ket notation, is over electronic coordinates only. By definition, the matrix with general element
indicates that the integration, implied by the bra-ket notation, is over electronic coordinates only. By definition, the matrix with general element
is diagonal. After multiplication by the real function
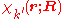 from the left and integration over the electronic coordinates
from the left and integration over the electronic coordinates  the total Schrödinger equation
the total Schrödinger equation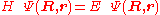
is turned into a set of K coupled eigenvalue equations depending on nuclear coordinates only
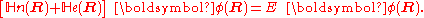
The column vector
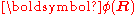 has elements
has elements  . The matrix
. The matrix  is diagonal and the nuclear Hamilton matrix is non-diagonal with the following off-diagonal (vibronic coupling) terms,
is diagonal and the nuclear Hamilton matrix is non-diagonal with the following off-diagonal (vibronic coupling) terms,
The vibronic coupling in this approach is through nuclear kinetic energy terms.
Solution of these coupled equations gives an approximation for energy and wavefunction that goes beyond the Born–Oppenheimer approximation.
Unfortunately, the off-diagonal kinetic energy terms are usually difficult to handle. This is why often a diabatic
Diabatic
A diabatic process is one in which heat transfer takes place, which is the opposite of an adiabatic process. In quantum chemistry, the potential energy surfaces are obtained within the adiabatic or Born-Oppenheimer approximation...
transformation is applied, which retains part of the nuclear kinetic energy terms on the diagonal, removes the kinetic energy terms from the off-diagonal and creates coupling terms between the adiabatic PESs on the off-diagonal.
If we can neglect the off-diagonal elements the equations will uncouple and simplify drastically. In order to show when this neglect is justified, we
suppress the coordinates in the notation and write, by applying the Leibniz rule
Leibniz rule (generalized product rule)
In calculus, the general Leibniz rule, named after Gottfried Leibniz, generalizes the product rule. It states that if f and g are n-times differentiable functions, then the nth derivative of the product fg is given by...
for differentiation, the matrix elements of
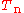 as
as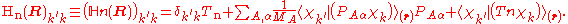
The diagonal (
 ) matrix elements
) matrix elements 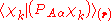 of the operator
of the operator 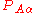 vanish, because this operator is Hermitian and purely imaginary. The off-diagonal matrix elements satisfy
vanish, because this operator is Hermitian and purely imaginary. The off-diagonal matrix elements satisfy
The matrix element in the numerator is
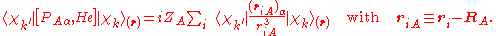
The matrix element of the one-electron operator appearing on the right hand side is finite.
When the two surfaces come close,
 , the nuclear momentum coupling term becomes large and is no longer negligible. This is the case where
, the nuclear momentum coupling term becomes large and is no longer negligible. This is the case wherethe BO approximation breaks down and a coupled set of nuclear motion equations must be considered, instead of the one equation appearing in the second step of the BO approximation.
Conversely, if all surfaces are well separated, all off-diagonal terms can be neglected and hence the whole matrix of
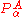 is effectively zero. The third term on the right hand side of the expression for the matrix element of Tn (the Born–Oppenheimer diagonal correction) can approximately be written as the matrix of
is effectively zero. The third term on the right hand side of the expression for the matrix element of Tn (the Born–Oppenheimer diagonal correction) can approximately be written as the matrix of  squared and, accordingly, is then negligible also. Only the first (diagonal) kinetic energy term in this equation survives in the case of well-separated surfaces and a diagonal, uncoupled, set of nuclear motion equations results,
squared and, accordingly, is then negligible also. Only the first (diagonal) kinetic energy term in this equation survives in the case of well-separated surfaces and a diagonal, uncoupled, set of nuclear motion equations results,
which are the normal second-step of the BO equations discussed above.
We reiterate that when two or more potential energy surfaces approach each other, or even cross, the Born–Oppenheimer
approximation breaks down and one must fall back on the coupled equations. Usually one
invokes then the diabatic
Diabatic
A diabatic process is one in which heat transfer takes place, which is the opposite of an adiabatic process. In quantum chemistry, the potential energy surfaces are obtained within the adiabatic or Born-Oppenheimer approximation...
approximation.
Historical note
Born and Oppenheimer wrote the paper: This paper describes the separation of electronic motion, nuclear vibrations, and molecular rotation. However, in the original paper the presentation of the BO approximation is well hidden in Taylor expansions (in terms of internal and external nuclear coordinates) of (i) electronic wave functions, (ii) potential energy surfaces and (iii) nuclear kinetic energy terms. Internal coordinates are the relative positions of the nuclei in the molecular equilibrium and their displacements (vibrations) from equilibrium. External coordinates are the position of the center of mass and the orientation of the molecule. The Taylor expansions complicate the theory and make the derivationsvery hard to follow, in contrast to the explanation and derivation above. Moreover, knowing that the proper separation of vibrations and rotations was not achieved in this paper, but only eight years later [] (see Eckart conditions
Eckart conditions
The Eckart conditions, named after Carl Eckart, sometimes referred to as Sayvetz conditions, simplify the nuclear motion Schrödinger equation that arises in the second step of the Born-Oppenheimer approximation. The Eckart conditions allow to a large extent the separation of the external ...
), there is little need to understand the work by Born and Oppenheimer, however famous it may be. Although the article still collects many citations each year, it is safe to say that it is not read anymore (except perhaps by historians of science).
See also
- Born–Huang approximation
- Adiabatic process (quantum mechanics)
- Franck–Condon principle
- Adiabatic ionizationAdiabatic ionizationAdiabatic ionization is a form of ionization in which an electron is removed from or added to an atom or molecule in its lowest energy state to form an ion in its lowest energy state....
External links
Resources related to the Born–Oppenheimer approximation:- The Born–Oppenheimer approximation, a section from Peter Haynes' doctoral thesis