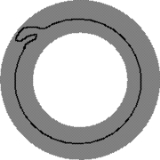
Boundary parallel
Encyclopedia
In mathematics
, a closed
n-manifold
N embedded
in an (n + 1)-manifold M is boundary parallel (or ∂-parallel, or peripheral) if there is an isotopy of N onto a boundary
component
of M.
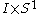 . Let π denote the projection map
. Let π denote the projection map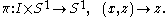
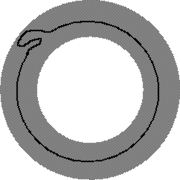
If a circle S is embedded into the annulus so that π restricted to S is a bijection
, then S is boundary parallel. (The converse
is not true.)
If, on the other hand, a circle S is embedded into the annulus so that π restricted to S is not surjective, then S is not boundary parallel. (Again, the converse is not true.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a closed
Closed
Closed may refer to:Math* Closure * Closed manifold* Closed orbits* Closed set* Closed differential form* Closed map, a function that is closed.Other* Cloister, a closed walkway* Closed-circuit television...
n-manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
N embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in an (n + 1)-manifold M is boundary parallel (or ∂-parallel, or peripheral) if there is an isotopy of N onto a boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
of M.
An example
Consider the annulusAnnulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
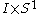 . Let π denote the projection map
. Let π denote the projection map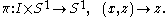
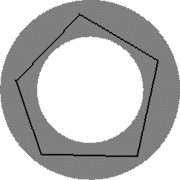
If a circle S is embedded into the annulus so that π restricted to S is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
, then S is boundary parallel. (The converse
Converse (logic)
In logic, the converse of a categorical or implicational statement is the result of reversing its two parts. For the implication P → Q, the converse is Q → P. For the categorical proposition All S is P, the converse is All P is S. In neither case does the converse necessarily follow from...
is not true.)
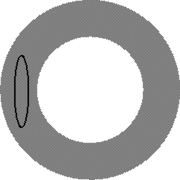
If, on the other hand, a circle S is embedded into the annulus so that π restricted to S is not surjective, then S is not boundary parallel. (Again, the converse is not true.)




