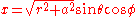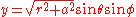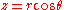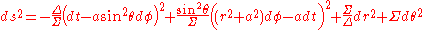Boyer-Lindquist coordinates
Encyclopedia
A generalization of the coordinates used for the metric of a Schwarzschild black hole that can be used to express the metric of a Kerr black hole.
The coordinate transformation from Boyer–Lindquist coordinates r,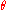 ,
,  to cartesian coordinates x, y, z is given by
to cartesian coordinates x, y, z is given by
The line element for a black hole with mass , angular momentum
, angular momentum  , and charge
, and charge  in Boyer–Lindquist coordinates and natural units
in Boyer–Lindquist coordinates and natural units
(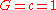 ) is
) is
where
Note that in natural units ,
,  , and
, and  all have units of length. This line element describes the Kerr-Newman metric
all have units of length. This line element describes the Kerr-Newman metric
.
The Hamiltonian for test particle motion in Kerr spacetime was separable in Boyer–Lindquist coordinates. Using Hamilton-Jacobi theory one can derive a fourth constant of the motion known as Carter's constant
.
The coordinate transformation from Boyer–Lindquist coordinates r,
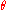 ,
,  to cartesian coordinates x, y, z is given by
to cartesian coordinates x, y, z is given by
The line element for a black hole with mass
 , angular momentum
, angular momentum  , and charge
, and charge  in Boyer–Lindquist coordinates and natural units
in Boyer–Lindquist coordinates and natural unitsNatural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
(
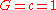 ) is
) iswhere
-


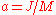 , the angular momentum per unit mass of the black hole
, the angular momentum per unit mass of the black hole
Note that in natural units
 ,
,  , and
, and  all have units of length. This line element describes the Kerr-Newman metric
all have units of length. This line element describes the Kerr-Newman metricKerr-Newman metric
The Kerr–Newman metric is a solution of the Einstein–Maxwell equations in general relativity, describing the spacetime geometry in the region surrounding a charged, rotating mass. It is assumed that the cosmological constant equals zero...
.
The Hamiltonian for test particle motion in Kerr spacetime was separable in Boyer–Lindquist coordinates. Using Hamilton-Jacobi theory one can derive a fourth constant of the motion known as Carter's constant
Carter constant
The Carter constant is a conserved quantity for motion around black holes in the general relativistic formulation of gravity. Carter's constant was derived for a spinning, charged black hole by Australian theoretical physicist Brandon Carter in 1968...
.