Brauer algebra
Encyclopedia
In mathematics, a Brauer algebra is an algebra introduced by used in the representation theory
of the orthogonal group
. It plays the same role that the symmetric group
does for the representation theory of the general linear group
in Schur–Weyl duality
.
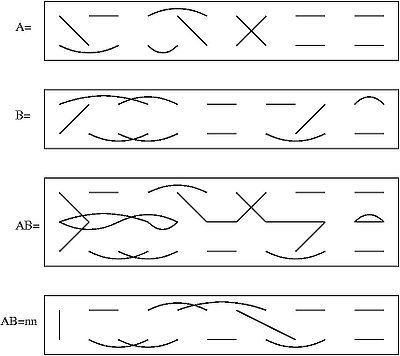The Brauer algebra depends on the choice of a positive integer n and a number d (which in practice is often the dimension of the fundamental representation
of an orthogonal group Od). The Brauer algebra has dimension (2n)!/2nn! = (2n − 1)(2n − 3) ··· 5·3·1 and has a basis consisting of all pairings on a set of 2n elements X1, ..., Xn, Y1, ..., Yn (that is, all perfect matchings of a complete graph
K2n: any two of the 2n elements may be matched to each other, regardless of their symbols). The elements Xi are usually written in a row, with the elements Yi beneath them. The product of two basis elements A and B is obtained by "splicing" A to B by placing A on top of B and then replacing every loop by a factor of n, as in the diagram.
the Brauer algebra has a natural action on the space of polynomials on Vn commuting with the action of the orthogonal group.
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
. It plays the same role that the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
does for the representation theory of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
in Schur–Weyl duality
Schur–Weyl duality
Schur–Weyl duality is a mathematical theorem in representation theory that relates irreducible finite-dimensional representations of the general linear and symmetric groups...
.
Definition
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
of an orthogonal group Od). The Brauer algebra has dimension (2n)!/2nn! = (2n − 1)(2n − 3) ··· 5·3·1 and has a basis consisting of all pairings on a set of 2n elements X1, ..., Xn, Y1, ..., Yn (that is, all perfect matchings of a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K2n: any two of the 2n elements may be matched to each other, regardless of their symbols). The elements Xi are usually written in a row, with the elements Yi beneath them. The product of two basis elements A and B is obtained by "splicing" A to B by placing A on top of B and then replacing every loop by a factor of n, as in the diagram.
The orthogonal group
If Od(R) is the orthogonal group acing on V = Rd, thenthe Brauer algebra has a natural action on the space of polynomials on Vn commuting with the action of the orthogonal group.