
Cayley–Klein metric
Encyclopedia
In mathematics, a Cayley–Klein metric is a metric
on the complement of a fixed quadric in projective space
defined using a cross-ratio
. The first example was given by , and they were studied further by .
The Cayley–Klein metric can be used to define the distance in the Cayley–Klein model of hyperbolic geometry
.
The Hilbert metric
of a convex set is defined in a similar way.
If p and q are 2 points then the line through p and q intersects the quadric Q in 2 further points a and b. The Cayley–Klein distance d(p,q) from p to q is proportional to the logarithm of the cross-ratio
: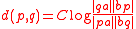
for some fixed constant C.
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on the complement of a fixed quadric in projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
defined using a cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
. The first example was given by , and they were studied further by .
The Cayley–Klein metric can be used to define the distance in the Cayley–Klein model of hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
.
The Hilbert metric
Hilbert metric
In mathematics, the Hilbert metric, also known as the Hilbert projective metric, is an explicitly defined distance function on a bounded convex subset of the n-dimensional Euclidean space Rn...
of a convex set is defined in a similar way.
Definition
Suppose that Q is a fixed quadric in projective space.If p and q are 2 points then the line through p and q intersects the quadric Q in 2 further points a and b. The Cayley–Klein distance d(p,q) from p to q is proportional to the logarithm of the cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
:
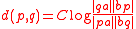
for some fixed constant C.

