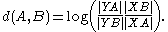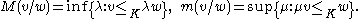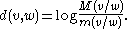Hilbert metric
Encyclopedia
In mathematics
, the Hilbert metric, also known as the Hilbert projective metric, is an explicitly defined distance function
on a bounded convex subset
of the n-dimensional Euclidean space
Rn. It was introduced by as a generalization of the Cayley's formula for the distance in the Cayley–Klein model
of hyperbolic geometry
, where the convex set is the n-dimensional open unit ball. Hilbert's metric has been applied to Perron–Frobenius theory
and to constructing Gromov hyperbolic spaces.
open
domain in a Euclidean space
that does not contain a line. Given two distinct points A and B of Ω, let X and Y be the points at which the straight line AB intersects the boundary of Ω, where the order of the points is X, A, B, Y. Then the Hilbert distance d(A, B) is the logarithm
of the cross-ratio
of this quadruple of points:
The function d is extended to all pairs of points by letting d(A, A) = 0 and defines a metric
on Ω. If one of the points A and B lies on the boundary of Ω then d can be formally defined to be +∞, corresponding to a limiting case of the above formula
when one of the denominators is zero.
A variant of this construction arises for a closed
convex cone
K in a Banach space
V (possibly, infinite-dimensional). In addition, the cone K is assumed to be pointed, i.e. K ∩ (−K) = {0} and thus K determines a partial order
on V. Given any vectors v and w in K \ {0}, one first defines
The Hilbert pseudometric on K\{0} is then defined by the formula
It is invariant under the rescaling of v and w by positive constants and so descends to a metric on the space of rays of K, which is interpreted as the projectivization of K (in order for d to be finite, one needs to restrict to the interior of K). Moreover, if K ⊂ R × V is the cone over a convex set Ω,
then the space of rays of K is canonically isomorphic to Ω. If v and w are vectors in rays in K corresponding to the points A, B ∈ Ω then these two formulas for d yield the same value of the distance.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hilbert metric, also known as the Hilbert projective metric, is an explicitly defined distance function
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on a bounded convex subset
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
of the n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn. It was introduced by as a generalization of the Cayley's formula for the distance in the Cayley–Klein model
Klein model
In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of n-dimensional hyperbolic geometry in which points are represented by the points in the interior of the n-dimensional unit ball and lines are represented by the...
of hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, where the convex set is the n-dimensional open unit ball. Hilbert's metric has been applied to Perron–Frobenius theory
Perron–Frobenius theorem
In linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
and to constructing Gromov hyperbolic spaces.
Definition
Let Ω be a convexConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
domain in a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
that does not contain a line. Given two distinct points A and B of Ω, let X and Y be the points at which the straight line AB intersects the boundary of Ω, where the order of the points is X, A, B, Y. Then the Hilbert distance d(A, B) is the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of the cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
of this quadruple of points:
The function d is extended to all pairs of points by letting d(A, A) = 0 and defines a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on Ω. If one of the points A and B lies on the boundary of Ω then d can be formally defined to be +∞, corresponding to a limiting case of the above formula
when one of the denominators is zero.
A variant of this construction arises for a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
K in a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
V (possibly, infinite-dimensional). In addition, the cone K is assumed to be pointed, i.e. K ∩ (−K) = {0} and thus K determines a partial order
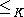on V. Given any vectors v and w in K \ {0}, one first defines
The Hilbert pseudometric on K\{0} is then defined by the formula
It is invariant under the rescaling of v and w by positive constants and so descends to a metric on the space of rays of K, which is interpreted as the projectivization of K (in order for d to be finite, one needs to restrict to the interior of K). Moreover, if K ⊂ R × V is the cone over a convex set Ω,
then the space of rays of K is canonically isomorphic to Ω. If v and w are vectors in rays in K corresponding to the points A, B ∈ Ω then these two formulas for d yield the same value of the distance.
Examples
- In the case where the domain Ω is a unit ball in Rn, the formula for d coincides with the expression for the distance between points in the Cayley–Klein modelKlein modelIn geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of n-dimensional hyperbolic geometry in which points are represented by the points in the interior of the n-dimensional unit ball and lines are represented by the...
of hyperbolic geometryHyperbolic geometryIn mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, up to a multiplicative constant.
- If the cone K is the positive orthantOrthantIn geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....
in Rn then the induced metric on the projectivization of K is often called simply Hilbert's projective metric. This cone corresponds to a domain Ω which is a regular simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
of dimension n − 1.
Motivation and applications
- Hilbert introduced his metric in order to construct an axiomatic metric geometry in which there exist triangles ABC whose vertices A, B, C are not collinearLine (geometry)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, yet one of the sides is equal to the sum of the other two — it follows that the shortest path connecting two points is not unique in this geometry. In particular, this happens when the convex set Ω is a Euclidean triangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
and the straight line extensions of the segments AB, BC, AC do not meet the interior of one of the sides of Ω.
- Garrett BirkhoffGarrett BirkhoffGarrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
used Hilbert's metric and the Banach contraction principle to rederive the Perron–Frobenius theoremPerron–Frobenius theoremIn linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
in finite-dimensional linear algebra and its analogues for integral operators with positive kernels.
- Generalizing earlier results of Anders Karlsson and Guennadi Noskov, Yves Benoist determined a system of necessary and sufficient conditions for a bounded convex domain in Rn, endowed with its Hilbert metric, to be a Gromov hyperbolic space.