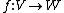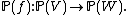Projectivization
Encyclopedia
In mathematics
, projectivization is a procedure which associates to a non-zero vector space
V its associated projective space
 , whose elements are one-dimensional subspace
, whose elements are one-dimensional subspace
s of V. More generally, any subset S of V closed under scalar multiplication defines a subset of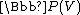 formed by the lines contained in S and called the projectivization of S.
formed by the lines contained in S and called the projectivization of S.
K into the projective space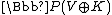 of the same dimension. To every vector v of V, it associates the line spanned by the vector (v,1) of V⊕K.
of the same dimension. To every vector v of V, it associates the line spanned by the vector (v,1) of V⊕K.
, there is a procedure that associates a projective variety Proj S with a graded commutative algebra
S (under some technical restrictions on S). If S is the algebra of polynomial functions on a vector space V then Proj S is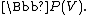 This Proj construction
This Proj construction
gives rise to a contravariant functor from the category of graded commutative rings and surjective graded maps to the category of projective schemes
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, projectivization is a procedure which associates to a non-zero vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V its associated projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
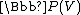 , whose elements are one-dimensional subspace
, whose elements are one-dimensional subspaceSubspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
s of V. More generally, any subset S of V closed under scalar multiplication defines a subset of
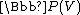 formed by the lines contained in S and called the projectivization of S.
formed by the lines contained in S and called the projectivization of S.Properties
- Projectivization is a special case of the factorizationQuotient spaceIn topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
by a group actionGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
: the projective space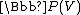 is the quotient of the open set V\{0} of nonzero vectors by the action of the multiplicative group of the base field by scalar transformations. The dimension of
is the quotient of the open set V\{0} of nonzero vectors by the action of the multiplicative group of the base field by scalar transformations. The dimension of 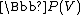 in the sense of algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
in the sense of algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
is one less than the dimension of the vector space V.
- Projectivization is functorialFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
with respect to injective linear maps: if
- is a linear map with trivial kernel then f defines an algebraic map of the corresponding projective spaces,
- In particular, the general linear groupGeneral linear groupIn mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(V) acts on the projective space by automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
by automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s.
Projective completion
A related procedure embeds a vector space V over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K into the projective space
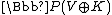 of the same dimension. To every vector v of V, it associates the line spanned by the vector (v,1) of V⊕K.
of the same dimension. To every vector v of V, it associates the line spanned by the vector (v,1) of V⊕K.Generalization
In algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, there is a procedure that associates a projective variety Proj S with a graded commutative algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
S (under some technical restrictions on S). If S is the algebra of polynomial functions on a vector space V then Proj S is
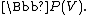 This Proj construction
This Proj constructionProj construction
In algebraic geometry, Proj is a construction analogous to the spectrum-of-a-ring construction of affine schemes, which produces objects with the typical properties of projective spaces and projective varieties...
gives rise to a contravariant functor from the category of graded commutative rings and surjective graded maps to the category of projective schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
.