
Center vortex
Encyclopedia
Center vortices are line-like topological defect
s that exist in the vacuum
of Yang–Mills theory and QCD
. They seem to play an important role in the confinement of quark
s.
elements of the gauge group. In the case of SU(N) gauge theories, these are the constant matrices: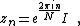
where I is the unit matrix. These elements form the abelian subgroup ZN
. Under such center elements, quarks transform as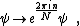
while gluon
s are invariant. This means that, if quarks are free (like in the deconfined phase
), the center symmetry will be broken. Restoration of the center symmetry will imply confinement. 't Hooft first put this on a more rigorous footing.
The two phases in the theory can be distinguished based on the behavior of the vortices. When considering a certain Wilson loop
, if the vortices are generally long, most vortices will only pierce the surface within the Wilson loop once. Furthermore the number of vortices piercing this surface will grow in proportion to the area of the surface. Due to the vortices suppressing the value of the vacuum expectation value
of the Wilson loop, this will lead to an area-law, i.e. the Wilson loop W(C) behaves like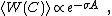
where A is the area spanned by the loop. The constant σ is called the string tension. This behavior is typical of confinement. However, when considering a regime where vortices are generally short — i.e. they form small loops — they will usually pierce the surface of the Wislon loop twice in opposite directions, thus leading to the two contributions canceling. Only vortex loops near the Wilson loop itself will pierce it once, thus leading to a contribution scaling like the perimeter: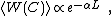
with L the length of the Wilson loop, and α some constant. This behavior signals there is no confinement.
In lattice simulations
this behavior is indeed seen. At low temperatures (where there is confinement) vortices form large, complex clusters and percolate through space. At higher temperatures (above the deconfinement phase transition) vortices form small loops. Furthermore it has been seen that the string tension almost drops to zero when center vortices are removed from the simulation. At the other hand, the string tension remains approximately unchanged when removing everything except for the center vortices. This clearly shows the close relation between center vortices and confinement. Aside from this it has also been shown in simulations that the vortices have a finite density in the continuum limit (meaning they are not a lattice artifact, but they do exist in reality), and that they are also linked with chiral symmetry breaking and topological charge.
One subtlety concerns the string tension at intermediate range and in the large-N limit
. According to the center vortex picture, the string tension should depend on the way the matter fields transform under the center, i.e. their so-called N-ality. This seems to be correct for the large-distance string tension, but at smaller distances the string tension is instead proportional to the quadratic Casimir
of the representation — so-called Casimir scaling. This has been explained by domain formation around center vortices. In the large-N limit, this Casimir scaling goes all the way to large distances.
π1 which should be considered. Also mark that a theory like G2 gauge theory does not have a long-range string tension, which is consistent with the center vortex picture. In this theory, gluons can screen quarks, leading to color singlet states with the quantum number of quarks. Casimir scaling is, however, still present at intermediate ranges, i.e. before string breaking occurs. This can be explained by domain formation.
Topological defect
In mathematics and physics, a topological soliton or a topological defect is a solution of a system of partial differential equations or of a quantum field theory homotopically distinct from the vacuum solution; it can be proven to exist because the boundary conditions entail the existence of...
s that exist in the vacuum
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
of Yang–Mills theory and QCD
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
. They seem to play an important role in the confinement of quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s.
In SU(N) theories
Center vortices are line-like topological defect that carry a gauge charge equal to one of the centerCenter (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
elements of the gauge group. In the case of SU(N) gauge theories, these are the constant matrices:
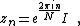
where I is the unit matrix. These elements form the abelian subgroup ZN
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
. Under such center elements, quarks transform as
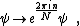
while gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s are invariant. This means that, if quarks are free (like in the deconfined phase
Deconfinement
In physics, deconfinement is the property of a phase in which certain particles are allowed to exist as free excitations, rather than only within bound states...
), the center symmetry will be broken. Restoration of the center symmetry will imply confinement. 't Hooft first put this on a more rigorous footing.
The two phases in the theory can be distinguished based on the behavior of the vortices. When considering a certain Wilson loop
Wilson loop
In gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...
, if the vortices are generally long, most vortices will only pierce the surface within the Wilson loop once. Furthermore the number of vortices piercing this surface will grow in proportion to the area of the surface. Due to the vortices suppressing the value of the vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of the Wilson loop, this will lead to an area-law, i.e. the Wilson loop W(C) behaves like
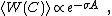
where A is the area spanned by the loop. The constant σ is called the string tension. This behavior is typical of confinement. However, when considering a regime where vortices are generally short — i.e. they form small loops — they will usually pierce the surface of the Wislon loop twice in opposite directions, thus leading to the two contributions canceling. Only vortex loops near the Wilson loop itself will pierce it once, thus leading to a contribution scaling like the perimeter:
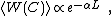
with L the length of the Wilson loop, and α some constant. This behavior signals there is no confinement.
In lattice simulations
Lattice gauge theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice. Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum electrodynamics, quantum chromodynamics and the Standard...
this behavior is indeed seen. At low temperatures (where there is confinement) vortices form large, complex clusters and percolate through space. At higher temperatures (above the deconfinement phase transition) vortices form small loops. Furthermore it has been seen that the string tension almost drops to zero when center vortices are removed from the simulation. At the other hand, the string tension remains approximately unchanged when removing everything except for the center vortices. This clearly shows the close relation between center vortices and confinement. Aside from this it has also been shown in simulations that the vortices have a finite density in the continuum limit (meaning they are not a lattice artifact, but they do exist in reality), and that they are also linked with chiral symmetry breaking and topological charge.
One subtlety concerns the string tension at intermediate range and in the large-N limit
1/N expansion
In quantum field theory and statistical mechanics, the 1/N expansion is a particular perturbative analysis of quantum field theories with an internal symmetry group such as SO or SU...
. According to the center vortex picture, the string tension should depend on the way the matter fields transform under the center, i.e. their so-called N-ality. This seems to be correct for the large-distance string tension, but at smaller distances the string tension is instead proportional to the quadratic Casimir
Casimir invariant
In mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...
of the representation — so-called Casimir scaling. This has been explained by domain formation around center vortices. In the large-N limit, this Casimir scaling goes all the way to large distances.
In gauge theories with trivial center
A gauge group like SO(3) has a trivial center, but SO(3) gauge theory is expected to be identical to SU(2) gauge theory. This discrepancy is due to the fact that, rather than the center, it is really the homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
π1 which should be considered. Also mark that a theory like G2 gauge theory does not have a long-range string tension, which is consistent with the center vortex picture. In this theory, gluons can screen quarks, leading to color singlet states with the quantum number of quarks. Casimir scaling is, however, still present at intermediate ranges, i.e. before string breaking occurs. This can be explained by domain formation.

