
Centered number
Encyclopedia
The centered polygonal numbers are a class of series of figurate number
s, each formed by a central dot, surrounded by polygonal layers with a constant number of sides. Each side of a polygonal layer contains one dot more than a side in the previous layer, so starting from the second polygonal layer each layer of a centered k-gonal number contains k more points than the previous layer.
These series consist of the
and so on. The following diagrams show a few examples of centered polygonal numbers and their geometric construction. (Compare these diagrams with the diagrams in Polygonal number
.)
Centered square numbers
Centered hexagonal numbers
As can be seen in the above diagrams, the nth centered k-gonal number can be obtained by placing k copies of the (n−1)th triangular number around a central point; therefore, the nth centered k-gonal number can be mathematically represented by
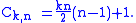
Just as is the case with regular polygonal numbers, the first centered k-gonal number is 1. Thus, for any k, 1 is both k-gonal and centered k-gonal. The next number to be both k-gonal and centered k-gonal can be found using the formula:
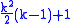
which tells us that 10 is both triangular and centered triangular, 25 is both square and centered square, etc.
Whereas a prime number
p cannot be a polygonal number
(except of course that each p is the second p-agonal number), many centered polygonal numbers are primes.
Figurate number
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes and different dimensions...
s, each formed by a central dot, surrounded by polygonal layers with a constant number of sides. Each side of a polygonal layer contains one dot more than a side in the previous layer, so starting from the second polygonal layer each layer of a centered k-gonal number contains k more points than the previous layer.
These series consist of the
- centered triangular numberCentered triangular numberA centered triangular number is a centered figurate number that represents a triangle with a dot in the center and all other dots surrounding the center in successive triangular layers...
s 1,4,10,19,31,... - centered square numberCentered square numberIn elementary number theory, a centered square number is a centered figurate number that gives the number of dots in a square with a dot in the center and all other dots surrounding the center dot in successive square layers. That is, each centered square number equals the number of dots within a...
s 1,5,13,25,41,... - centered pentagonal numberCentered pentagonal numberA centered pentagonal number is a centered figurate number that represents a pentagon with a dot in the center and all other dots surrounding the center in successive pentagonal layers...
s 1,6,16,31,51,... - centered hexagonal numberCentered hexagonal numberA centered hexagonal number, or hex number, is a centered figurate number that represents a hexagon with a dot in the center and all other dots surrounding the center dot in a hexagonal lattice....
s 1,7,19,37,61,... - centered heptagonal numberCentered heptagonal numberA centered heptagonal number is a centered figurate number that represents a heptagon with a dot in the center and all other dots surrounding the center dot in successive heptagonal layers...
s 1,8,22,43,71,... - centered octagonal numberCentered octagonal numberA centered octagonal number is a centered figurate number that represents an octagon with a dot in the center and all other dots surrounding the center dot in successive octagonal layers...
s 1,9,25,49,81,... - centered nonagonal numberCentered nonagonal numberA centered nonagonal number is a centered figurate number that represents a nonagon with a dot in the center and all other dots surrounding the center dot in successive nonagonal layers...
s 1,10,28,55,91,... ' onMouseout='HidePop("86230")' href="/topics/Perfect_number">perfect numberPerfect numberIn number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
s except 6) - centered decagonal numberCentered decagonal numberA centered decagonal number is a centered figurate number that represents a decagon with a dot in the center and all other dots surrounding the center dot in successive decagonal layers...
s 1,11,31,61,101,...
and so on. The following diagrams show a few examples of centered polygonal numbers and their geometric construction. (Compare these diagrams with the diagrams in Polygonal number
Polygonal number
In mathematics, a polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon. The dots were thought of as alphas . These are one type of 2-dimensional figurate numbers.- Definition and examples :...
.)
Centered square numbers
| 1 | 5 | 13 | 25 | |||
|---|---|---|---|---|---|---|
 |
         |
                         |
                                                 |
Centered hexagonal numbers
| 1 | 7 | 19 | 37 | |||
|---|---|---|---|---|---|---|
 |
       |
                   |
                                     |
As can be seen in the above diagrams, the nth centered k-gonal number can be obtained by placing k copies of the (n−1)th triangular number around a central point; therefore, the nth centered k-gonal number can be mathematically represented by
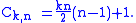
Just as is the case with regular polygonal numbers, the first centered k-gonal number is 1. Thus, for any k, 1 is both k-gonal and centered k-gonal. The next number to be both k-gonal and centered k-gonal can be found using the formula:
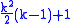
which tells us that 10 is both triangular and centered triangular, 25 is both square and centered square, etc.
Whereas a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p cannot be a polygonal number
Polygonal number
In mathematics, a polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon. The dots were thought of as alphas . These are one type of 2-dimensional figurate numbers.- Definition and examples :...
(except of course that each p is the second p-agonal number), many centered polygonal numbers are primes.

