
Churchill-Bernstein Equation
Encyclopedia
In convective heat transfer
, the Churchill–Bernstein equation is used to estimate the surface averaged Nusselt number
for a cylinder in cross flow at various velocities. The need for the equation arises from the inability to solve the Navier–Stokes equations in the turbulent flow regime, even for a Newtonian fluid
. When the concentration and temperature profiles are independent of one another, the mass-heat transfer analogy can be employed. In the mass-heat transfer analogy, heat transfer dimensionless quantities are replaced with analogous mass transfer
dimensionless quantities.
This equation is named after Stuart W. Churchill and M. Bernstein, who introduced it in 1977. This equation is also called the Churchill–Bernstein correlation.
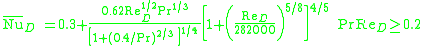
where:
The Churchill–Bernstein equation is valid for a wide range of Reynolds numbers and Prandtl numbers, as long as the product of the two is greater than or equal to 0.2, as defined above. The Churchill–Bernstein equation can be used for any object of cylindrical geometry in which boundary layer
s develop freely, without constraints imposed by other surfaces. Properties of the external free stream fluid are to be evaluated at the film temperature
in order to account for the variation of the fluid properties at different temperatures. One should not expect much more than 20% accuracy from the above equation due to the wide range of flow conditions that the equation encompasses. The Churchill–Bernstein equation is a correlation
and cannot be derived from principles of fluid dynamics
. The equation yields the surface averaged Nusselt number, which is used to determine the average convective heat transfer coefficient. Newton's law of cooling can then be invoked to determine the heat loss or gain from the object, fluid and/or surface temperatures, and the area of the object, depending on what information is known.
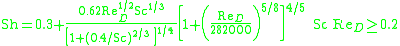
where:
Using the mass-heat transfer analogy, the Nusselt number is replaced by the Sherwood number, and the Prandtl number is replaced by the Schmidt number. The same restrictions described in the heat transfer definition are applied to the mass transfer definition. The Sherwood number can be used to find an overall mass transfer coefficient and applied to Fick's law of diffusion
to find concentration profiles and mass transfer fluxes.
Convective heat transfer
Convective heat transfer, often referred to as convection, is the transfer of heat from one place to another by the movement of fluids. The presence of bulk motion of the fluid enhances the heat transfer between the solid surface and the fluid. Convection is usually the dominant form of heat...
, the Churchill–Bernstein equation is used to estimate the surface averaged Nusselt number
Nusselt number
In heat transfer at a boundary within a fluid, the Nusselt number is the ratio of convective to conductive heat transfer across the boundary. Named after Wilhelm Nusselt, it is a dimensionless number...
for a cylinder in cross flow at various velocities. The need for the equation arises from the inability to solve the Navier–Stokes equations in the turbulent flow regime, even for a Newtonian fluid
Newtonian fluid
A Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:...
. When the concentration and temperature profiles are independent of one another, the mass-heat transfer analogy can be employed. In the mass-heat transfer analogy, heat transfer dimensionless quantities are replaced with analogous mass transfer
Mass transfer
Mass transfer is the net movement of mass from one location, usually meaning a stream, phase, fraction or component, to another. Mass transfer occurs in many processes, such as absorption, evaporation, adsorption, drying, precipitation, membrane filtration, and distillation. Mass transfer is used...
dimensionless quantities.
This equation is named after Stuart W. Churchill and M. Bernstein, who introduced it in 1977. This equation is also called the Churchill–Bernstein correlation.
Heat transfer definition
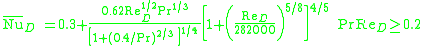
where:
-
 is the surface averaged Nusselt numberNusselt numberIn heat transfer at a boundary within a fluid, the Nusselt number is the ratio of convective to conductive heat transfer across the boundary. Named after Wilhelm Nusselt, it is a dimensionless number...
is the surface averaged Nusselt numberNusselt numberIn heat transfer at a boundary within a fluid, the Nusselt number is the ratio of convective to conductive heat transfer across the boundary. Named after Wilhelm Nusselt, it is a dimensionless number...
with characteristic length of diameter; -
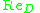 is the Reynolds number with the cylinder diameter as its characteristic length;
is the Reynolds number with the cylinder diameter as its characteristic length; -
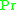 is the Prandtl number.
is the Prandtl number.
The Churchill–Bernstein equation is valid for a wide range of Reynolds numbers and Prandtl numbers, as long as the product of the two is greater than or equal to 0.2, as defined above. The Churchill–Bernstein equation can be used for any object of cylindrical geometry in which boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
s develop freely, without constraints imposed by other surfaces. Properties of the external free stream fluid are to be evaluated at the film temperature
Film Temperature
In heat transfer and fluid dynamics, the film temperature is an approximation to the temperature of a fluid inside a convection boundary layer...
in order to account for the variation of the fluid properties at different temperatures. One should not expect much more than 20% accuracy from the above equation due to the wide range of flow conditions that the equation encompasses. The Churchill–Bernstein equation is a correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
and cannot be derived from principles of fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
. The equation yields the surface averaged Nusselt number, which is used to determine the average convective heat transfer coefficient. Newton's law of cooling can then be invoked to determine the heat loss or gain from the object, fluid and/or surface temperatures, and the area of the object, depending on what information is known.
Mass transfer definition
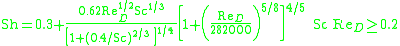
where:
-
 is the Sherwood number
is the Sherwood number -
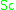 is the Schmidt numberSchmidt numberSchmidt number is a dimensionless number defined as the ratio of momentum diffusivity and mass diffusivity, and is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes...
is the Schmidt numberSchmidt numberSchmidt number is a dimensionless number defined as the ratio of momentum diffusivity and mass diffusivity, and is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes...
Using the mass-heat transfer analogy, the Nusselt number is replaced by the Sherwood number, and the Prandtl number is replaced by the Schmidt number. The same restrictions described in the heat transfer definition are applied to the mass transfer definition. The Sherwood number can be used to find an overall mass transfer coefficient and applied to Fick's law of diffusion
Fick's law of diffusion
Fick's laws of diffusion describe diffusion and can be used to solve for the diffusion coefficient, D. They were derived by Adolf Fick in the year 1855.- Fick's first law :...
to find concentration profiles and mass transfer fluxes.

