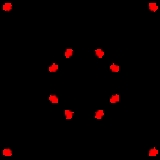
Chvátal graph
Encyclopedia
In the mathematical
field of graph theory
, the Chvátal graph is an undirected graph with 12 vertices and 24 edges, discovered by .
It is triangle-free
: its girth (the length of its shortest cycle) is four. It is 4-regular
: each vertex has exactly four neighbors. And its chromatic number is 4: it can be colored using four colors, but not using only three. It is, as Chvátal observes, the smallest possible 4-chromatic 4-regular triangle-free graph; the only smaller 4-chromatic triangle-free graph is the Grötzsch graph
, which has 11 vertices but has maximum degree 5 and is not regular.
By Brooks’ theorem
, every k-regular graph (except for odd cycles and cliques) has chromatic number at most k. It was also known since that, for every k and l there exist k-chromatic graphs with girth l. In connection with these two results and several examples including the Chvátal graph,
conjectured that for every k and l there exist k-chromatic k-regular graphs with girth l. The Chvátal graph solves the case k = l = 4 of this conjecture. Grünbaum's conjecture was disproven for sufficiently large k by Johannsen (see ), who showed that the chromatic number of a triangle-free graph is O(Δ/log Δ) where Δ is the maximum vertex degree and the O introduces big O notation
. However, despite this disproof, it remains of interest to find examples such as the Chvátal graph of high-girth k-chromatic k-regular graphs for small values of k.
An alternative conjecture of states that high-degree triangle-free graphs must have significantly smaller chromatic number than their degree, and more generally that a graph with maximum degree Δ and maximum clique size ω must have chromatic number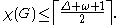
The case ω = 2 of this conjecture follows, for sufficiently large Δ, from Johanssen's result. The Chvátal graph shows that the rounding up in Reed's conjecture is necessary, because for the Chvátal graph, (Δ + ω + 1)/2 = 7/2, a number that is less than the chromatic number but that becomes equal to the chromatic number when rounded up.
The Chvátal graph is Hamiltonian, and plays a key role in a proof by that it is NP-complete
to determine whether a triangle-free Hamiltonian graph is 3-colorable.
The characteristic polynomial
of the Chvátal graph is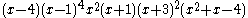
. The Tutte polynomial
of the Chvátal graph has been computed by .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Chvátal graph is an undirected graph with 12 vertices and 24 edges, discovered by .
It is triangle-free
Triangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
: its girth (the length of its shortest cycle) is four. It is 4-regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
: each vertex has exactly four neighbors. And its chromatic number is 4: it can be colored using four colors, but not using only three. It is, as Chvátal observes, the smallest possible 4-chromatic 4-regular triangle-free graph; the only smaller 4-chromatic triangle-free graph is the Grötzsch graph
Grötzsch graph
In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, and chromatic number 4. It is named after German mathematician Herbert Grötzsch, and its existence demonstrates that the assumption of planarity is necessary in Grötzsch's theorem ...
, which has 11 vertices but has maximum degree 5 and is not regular.
By Brooks’ theorem
Brooks’ theorem
In graph theory, Brooks' theorem states a relationship between the maximum degree of a graph and its chromatic number. According to the theorem, in a graph in which every vertex has at most Δ neighbors, the vertices may be colored with only Δ colors, except for two cases, complete graphs and cycle...
, every k-regular graph (except for odd cycles and cliques) has chromatic number at most k. It was also known since that, for every k and l there exist k-chromatic graphs with girth l. In connection with these two results and several examples including the Chvátal graph,
conjectured that for every k and l there exist k-chromatic k-regular graphs with girth l. The Chvátal graph solves the case k = l = 4 of this conjecture. Grünbaum's conjecture was disproven for sufficiently large k by Johannsen (see ), who showed that the chromatic number of a triangle-free graph is O(Δ/log Δ) where Δ is the maximum vertex degree and the O introduces big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
. However, despite this disproof, it remains of interest to find examples such as the Chvátal graph of high-girth k-chromatic k-regular graphs for small values of k.
An alternative conjecture of states that high-degree triangle-free graphs must have significantly smaller chromatic number than their degree, and more generally that a graph with maximum degree Δ and maximum clique size ω must have chromatic number
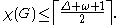
The case ω = 2 of this conjecture follows, for sufficiently large Δ, from Johanssen's result. The Chvátal graph shows that the rounding up in Reed's conjecture is necessary, because for the Chvátal graph, (Δ + ω + 1)/2 = 7/2, a number that is less than the chromatic number but that becomes equal to the chromatic number when rounded up.
The Chvátal graph is Hamiltonian, and plays a key role in a proof by that it is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
to determine whether a triangle-free Hamiltonian graph is 3-colorable.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Chvátal graph is
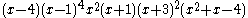. The Tutte polynomialTutte polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
of the Chvátal graph has been computed by .