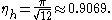In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, circle packing is the study of the arrangement of circles (of equal or varying sizes) on a given surface such that no overlapping occurs and so that all circles touch another. The associated "packing density", η of an arrangement is the proportion of the surface covered by the circles. Generalisations can be made to higher dimensions – this is called sphere packing

Sphere packing

In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...

, which usually deals only with identical spheres.

The branch of mathematics generally known as "circle packing", however, is not overly concerned with dense packing of equal-sized circles (the densest packing is known) but with the geometry and combinatorics of packings of arbitrarily-sized circles: these give rise to discrete analogs of conformal mapping, Riemann surfaces and the like.

While the circle has a relatively low maximum packing density, it does not have the lowest possible. The "worst" shape to pack onto a plane is not known, but the smoothed octagon

Smoothed octagon

The smoothed octagon is a geometrical construction conjectured to have the lowest maximum packing density of the plane of all centrally symmetric convex shapes...

 has a packing density of about 0.902414, which is the lowest maximum packing density known of any centrally-symmetric convex shape.
Packing densities of concave shapes such as star polygons can be arbitrarily small.

Packings in the plane

In two dimensional Euclidean space, Joseph Louis Lagrange

Joseph Louis Lagrange

Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...

 proved in 1773 that the lattice arrangement of circles with the highest density is the hexagonal packing arrangement, in which the centres of the circles are arranged in a hexagonal lattice (staggered rows, like a honeycomb

Honeycomb

A honeycomb is a mass of hexagonal waxcells built by honey bees in their nests to contain their larvae and stores of honey and pollen.Beekeepers may remove the entire honeycomb to harvest honey...

), and each circle is surrounded by 6 other circles. The density of this arrangement is

Axel Thue

Axel Thue

Axel Thue was a Norwegian mathematician, known for highly original work in diophantine approximation, and combinatorics....

 provided the first proof that this was optimal in 1890, showing that the hexagonal lattice is the densest of all possible circle packings, both regular and irregular. However, his proof was considered by some to be incomplete. The first rigorous proof is attributed to László Fejes Tóth

László Fejes Tóth

László Fejes Tóth was a Hungarian mathematician who specialised in geometry. He proved that a honeycomb pattern is the most efficient way to pack centrally symmetric convex sets on the Euclidean plane . He also investigated packings on the sphere...

 in 1940.

At the other extreme, very low density arrangements of rigidly packed circles have been identified.

Packings on the sphere

A related problem is to determine the lowest-energy arrangement of identically interacting points that are constrained to lie within a given surface. The Thomson problem

Thomson problem

The Thomson problem is to determine the minimum energy configuration of N electrons on the surface of a sphere that repel each other with a force given by Coulomb's law. The physicist J. J...

 deals with the lowest energy distribution of identical electric charges on the surface of a sphere. The Tammes problem

Tammes problem

In geometry, Tammes problem is a problem in packing a given number of circles on the surface of a sphere such that the minimum distance between circles is maximized. It is named after a Dutch botanist who posed the problem in 1930 while studying the distribution of pores on pollen grains...

 is a generalisation of this, dealing with maximising the minimum distance between circles on sphere. This is analogous to distributing non-point charges on a sphere.

Packings in bounded areas

Packing circles in simple bounded shapes is a common type of problem in recreational mathematics

Recreational mathematics

Recreational mathematics is an umbrella term, referring to mathematical puzzles and mathematical games.Not all problems in this field require a knowledge of advanced mathematics, and thus, recreational mathematics often attracts the curiosity of non-mathematicians, and inspires their further study...

. The influence of the container walls is important, and hexagonal packing is generally not optimal for small numbers of circles.

Unequal circles

There are also a range of problems which permit the sizes of the circles to be non-uniform. One such extension is to find the maximum possible density of a system with two specific sizes of circle (a binary system). Only nine particular radius ratios permit compact packing, which is when every pair of circles in contact is in mutual contact with two other circles (when line segments are drawn from contacting circle-center to circle-center, they triangulate the surface).

See also

• Circle packing in a square
  Circle packing in a square
  Circle packing in a square is a packing problem in recreational mathematics, where the aim is to pack n unit circles into the smallest possible square; or, equivalently, to arrange n points in a unit square for the greatest minimal separation, dn, between points...
  
  
• Apollonian gasket
  Apollonian gasket
  In mathematics, an Apollonian gasket or Apollonian net is a fractal generated from triples of circles, where each circle is tangent to the other two. It is named after Greek mathematician Apollonius of Perga.-Construction:...
  
  
• Kepler conjecture
  Kepler conjecture
  The Kepler conjecture, named after the 17th-century German astronomer Johannes Kepler, is a mathematical conjecture about sphere packing in three-dimensional Euclidean space. It says that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic...
  
  
• Malfatti circles
  Malfatti circles
  In geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the triangle...
  
  
• Packing problem
  Packing problem
  Packing problems are a class of optimization problems in mathematics which involve attempting to pack objects together , as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues...