
Malfatti circles
Encyclopedia
In geometry
, the Malfatti circles are three circle
s inside a given triangle
such that each circle is tangent
to the other two and to two sides of the triangle. They are named after Gian Francesco Malfatti
, who made early studies of the problem of constructing these circles in the mistaken belief that they would have the largest possible total area of any three disjoint circles within the triangle. Malfatti's problem has been used to refer both to the problem of constructing the Malfatti circles and to the problem of finding three area-maximizing circles within a triangle.
posed the problem of cutting three cylindrical column
s out of a rectangular wedge
of marble, maximizing the total volume of the columns. He assumed, as did many others after him, that the solution to this problem was given by three tangent circles within the triangular cross-section of the wedge. That is, more abstractly, he conjectured that the three Malfatti circles have the maximum total area of any three disjoint circles within a given triangle.
Malfatti published in Italian and his work may not have been read by many in the original. It was popularised for a wider readership in French by Joseph Diaz Gergonne in the first volume of his ``Annales" (1810/11), with further discussion in the second and tenth. However, this advertisement most likely acted as a filter, as Gergonne only stated the circle-tangency problem, not the area-maximizing one.
The conjecture is wrong; , who went back to the original Italian text, observed that for some triangles a larger area can be achieved by a greedy algorithm
that inscribes a single circle of maximal radius within the triangle, inscribes a second circle within the largest of the three remaining corners of the triangle, and inscribes a third circle within the largest of the five remaining pieces. The difference in area for an equilateral triangle is small, just over 1%, but as Howard Eves
pointed out in 1946, for an isosceles triangle with a very sharp apex, the optimal circles (stacked one atop each other above the base of the triangle) have nearly twice the area of the Malfatti circles.
showed that, for every triangle, the Lob–Richmond procedure produces three circles with larger area than the Malfatti circles, so the Malfatti circles are never optimal. classified all of the different ways that a set of maximal circles can be packed within a triangle; using their classification, they proved that the greedy algorithm always finds three area-maximizing circles, and they provided a formula for determining which packing is optimal for a given triangle. In his 1997 Ph.D. thesis, Melissen conjectured more generally that, for any integer , the greedy algorithm finds the area-maximizing set of circles within a given triangle; the conjecture is known to be true for .
of Sienna
, Italy
.
Since the work of Malfatti, there has been a significant amount of work on methods for constructing Malfatti's three tangent circles; Richard K. Guy
writes that the literature on the problem is "extensive, widely scattered, and not always aware of itself". Notably, in 1826 Jakob Steiner
presented a simple geometric construction based on bitangent
s; other authors have since claimed that Steiner's presentation lacked a proof, which was later supplied by Andrew Hart
(1856), but Guy points to the proof scattered within two of Steiner's own papers from that time. Lob and Richmond cite solutions by C. L. Lehmus
(1819), Eugène Charles Catalan
(1845), J. Derousseau (1895), A. Pampuch (1904), and J. L. Coolidge (1916), all based on algebraic formulations of the problem. The algebraic solutions do not distinguish between internal and external tangencies among the circles and the given triangle; if the problem is generalized to allow tangencies of either kind, then a given triangle will have 32 different solutions and conversely a triple of mutually tangent circles will be a solution for eight different triangles. Bottema and Guy cite additional work on the problem and its generalizations by C. Adams (1846), Adolphe Quidde (1850), K. H. Schellbach (1853), Arthur Cayley
(1854, 1857, 1875), Alfred Clebsch
(1857), P. Simons (1874), J. Casey
(1888), Rouché and Comberousse (1900), H. F. Baker
(1925), L. J. Rogers
(1928), Angelo Procissi (1932), Jun Naito (1975), and D. G. Rogers (2005).
Gatto and Mazotti recount an episode in 19th-century Neapolitan
mathematics related to the Malfatti circles. In 1839, Vincenzo Flauti, a synthetic geometer
, posed a challenge involving the solution of three geometry problems, one of which was the construction of Malfatti's circles; his intention in doing so was to show the superiority of synthetic to analytic techniques. Despite a solution being given by Fortunato Padula, a student in a rival school of analytic geometry
, Flauti awarded the prize to his own student, Nicola Trudi, whose solutions Flauti had known of when he posed his challenge. More recently, the problem of constructing the Malfatti circles has been used as a test problem for computer algebra system
s.
, in 1826 Jakob Steiner
provided the following simple synthetic
construction.
A circle that is tangent to two sides of a triangle, as the Malfatti circles are, must be centered on one of the angle bisectors of the triangle (green in the figure). These bisectors partition the triangle into three smaller triangles, and Steiner's construction of the Malfatti circles begins by drawing a different triple of circles (shown dashed in the figure) inscribed within each of these three smaller triangles. Each pair of two of these three inscribed circles has two bitangent
s, lines that touch both of the dashed circles and pass between them: one bitangent is the angle bisector, and the second bitangent is shown as the red dashed line in the figure. Label the three sides of the given triangle as , , and , and label the three bitangents that are not angle bisectors as , , and , where is the bitangent to the two circles that do not touch side , is the bitangent to the two circles that do not touch side , and is the bitangent to the two circles that do not touch side . Then the three Malfatti circles are the inscribed circles to the three tangential quadrilateral
s , , and . The three bitangents , , and cross the triangle sides at the point of tangency with the third inscribed circle, and may also be found as the reflections of the angle bisectors across the lines connecting pairs of centers of these incircles.
of each of the three Malfatti circles may be determined as a formula involving the three side lengths , , and of the triangle, the inradius , the semiperimeter
, and the three distances , , and from the incenter of the triangle to the vertices opposite sides , , and respectively. The formulae for the three radii are: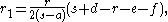
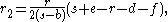 and
and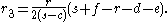
According to , these formulae were discovered by Malfatti and published posthumously by him in 1811.
Related formulae may be used to find examples of triangles whose side lengths, inradii, and Malfatti radii are all rational number
s or all integers. For instance, the triangle with side lengths 28392, 21000, and 25872 has inradius 6930 and Malfatti radii 3969, 4900, and 4356. As another example, the triangle with side lengths 152460, 165000, and 190740 has inradius 47520 and Malfatti radii 27225, 30976, and 32400.
known as the first Ajima–Malfatti point after the contributions of Ajima and Malfatti to the circle problem. The second Ajima–Malfatti point is the meeting point of three lines connecting the tangencies of the Malfatti circles with the centers of the excircles of the triangle. Other triangle centers also associated with the Malfatti circles include the Yff–Malfatti point, formed in the same way as the first Malfatti point from three mutually tangent circles that are all tangent to the lines through the sides of the given triangle, but that lie partially outside the triangle, and the radical center of the three Malfatti circles.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Malfatti circles are three circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s inside a given triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
such that each circle is tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the other two and to two sides of the triangle. They are named after Gian Francesco Malfatti
Gian Francesco Malfatti
Giovanni Francesco Giuseppe, also known as Gian Francesco or Gianfrancesco was an Italian mathematician. He was born in Ala, Trentino, Italy and died in Ferrara....
, who made early studies of the problem of constructing these circles in the mistaken belief that they would have the largest possible total area of any three disjoint circles within the triangle. Malfatti's problem has been used to refer both to the problem of constructing the Malfatti circles and to the problem of finding three area-maximizing circles within a triangle.
Malfatti's problem
In 1803 Gian Francesco MalfattiGian Francesco Malfatti
Giovanni Francesco Giuseppe, also known as Gian Francesco or Gianfrancesco was an Italian mathematician. He was born in Ala, Trentino, Italy and died in Ferrara....
posed the problem of cutting three cylindrical column
Column
A column or pillar in architecture and structural engineering is a vertical structural element that transmits, through compression, the weight of the structure above to other structural elements below. For the purpose of wind or earthquake engineering, columns may be designed to resist lateral forces...
s out of a rectangular wedge
Wedge (geometry)
In solid geometry, a wedge is a polyhedron defined by two triangles and three trapezoid faces. A wedge has five faces, nine edges, and six vertices.A wedge is a subclass of the prismatoids with the base and opposite ridge in two parallel planes....
of marble, maximizing the total volume of the columns. He assumed, as did many others after him, that the solution to this problem was given by three tangent circles within the triangular cross-section of the wedge. That is, more abstractly, he conjectured that the three Malfatti circles have the maximum total area of any three disjoint circles within a given triangle.
Malfatti published in Italian and his work may not have been read by many in the original. It was popularised for a wider readership in French by Joseph Diaz Gergonne in the first volume of his ``Annales" (1810/11), with further discussion in the second and tenth. However, this advertisement most likely acted as a filter, as Gergonne only stated the circle-tangency problem, not the area-maximizing one.
The conjecture is wrong; , who went back to the original Italian text, observed that for some triangles a larger area can be achieved by a greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
that inscribes a single circle of maximal radius within the triangle, inscribes a second circle within the largest of the three remaining corners of the triangle, and inscribes a third circle within the largest of the five remaining pieces. The difference in area for an equilateral triangle is small, just over 1%, but as Howard Eves
Howard Eves
Howard Whitley Eves was an American mathematician, known for his work in geometry and the history of mathematics....
pointed out in 1946, for an isosceles triangle with a very sharp apex, the optimal circles (stacked one atop each other above the base of the triangle) have nearly twice the area of the Malfatti circles.
showed that, for every triangle, the Lob–Richmond procedure produces three circles with larger area than the Malfatti circles, so the Malfatti circles are never optimal. classified all of the different ways that a set of maximal circles can be packed within a triangle; using their classification, they proved that the greedy algorithm always finds three area-maximizing circles, and they provided a formula for determining which packing is optimal for a given triangle. In his 1997 Ph.D. thesis, Melissen conjectured more generally that, for any integer , the greedy algorithm finds the area-maximizing set of circles within a given triangle; the conjecture is known to be true for .
History
The problem of constructing three circles tangent to each other within a triangle was posed by the 18th-century Japanese mathematician Ajima Naonobu prior to the work of Malfatti, and included in an unpublished collection of Ajima's works made a year after Ajima's death by his student Kusaka Makoto. Even earlier, the same problem was considered in a 1384 manuscript by Gilio di Cecco da Montepulciano, now in the Municipal LibraryBiblioteca Comunale (Siena)
The Biblioteca Comunale is a municipal library in Siena, Italy.The library was opened to the public use in 1759 by Sallustio Bandini. The first librarian of the library was Giuseppe Ciaccheri . He was interested in everything related to the arts in Siena. In 1774 the library contained more than...
of Sienna
Sienna
Sienna is a form of limonite clay most famous in the production of oil paint pigments. Its yellow-brown colour comes from ferric oxides contained within...
, Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
.
Since the work of Malfatti, there has been a significant amount of work on methods for constructing Malfatti's three tangent circles; Richard K. Guy
Richard K. Guy
Richard Kenneth Guy is a British mathematician, Professor Emeritus in the Department of Mathematics at the University of Calgary....
writes that the literature on the problem is "extensive, widely scattered, and not always aware of itself". Notably, in 1826 Jakob Steiner
Jakob Steiner
Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...
presented a simple geometric construction based on bitangent
Bitangent
In mathematics, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction to C at these points...
s; other authors have since claimed that Steiner's presentation lacked a proof, which was later supplied by Andrew Hart
Andrew Searle Hart
Sir Andrew Searle Hart , mathematician and vice-provost of Trinity College, Dublin.Hart, youngest son of the Rev. George Vaughan Hart of Glenalla, County Donegal, by Maria Murray, daughter of the Very Rev. John Hume, dean of Derry, was born at Limerick on...
(1856), but Guy points to the proof scattered within two of Steiner's own papers from that time. Lob and Richmond cite solutions by C. L. Lehmus
C. L. Lehmus
Daniel Christian Ludolph Lehmus was a German mathematician, who is today best remembered for the Steiner–Lehmus theorem, that was named after him....
(1819), Eugène Charles Catalan
Eugène Charles Catalan
Eugène Charles Catalan was a French and Belgian mathematician.- Biography :Catalan was born in Bruges , the only child of a French jeweller by the name of Joseph Catalan, in 1814. In 1825, he traveled to Paris and learned mathematics at École Polytechnique, where he met Joseph Liouville...
(1845), J. Derousseau (1895), A. Pampuch (1904), and J. L. Coolidge (1916), all based on algebraic formulations of the problem. The algebraic solutions do not distinguish between internal and external tangencies among the circles and the given triangle; if the problem is generalized to allow tangencies of either kind, then a given triangle will have 32 different solutions and conversely a triple of mutually tangent circles will be a solution for eight different triangles. Bottema and Guy cite additional work on the problem and its generalizations by C. Adams (1846), Adolphe Quidde (1850), K. H. Schellbach (1853), Arthur Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
(1854, 1857, 1875), Alfred Clebsch
Alfred Clebsch
Rudolf Friedrich Alfred Clebsch was a German mathematician who made important contributions to algebraic geometry and invariant theory. He attended the University of Königsberg and was habilitated at Berlin. He subsequently taught in Berlin and Karlsruhe...
(1857), P. Simons (1874), J. Casey
John Casey (mathematician)
John Casey was a respected Irish geometer. He is most famous for Casey's theorem on a circle that is tangent to four other circles, an extension of the problem of Apollonius. However, he contributed several novel proofs and perspectives on Euclidean geometry...
(1888), Rouché and Comberousse (1900), H. F. Baker
H. F. Baker
Henry Frederick Baker was a British mathematician, working mainly in algebraic geometry, but also remembered for contributions to partial differential equations , and Lie groups....
(1925), L. J. Rogers
Leonard James Rogers
Leonard James Rogers FRS was a British mathematician who was the first to discover the Rogers-Ramanujan identity and Hölder's inequality, and who introduced Rogers polynomials...
(1928), Angelo Procissi (1932), Jun Naito (1975), and D. G. Rogers (2005).
Gatto and Mazotti recount an episode in 19th-century Neapolitan
Kingdom of the Two Sicilies
The Kingdom of the Two Sicilies, commonly known as the Two Sicilies even before formally coming into being, was the largest and wealthiest of the Italian states before Italian unification...
mathematics related to the Malfatti circles. In 1839, Vincenzo Flauti, a synthetic geometer
Synthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
, posed a challenge involving the solution of three geometry problems, one of which was the construction of Malfatti's circles; his intention in doing so was to show the superiority of synthetic to analytic techniques. Despite a solution being given by Fortunato Padula, a student in a rival school of analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, Flauti awarded the prize to his own student, Nicola Trudi, whose solutions Flauti had known of when he posed his challenge. More recently, the problem of constructing the Malfatti circles has been used as a test problem for computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s.
Steiner's construction
Although much of the early work on the Malfatti circles used analytic geometryAnalytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, in 1826 Jakob Steiner
Jakob Steiner
Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...
provided the following simple synthetic
Synthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
construction.
A circle that is tangent to two sides of a triangle, as the Malfatti circles are, must be centered on one of the angle bisectors of the triangle (green in the figure). These bisectors partition the triangle into three smaller triangles, and Steiner's construction of the Malfatti circles begins by drawing a different triple of circles (shown dashed in the figure) inscribed within each of these three smaller triangles. Each pair of two of these three inscribed circles has two bitangent
Bitangent
In mathematics, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction to C at these points...
s, lines that touch both of the dashed circles and pass between them: one bitangent is the angle bisector, and the second bitangent is shown as the red dashed line in the figure. Label the three sides of the given triangle as , , and , and label the three bitangents that are not angle bisectors as , , and , where is the bitangent to the two circles that do not touch side , is the bitangent to the two circles that do not touch side , and is the bitangent to the two circles that do not touch side . Then the three Malfatti circles are the inscribed circles to the three tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
s , , and . The three bitangents , , and cross the triangle sides at the point of tangency with the third inscribed circle, and may also be found as the reflections of the angle bisectors across the lines connecting pairs of centers of these incircles.
Radius formula
The radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of each of the three Malfatti circles may be determined as a formula involving the three side lengths , , and of the triangle, the inradius , the semiperimeter
Semiperimeter
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name...
, and the three distances , , and from the incenter of the triangle to the vertices opposite sides , , and respectively. The formulae for the three radii are:
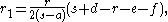
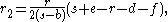 and
and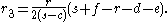
According to , these formulae were discovered by Malfatti and published posthumously by him in 1811.
Related formulae may be used to find examples of triangles whose side lengths, inradii, and Malfatti radii are all rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s or all integers. For instance, the triangle with side lengths 28392, 21000, and 25872 has inradius 6930 and Malfatti radii 3969, 4900, and 4356. As another example, the triangle with side lengths 152460, 165000, and 190740 has inradius 47520 and Malfatti radii 27225, 30976, and 32400.
Ajima–Malfatti points
Given a triangle ABC and its three Malfatti circles, let D, E, and F be the points where two of the circles touch each other, opposite vertices A, B, and C respectively. Then the three lines AD, BE, and CF meet in a single triangle centerTriangle center
In geometry a triangle center is a point in the plane that is in some sense a center of a triangle akin to the centers of squares and circles. For example the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions. Each of...
known as the first Ajima–Malfatti point after the contributions of Ajima and Malfatti to the circle problem. The second Ajima–Malfatti point is the meeting point of three lines connecting the tangencies of the Malfatti circles with the centers of the excircles of the triangle. Other triangle centers also associated with the Malfatti circles include the Yff–Malfatti point, formed in the same way as the first Malfatti point from three mutually tangent circles that are all tangent to the lines through the sides of the given triangle, but that lie partially outside the triangle, and the radical center of the three Malfatti circles.
See also
- Circle packing in an equilateral triangleCircle packing in an equilateral triangleCircle packing in an equilateral triangle is a packing problem in discrete mathematics where the objective is to pack n unit circles into the smallest possible equilateral triangle...
- Circle packing in an isosceles right triangleCircle packing in an isosceles right triangleCircle packing in a right isosceles triangle is a packing problem where the objective is to pack n unit circles into the smallest possible isosceles right triangle.Minimum solutions are shown in the table below...
- Six circles theoremSix circles theoremIn geometry, the six circles theorem relates to a chain of six circles together with a triangle, such that each circle is tangent to two sides of the triangle and also to the preceding circle in the chain...
External links
- Malfatti's Problem at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...

