Thomson problem
Encyclopedia
The Thomson problem is to determine the minimum energy configuration of N electron
s on the surface of a sphere that repel each other with a force given by Coulomb's law
. The physicist J. J. Thomson
posed the problem in 1904 after creating his so-called plum pudding model
of the atom
.
Related problems include the study of the geometry of the minimum energy configuration and the study of the large N behavior of the minimum energy.
be a collection of 
distinct points on the unit sphere
centered at the origin.
The energy of this configuration of points is defined to be
.
Thomson's problem is to minimize this energy over all possible collections of
distinct points
on the unit sphere.
In the case of two points, the optimal configuration consists of antipodal points.
For N=3, three equidistant points on a great circle
realize the minimum energy configuration.
. The vertices of a regular tetrahedron
minimize the energy in the case of 4 points. Yudin showed that the vertices of the regular octahedron
solve the problem in the case of 6 vertices. N.N. Andreev provides a method to prove that the vertex set of the regular icosahedron
provides a solution in the case of 12 vertices.
In 2010, Richard Schwartz announced a mathematically rigorous computer-aided solution for 5 points.
To be mathematically precise, let f be a decreasing real-valued function, and define the energy functional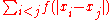
Traditionally, one considers
. Notable cases include α=∞, the Tammes problem
(packing); α=1, the Thomson problem; α=0, Whyte's problem (to maximize the product of distances).
One may also consider configurations of N points on a sphere of higher dimension.
, Thomson's problem has since found
a role in the study of other physical models.
These include multi-electron bubbles and the surface ordering of liquid metal drops confined in Pauli traps.
The generalized Thomson problem arises, for example, in determining the arrangements of the protein subunits which comprise the shells of spherical virus
es. The "particles" in this application are clusters of protein subunits arranged on a shell. Other realizations include regular arrangements of colloid
particles in colloidosomes, proposed for encapsulation of active ingredients such as drugs, nutrients or living cells, fullerene
patterns of carbon atoms, and VSEPR Theory
. An example with long-range logarithmic interactions is provided by the Abrikosov vortices which would form at low temperatures in a superconducting
metal shell with a large monopole at the center.
is the number of points (charges) in a configuration. 
is the energy. The symmetry type is given in Schönflies notation (see Point groups in three dimensions
).
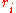are the positions of the charges. Most symmetry types require the sum (and thus the electric dipole moment
) to be zero.
It is customary to also consider the polyhedron formed by the convex hull
of the points. Thus
is the number of vertices where the given number of edges meet. 
is the total number of edges 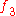and 
and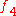 
are the number of triangle and quadrilateral faces. 
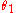is the smallest angle between any two points.
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s on the surface of a sphere that repel each other with a force given by Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
. The physicist J. J. Thomson
J. J. Thomson
Sir Joseph John "J. J." Thomson, OM, FRS was a British physicist and Nobel laureate. He is credited for the discovery of the electron and of isotopes, and the invention of the mass spectrometer...
posed the problem in 1904 after creating his so-called plum pudding model
Plum pudding model
The plum pudding model of the atom by J. J. Thomson, who discovered the electron in 1897, was proposed in 1904 before the discovery of the atomic nucleus. In this model, the atom is composed of electrons The plum pudding model of the atom by J. J. Thomson, who discovered the electron in 1897, was...
of the atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
.
Related problems include the study of the geometry of the minimum energy configuration and the study of the large N behavior of the minimum energy.
Mathematical statement
Let be a collection of distinct points on the unit sphereUnit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
centered at the origin.
The energy of this configuration of points is defined to be
.Thomson's problem is to minimize this energy over all possible collections of
distinct pointson the unit sphere.
Known solutions
Minimal energy configurations have been rigorously identified in only a handful of cases.In the case of two points, the optimal configuration consists of antipodal points.
For N=3, three equidistant points on a great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
realize the minimum energy configuration.
. The vertices of a regular tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
minimize the energy in the case of 4 points. Yudin showed that the vertices of the regular octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
solve the problem in the case of 6 vertices. N.N. Andreev provides a method to prove that the vertex set of the regular icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
provides a solution in the case of 12 vertices.
In 2010, Richard Schwartz announced a mathematically rigorous computer-aided solution for 5 points.
Generalizations
One can also ask for ground states of particles interacting with arbitrary potentials.To be mathematically precise, let f be a decreasing real-valued function, and define the energy functional
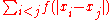
Traditionally, one considers
. Notable cases include α=∞, the Tammes problemTammes problem
In geometry, Tammes problem is a problem in packing a given number of circles on the surface of a sphere such that the minimum distance between circles is maximized. It is named after a Dutch botanist who posed the problem in 1930 while studying the distribution of pores on pollen grains...
(packing); α=1, the Thomson problem; α=0, Whyte's problem (to maximize the product of distances).
One may also consider configurations of N points on a sphere of higher dimension.
Relations to other scientific problems
Though experimental evidence led to the abandonment of Thomson's plum pudding modelPlum pudding model
The plum pudding model of the atom by J. J. Thomson, who discovered the electron in 1897, was proposed in 1904 before the discovery of the atomic nucleus. In this model, the atom is composed of electrons The plum pudding model of the atom by J. J. Thomson, who discovered the electron in 1897, was...
, Thomson's problem has since found
a role in the study of other physical models.
These include multi-electron bubbles and the surface ordering of liquid metal drops confined in Pauli traps.
The generalized Thomson problem arises, for example, in determining the arrangements of the protein subunits which comprise the shells of spherical virus
Virus
A virus is a small infectious agent that can replicate only inside the living cells of organisms. Viruses infect all types of organisms, from animals and plants to bacteria and archaea...
es. The "particles" in this application are clusters of protein subunits arranged on a shell. Other realizations include regular arrangements of colloid
Colloid
A colloid is a substance microscopically dispersed evenly throughout another substance.A colloidal system consists of two separate phases: a dispersed phase and a continuous phase . A colloidal system may be solid, liquid, or gaseous.Many familiar substances are colloids, as shown in the chart below...
particles in colloidosomes, proposed for encapsulation of active ingredients such as drugs, nutrients or living cells, fullerene
Fullerene
A fullerene is any molecule composed entirely of carbon, in the form of a hollow sphere, ellipsoid, or tube. Spherical fullerenes are also called buckyballs, and they resemble the balls used in association football. Cylindrical ones are called carbon nanotubes or buckytubes...
patterns of carbon atoms, and VSEPR Theory
VSEPR theory
Valence shell electron pair repulsion theory is a model in chemistry used to predict the shape of individual molecules based upon the extent of electron-pair electrostatic repulsion. It is also named Gillespie–Nyholm theory after its two main developers...
. An example with long-range logarithmic interactions is provided by the Abrikosov vortices which would form at low temperatures in a superconducting
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
metal shell with a large monopole at the center.
Configurations of smallest known energy
In the following table is the number of points (charges) in a configuration. is the energy. The symmetry type is given in Schönflies notation (see Point groups in three dimensionsPoint groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
).
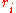are the positions of the charges. Most symmetry types require the sum (and thus the electric dipole momentElectric dipole moment
In physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter...
) to be zero.
It is customary to also consider the polyhedron formed by the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the points. Thus
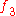is the number of vertices where the given number of edges meet. is the total number of edges and and 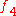are the number of triangle and quadrilateral faces. 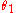is the smallest angle between any two points.| N |  |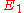
Symmetry Point groups in three dimensions In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group... |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
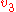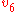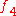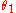Equivalent Polyhedron | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.500000000 |  |
0 | - | - | - | - | - | - | - | - | - | 180.000° | |
| 3 | 1.732050808 |  |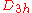
0 | - | - | - | - | - | - | - | - | - | 120.000° | |
| 4 | 3.674234614 |  |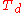
0 | 4 | 0 | 0 | 0 | 0 | 0 | 6 | 4 | 0 | 109.471° | tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
| 5 | 6.474691495 |  |
0 | 2 | 3 | 0 | 0 | 0 | 0 | 9 | 6 | 0 | 90.000° | triangular dipyramid Triangular dipyramid In geometry, the triangular bipyramid is the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.... |
| 6 | 9.985281374 |  |
0 | 0 | 6 | 0 | 0 | 0 | 0 | 12 | 8 | 0 | 90.000° | octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
| 7 | 14.452997414 |  |
0 | 0 | 5 | 2 | 0 | 0 | 0 | 15 | 10 | 0 | 72.000° | pentagonal dipyramid Pentagonal dipyramid In geometry, the pentagonal bipyramid is third of the infinite set of face-transitive bipyramids.Each bipyramid is the dual of a uniform prism.If the faces are equilateral triangles, it is a deltahedron and a Johnson solid... |
| 8 | 19.675287861 |  |
0 | 0 | 8 | 0 | 0 | 0 | 0 | 16 | 8 | 2 | 71.694° | square antiprism Square antiprism In geometry, the square antiprism is the second in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps... |
| 9 | 25.759986531 |  |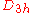
0 | 0 | 3 | 6 | 0 | 0 | 0 | 21 | 14 | 0 | 61.190° | triaugmented triangular prism Triaugmented triangular prism In geometry, the triaugmented triangular prism is one of the Johnson solids . As the name suggests, it can be constructed by attaching square pyramids to each of the three equatorial faces of the triangular prism... |
| 10 | 32.716949460 |  |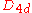
0 | 0 | 2 | 8 | 0 | 0 | 0 | 24 | 16 | 0 | 64.996° | gyroelongated square dipyramid Gyroelongated square dipyramid In geometry, the gyroelongated square bipyramid is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating an octahedron by inserting a square antiprism between its congruent halves... |
| 11 | 40.596450510 |  |
0.013219635 | 0 | 2 | 8 | 1 | 0 | 0 | 27 | 18 | 0 | 58.540° | |
| 12 | 49.165253058 |  |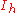
0 | 0 | 0 | 12 | 0 | 0 | 0 | 30 | 20 | 0 | 63.435° | icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
| 13 | 58.853230612 |  |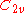
0.008820367 | 0 | 1 | 10 | 2 | 0 | 0 | 33 | 22 | 0 | 52.317° | |
| 14 | 69.306363297 |  |
0 | 0 | 0 | 12 | 2 | 0 | 0 | 36 | 24 | 0 | 52.866° | gyroelongated hexagonal dipyramid |
| 15 | 80.670244114 |  |
0 | 0 | 0 | 12 | 3 | 0 | 0 | 39 | 26 | 0 | 49.225° | |
| 16 | 92.911655302 |  |
0 | 0 | 0 | 12 | 4 | 0 | 0 | 42 | 28 | 0 | 48.936° | |
| 17 | 106.050404829 |  |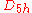
0 | 0 | 0 | 12 | 5 | 0 | 0 | 45 | 30 | 0 | 50.108° | |
| 18 | 120.084467447 |  |
0 | 0 | 2 | 8 | 8 | 0 | 0 | 48 | 32 | 0 | 47.534° | |
| 19 | 135.089467557 |  |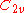
0.000135163 | 0 | 0 | 14 | 5 | 0 | 0 | 50 | 32 | 1 | 44.910° | |
| 20 | 150.881568334 |  |
0 | 0 | 0 | 12 | 8 | 0 | 0 | 54 | 36 | 0 | 46.093° | |
| 21 | 167.641622399 |  |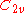
0.001406124 | 0 | 1 | 10 | 10 | 0 | 0 | 57 | 38 | 0 | 44.321° | |
| 22 | 185.287536149 |  |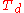
0 | 0 | 0 | 12 | 10 | 0 | 0 | 60 | 40 | 0 | 43.302° | |
| 23 | 203.930190663 |  |
0 | 0 | 0 | 12 | 11 | 0 | 0 | 63 | 42 | 0 | 41.481° | |
| 24 | 223.347074052 |  |
0 | 0 | 0 | 24 | 0 | 0 | 0 | 60 | 32 | 6 | 42.065° | snub cube Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... |
| 25 | 243.812760299 |  |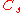
0.001021305 | 0 | 0 | 14 | 11 | 0 | 0 | 68 | 44 | 1 | 39.610° | |
| 26 | 265.133326317 |  |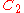
0.001919065 | 0 | 0 | 12 | 14 | 0 | 0 | 72 | 48 | 0 | 38.842° | |
| 27 | 287.302615033 |  |
0 | 0 | 0 | 12 | 15 | 0 | 0 | 75 | 50 | 0 | 39.940° | |
| 28 | 310.491542358 |  |
0 | 0 | 0 | 12 | 16 | 0 | 0 | 78 | 52 | 0 | 37.824° | |
| 29 | 334.634439920 |  |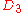
0 | 0 | 0 | 12 | 17 | 0 | 0 | 81 | 54 | 0 | 36.391° | |
| 30 | 359.603945904 |  |
0 | 0 | 0 | 12 | 18 | 0 | 0 | 84 | 56 | 0 | 36.942° | |
| 31 | 385.530838063 |  |
0.003204712 | 0 | 0 | 12 | 19 | 0 | 0 | 87 | 58 | 0 | 36.373° | |
| 32 | 412.261274651 |  |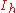
0 | 0 | 0 | 12 | 20 | 0 | 0 | 90 | 60 | 0 | 37.377° | |
| 33 | 440.204057448 |  |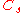
0.004356481 | 0 | 0 | 15 | 17 | 1 | 0 | 92 | 60 | 1 | 33.700° | |
| 34 | 468.904853281 |  |
0 | 0 | 0 | 12 | 22 | 0 | 0 | 96 | 64 | 0 | 33.273° | |
| 35 | 498.569872491 |  |
0.000419208 | 0 | 0 | 12 | 23 | 0 | 0 | 99 | 66 | 0 | 33.100° | |
| 36 | 529.122408375 |  |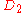
0 | 0 | 0 | 12 | 24 | 0 | 0 | 102 | 68 | 0 | 33.229° | |
| 37 | 560.618887731 |  |
0 | 0 | 0 | 12 | 25 | 0 | 0 | 105 | 70 | 0 | 32.332° | |
| 38 | 593.038503566 |  |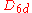
0 | 0 | 0 | 12 | 26 | 0 | 0 | 108 | 72 | 0 | 33.236° | |
| 39 | 626.389009017 |  |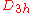
0 | 0 | 0 | 12 | 27 | 0 | 0 | 111 | 74 | 0 | 32.053° | |
| 40 | 660.675278835 |  |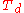
0 | 0 | 0 | 12 | 28 | 0 | 0 | 114 | 76 | 0 | 31.916° | |
| 41 | 695.916744342 |  |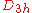
0 | 0 | 0 | 12 | 29 | 0 | 0 | 117 | 78 | 0 | 31.528° | |
| 42 | 732.078107544 |  |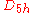
0 | 0 | 0 | 12 | 30 | 0 | 0 | 120 | 80 | 0 | 31.245° | |
| 43 | 769.190846459 |  |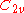
0.000399668 | 0 | 0 | 12 | 31 | 0 | 0 | 123 | 82 | 0 | 30.867° | |
| 44 | 807.174263085 |  |
0 | 0 | 0 | 24 | 20 | 0 | 0 | 120 | 72 | 6 | 31.258° | |
| 45 | 846.188401061 |  |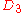
0 | 0 | 0 | 12 | 33 | 0 | 0 | 129 | 86 | 0 | 30.207° | |
| 46 | 886.167113639 |  |
0 | 0 | 0 | 12 | 34 | 0 | 0 | 132 | 88 | 0 | 29.790° | |
| 47 | 927.059270680 |  |
0.002482914 | 0 | 0 | 14 | 33 | 0 | 0 | 134 | 88 | 1 | 28.787° | |
| 48 | 968.713455344 |  |
0 | 0 | 0 | 24 | 24 | 0 | 0 | 132 | 80 | 6 | 29.690° | |
| 49 | 1011.557182654 |  |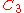
0.001529341 | 0 | 0 | 12 | 37 | 0 | 0 | 141 | 94 | 0 | 28.387° | |
| 50 | 1055.182314726 |  |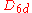
0 | 0 | 0 | 12 | 38 | 0 | 0 | 144 | 96 | 0 | 29.231° | |
| 51 | 1099.819290319 |  |
0 | 0 | 0 | 12 | 39 | 0 | 0 | 147 | 98 | 0 | 28.165° | |
| 52 | 1145.418964319 |  |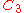
0.000457327 | 0 | 0 | 12 | 40 | 0 | 0 | 150 | 100 | 0 | 27.670° | |
| 53 | 1191.922290416 |  |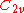
0.000278469 | 0 | 0 | 18 | 35 | 0 | 0 | 150 | 96 | 3 | 27.137° | |
| 54 | 1239.361474729 |  |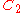
0.000137870 | 0 | 0 | 12 | 42 | 0 | 0 | 156 | 104 | 0 | 27.030° | |
| 55 | 1287.772720783 |  |
0.000391696 | 0 | 0 | 12 | 43 | 0 | 0 | 159 | 106 | 0 | 26.615° | |
| 56 | 1337.094945276 |  |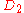
0 | 0 | 0 | 12 | 44 | 0 | 0 | 162 | 108 | 0 | 26.683° | |
| 57 | 1387.383229253 |  |
0 | 0 | 0 | 12 | 45 | 0 | 0 | 165 | 110 | 0 | 26.702° | |
| 58 | 1438.618250640 |  |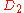
0 | 0 | 0 | 12 | 46 | 0 | 0 | 168 | 112 | 0 | 26.155° | |
| 59 | 1490.773335279 |  |
0.000154286 | 0 | 0 | 14 | 43 | 2 | 0 | 171 | 114 | 0 | 26.170° | |
| 60 | 1543.830400976 |  |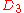
0 | 0 | 0 | 12 | 48 | 0 | 0 | 174 | 116 | 0 | 25.958° | |
| 61 | 1597.941830199 |  |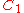
0.001091717 | 0 | 0 | 12 | 49 | 0 | 0 | 177 | 118 | 0 | 25.392° | |
| 62 | 1652.909409898 |  |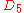
0 | 0 | 0 | 12 | 50 | 0 | 0 | 180 | 120 | 0 | 25.880° | |
| 63 | 1708.879681503 |  |
0 | 0 | 0 | 12 | 51 | 0 | 0 | 183 | 122 | 0 | 25.257° | |
| 64 | 1765.802577927 |  |
0 | 0 | 0 | 12 | 52 | 0 | 0 | 186 | 124 | 0 | 24.920° | |
| 65 | 1823.667960264 |  |
0.000399515 | 0 | 0 | 12 | 53 | 0 | 0 | 189 | 126 | 0 | 24.527° | |
| 66 | 1882.441525304 |  |
0.000776245 | 0 | 0 | 12 | 54 | 0 | 0 | 192 | 128 | 0 | 24.765° | |
| 67 | 1942.122700406 |  |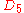
0 | 0 | 0 | 12 | 55 | 0 | 0 | 195 | 130 | 0 | 24.727° | |
| 68 | 2002.874701749 |  |
0 | 0 | 0 | 12 | 56 | 0 | 0 | 198 | 132 | 0 | 24.433° | |
| 69 | 2064.533483235 |  |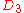
0 | 0 | 0 | 12 | 57 | 0 | 0 | 201 | 134 | 0 | 24.137° | |
| 70 | 2127.100901551 |  |
0 | 0 | 0 | 12 | 50 | 0 | 0 | 200 | 128 | 4 | 24.291° | |
| 71 | 2190.649906425 |  |
0.001256769 | 0 | 0 | 14 | 55 | 2 | 0 | 207 | 138 | 0 | 23.803° | |
| 72 | 2255.001190975 |  |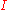
0 | 0 | 0 | 12 | 60 | 0 | 0 | 210 | 140 | 0 | 24.492° | |
| 73 | 2320.633883745 |  |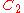
0.001572959 | 0 | 0 | 12 | 61 | 0 | 0 | 213 | 142 | 0 | 22.810° | |
| 74 | 2387.072981838 |  |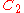
0.000641539 | 0 | 0 | 12 | 62 | 0 | 0 | 216 | 144 | 0 | 22.966° | |
| 75 | 2454.369689040 |  |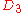
0 | 0 | 0 | 12 | 63 | 0 | 0 | 219 | 146 | 0 | 22.736° | |
| 76 | 2522.674871841 |  |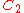
0.000943474 | 0 | 0 | 12 | 64 | 0 | 0 | 222 | 148 | 0 | 22.886° | |
| 77 | 2591.850152354 |  |
0 | 0 | 0 | 12 | 65 | 0 | 0 | 225 | 150 | 0 | 23.286° | |
| 78 | 2662.046474566 |  |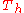
0 | 0 | 0 | 12 | 66 | 0 | 0 | 228 | 152 | 0 | 23.426° | |
| 79 | 2733.248357479 |  |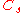
0.000702921 | 0 | 0 | 12 | 63 | 1 | 0 | 230 | 152 | 1 | 22.636° | |
| 80 | 2805.355875981 |  |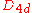
0 | 0 | 0 | 16 | 64 | 0 | 0 | 232 | 152 | 2 | 22.778° | |
| 81 | 2878.522829664 |  |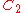
0.000194289 | 0 | 0 | 12 | 69 | 0 | 0 | 237 | 158 | 0 | 21.892° | |
| 82 | 2952.569675286 |  |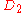
0 | 0 | 0 | 12 | 70 | 0 | 0 | 240 | 160 | 0 | 22.206° | |
| 83 | 3027.528488921 |  |
0.000339815 | 0 | 0 | 14 | 67 | 2 | 0 | 243 | 162 | 0 | 21.646° | |
| 84 | 3103.465124431 |  |
0.000401973 | 0 | 0 | 12 | 72 | 0 | 0 | 246 | 164 | 0 | 21.513° | |
| 85 | 3180.361442939 |  |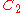
0.000416581 | 0 | 0 | 12 | 73 | 0 | 0 | 249 | 166 | 0 | 21.498° | |
| 86 | 3258.211605713 |  |
0.001378932 | 0 | 0 | 12 | 74 | 0 | 0 | 252 | 168 | 0 | 21.522° | |
| 87 | 3337.000750014 |  |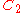
0.000754863 | 0 | 0 | 12 | 75 | 0 | 0 | 255 | 170 | 0 | 21.456° | |
| 88 | 3416.720196758 |  |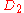
0 | 0 | 0 | 12 | 76 | 0 | 0 | 258 | 172 | 0 | 21.486° | |
| 89 | 3497.439018625 |  |
0.000070891 | 0 | 0 | 12 | 77 | 0 | 0 | 261 | 174 | 0 | 21.182° | |
| 90 | 3579.091222723 |  |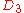
0 | 0 | 0 | 12 | 78 | 0 | 0 | 264 | 176 | 0 | 21.230° | |
| 91 | 3661.713699320 |  |
0.000033221 | 0 | 0 | 12 | 79 | 0 | 0 | 267 | 178 | 0 | 21.105° | |
| 92 | 3745.291636241 |  |
0 | 0 | 0 | 12 | 80 | 0 | 0 | 270 | 180 | 0 | 21.026° | |
| 93 | 3829.844338421 |  |
0.000213246 | 0 | 0 | 12 | 81 | 0 | 0 | 273 | 182 | 0 | 20.751° | |
| 94 | 3915.309269620 |  |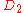
0 | 0 | 0 | 12 | 82 | 0 | 0 | 276 | 184 | 0 | 20.952° | |
| 95 | 4001.771675565 |  |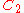
0.000116638 | 0 | 0 | 12 | 83 | 0 | 0 | 279 | 186 | 0 | 20.711° | |
| 96 | 4089.154010060 |  |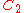
0.000036310 | 0 | 0 | 12 | 84 | 0 | 0 | 282 | 188 | 0 | 20.687° | |
| 97 | 4177.533599622 |  |
0.000096437 | 0 | 0 | 12 | 85 | 0 | 0 | 285 | 190 | 0 | 20.450° | |
| 98 | 4266.822464156 |  |
0.000112916 | 0 | 0 | 12 | 86 | 0 | 0 | 288 | 192 | 0 | 20.422° | |
| 99 | 4357.139163132 |  |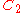
0.000156508 | 0 | 0 | 12 | 87 | 0 | 0 | 291 | 194 | 0 | 20.284° | |
| 100 | 4448.350634331 |  |
0 | 0 | 0 | 12 | 88 | 0 | 0 | 294 | 196 | 0 | 20.297° | |
| 101 | 4540.590051694 |  |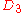
0 | 0 | 0 | 12 | 89 | 0 | 0 | 297 | 198 | 0 | 20.011° | |
| 102 | 4633.736565899 |  |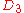
0 | 0 | 0 | 12 | 90 | 0 | 0 | 300 | 200 | 0 | 20.040° | |
| 103 | 4727.836616833 |  |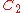
0.000201245 | 0 | 0 | 12 | 91 | 0 | 0 | 303 | 202 | 0 | 19.907° | |
| 104 | 4822.876522746 |  |
0 | 0 | 0 | 12 | 92 | 0 | 0 | 306 | 204 | 0 | 19.957° | |
| 105 | 4919.000637616 |  |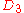
0 | 0 | 0 | 12 | 93 | 0 | 0 | 309 | 206 | 0 | 19.842° | |
| 106 | 5015.984595705 |  |
0 | 0 | 0 | 12 | 94 | 0 | 0 | 312 | 208 | 0 | 19.658° | |
| 107 | 5113.953547724 |  |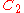
0.000064137 | 0 | 0 | 12 | 95 | 0 | 0 | 315 | 210 | 0 | 19.327° | |
| 108 | 5212.813507831 |  |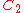
0.000432525 | 0 | 0 | 12 | 96 | 0 | 0 | 318 | 212 | 0 | 19.327° | |
| 109 | 5312.735079920 |  |
0.000647299 | 0 | 0 | 14 | 93 | 2 | 0 | 321 | 214 | 0 | 19.103° | |
| 110 | 5413.549294192 |  |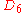
0 | 0 | 0 | 12 | 98 | 0 | 0 | 324 | 216 | 0 | 19.476° | |
| 111 | 5515.293214587 |  |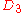
0 | 0 | 0 | 12 | 99 | 0 | 0 | 327 | 218 | 0 | 19.255° | |
| 112 | 5618.044882327 |  |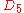
0 | 0 | 0 | 12 | 100 | 0 | 0 | 330 | 220 | 0 | 19.351° | |
| 113 | 5721.824978027 |  |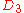
0 | 0 | 0 | 12 | 101 | 0 | 0 | 333 | 222 | 0 | 18.978° | |
| 114 | 5826.521572163 |  |
0.000149772 | 0 | 0 | 12 | 102 | 0 | 0 | 336 | 224 | 0 | 18.836° | |
| 115 | 5932.181285777 |  |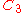
0.000049972 | 0 | 0 | 12 | 103 | 0 | 0 | 339 | 226 | 0 | 18.458° | |
| 116 | 6038.815593579 |  |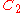
0.000259726 | 0 | 0 | 12 | 104 | 0 | 0 | 342 | 228 | 0 | 18.386° | |
| 117 | 6146.342446579 |  |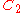
0.000127609 | 0 | 0 | 12 | 105 | 0 | 0 | 345 | 230 | 0 | 18.566° | |
| 118 | 6254.877027790 |  |
0.000332475 | 0 | 0 | 12 | 106 | 0 | 0 | 348 | 232 | 0 | 18.455° | |
| 119 | 6364.347317479 |  |
0.000685590 | 0 | 0 | 12 | 107 | 0 | 0 | 351 | 234 | 0 | 18.336° | |
| 120 | 6474.756324980 |  |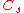
0.001373062 | 0 | 0 | 12 | 108 | 0 | 0 | 354 | 236 | 0 | 18.418° | |
| 121 | 6586.121949584 |  |
0.000838863 | 0 | 0 | 12 | 109 | 0 | 0 | 357 | 238 | 0 | 18.199° | |
| 122 | 6698.374499261 |  |
0 | 0 | 0 | 12 | 110 | 0 | 0 | 360 | 240 | 0 | 18.612° | |
| 123 | 6811.827228174 |  |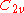
0.001939754 | 0 | 0 | 14 | 107 | 2 | 0 | 363 | 242 | 0 | 17.840° | |
| 124 | 6926.169974193 |  |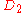
0 | 0 | 0 | 12 | 112 | 0 | 0 | 366 | 244 | 0 | 18.111° | |
| 125 | 7041.473264023 |  |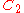
0.000088274 | 0 | 0 | 12 | 113 | 0 | 0 | 369 | 246 | 0 | 17.867° | |
| 126 | 7157.669224867 |  |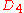
0 | 0 | 2 | 16 | 100 | 8 | 0 | 372 | 248 | 0 | 17.920° | |
| 127 | 7274.819504675 |  |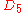
0 | 0 | 0 | 12 | 115 | 0 | 0 | 375 | 250 | 0 | 17.877° | |
| 128 | 7393.007443068 |  |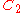
0.000054132 | 0 | 0 | 12 | 116 | 0 | 0 | 378 | 252 | 0 | 17.814° | |
| 129 | 7512.107319268 |  |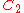
0.000030099 | 0 | 0 | 12 | 117 | 0 | 0 | 381 | 254 | 0 | 17.743° | |
| 130 | 7632.167378912 |  |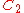
0.000025622 | 0 | 0 | 12 | 118 | 0 | 0 | 384 | 256 | 0 | 17.683° | |
| 131 | 7753.205166941 |  |
0.000305133 | 0 | 0 | 12 | 119 | 0 | 0 | 387 | 258 | 0 | 17.511° | |
| 132 | 7875.045342797 |  |
0 | 0 | 0 | 12 | 120 | 0 | 0 | 390 | 260 | 0 | 17.958° | |
| 133 | 7998.179212898 |  |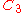
0.000591438 | 0 | 0 | 12 | 121 | 0 | 0 | 393 | 262 | 0 | 17.133° | |
| 134 | 8122.089721194 |  |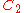
0.000470268 | 0 | 0 | 12 | 122 | 0 | 0 | 396 | 264 | 0 | 17.214° | |
| 135 | 8246.909486992 |  |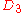
0 | 0 | 0 | 12 | 123 | 0 | 0 | 399 | 266 | 0 | 17.431° | |
| 136 | 8372.743302539 |  |
0 | 0 | 0 | 12 | 124 | 0 | 0 | 402 | 268 | 0 | 17.485° | |
| 137 | 8499.534494782 |  |
0 | 0 | 0 | 12 | 125 | 0 | 0 | 405 | 270 | 0 | 17.560° | |
| 138 | 8627.406389880 |  |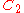
0.000473576 | 0 | 0 | 12 | 126 | 0 | 0 | 408 | 272 | 0 | 16.924° | |
| 139 | 8756.227056057 |  |
0.000404228 | 0 | 0 | 12 | 127 | 0 | 0 | 411 | 274 | 0 | 16.673° | |
| 140 | 8885.980609041 |  |
0.000630351 | 0 | 0 | 13 | 126 | 1 | 0 | 414 | 276 | 0 | 16.773° | |
| 141 | 9016.615349190 |  |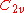
0.000376365 | 0 | 0 | 14 | 126 | 0 | 1 | 417 | 278 | 0 | 16.962° | |
| 142 | 9148.271579993 |  |
0.000550138 | 0 | 0 | 12 | 130 | 0 | 0 | 420 | 280 | 0 | 16.840° | |
| 143 | 9280.839851192 |  |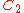
0.000255449 | 0 | 0 | 12 | 131 | 0 | 0 | 423 | 282 | 0 | 16.782° | |
| 144 | 9414.371794460 |  |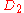
0 | 0 | 0 | 12 | 132 | 0 | 0 | 426 | 284 | 0 | 16.953° | |
| 145 | 9548.928837232 |  |
0.000094938 | 0 | 0 | 12 | 133 | 0 | 0 | 429 | 286 | 0 | 16.841° | |
| 146 | 9684.381825575 |  |
0 | 0 | 0 | 12 | 134 | 0 | 0 | 432 | 288 | 0 | 16.905° | |
| 147 | 9820.932378373 |  |
0.000636651 | 0 | 0 | 12 | 135 | 0 | 0 | 435 | 290 | 0 | 16.458° | |
| 148 | 9958.406004270 |  |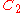
0.000203701 | 0 | 0 | 12 | 136 | 0 | 0 | 438 | 292 | 0 | 16.627° | |
| 149 | 10096.859907397 |  |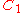
0.000638186 | 0 | 0 | 14 | 133 | 2 | 0 | 441 | 294 | 0 | 16.344° | |
| 150 | 10236.196436701 |  |
0 | 0 | 0 | 12 | 138 | 0 | 0 | 444 | 296 | 0 | 16.405° | |
| 151 | 10376.571469275 |  |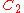
0.000153836 | 0 | 0 | 12 | 139 | 0 | 0 | 447 | 298 | 0 | 16.163° | |
| 152 | 10517.867592878 |  |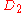
0 | 0 | 0 | 12 | 140 | 0 | 0 | 450 | 300 | 0 | 16.117° | |
| 153 | 10660.082748237 |  |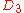
0 | 0 | 0 | 12 | 141 | 0 | 0 | 453 | 302 | 0 | 16.390° | |
| 154 | 10803.372421141 |  |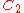
0.000735800 | 0 | 0 | 12 | 142 | 0 | 0 | 456 | 304 | 0 | 16.078° | |
| 155 | 10947.574692279 |  |
0.000603670 | 0 | 0 | 12 | 143 | 0 | 0 | 459 | 306 | 0 | 15.990° | |
| 156 | 11092.798311456 |  |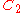
0.000508534 | 0 | 0 | 12 | 144 | 0 | 0 | 462 | 308 | 0 | 15.822° | |
| 157 | 11238.903041156 |  |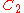
0.000357679 | 0 | 0 | 12 | 145 | 0 | 0 | 465 | 310 | 0 | 15.948° | |
| 158 | 11385.990186197 |  |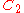
0.000921918 | 0 | 0 | 12 | 146 | 0 | 0 | 468 | 312 | 0 | 15.987° | |
| 159 | 11534.023960956 |  |
0.000381457 | 0 | 0 | 12 | 147 | 0 | 0 | 471 | 314 | 0 | 15.960° | |
| 160 | 11683.054805549 |  |
0 | 0 | 0 | 12 | 148 | 0 | 0 | 474 | 316 | 0 | 15.961° | |
| 161 | 11833.084739465 |  |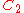
0.000056447 | 0 | 0 | 12 | 149 | 0 | 0 | 477 | 318 | 0 | 15.810° | |
| 162 | 11984.050335814 |  |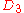
0 | 0 | 0 | 12 | 150 | 0 | 0 | 480 | 320 | 0 | 15.813° | |
| 163 | 12136.013053220 |  |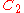
0.000120798 | 0 | 0 | 12 | 151 | 0 | 0 | 483 | 322 | 0 | 15.675° | |
| 164 | 12288.930105320 |  |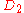
0 | 0 | 0 | 12 | 152 | 0 | 0 | 486 | 324 | 0 | 15.655° | |
| 165 | 12442.804451373 |  |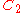
0.000091119 | 0 | 0 | 12 | 153 | 0 | 0 | 489 | 326 | 0 | 15.651° | |
| 166 | 12597.649071323 |  |
0 | 0 | 0 | 16 | 146 | 4 | 0 | 492 | 328 | 0 | 15.607° | |
| 167 | 12753.469429750 |  |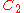
0.000097382 | 0 | 0 | 12 | 155 | 0 | 0 | 495 | 330 | 0 | 15.600° | |
| 168 | 12910.212672268 |  |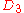
0 | 0 | 0 | 12 | 156 | 0 | 0 | 498 | 332 | 0 | 15.655° | |
| 169 | 13068.006451127 |  |
0.000068102 | 0 | 0 | 13 | 155 | 1 | 0 | 501 | 334 | 0 | 15.537° | |
| 170 | 13226.681078541 |  |
0 | 0 | 0 | 12 | 158 | 0 | 0 | 504 | 336 | 0 | 15.569° | |
| 171 | 13386.355930717 |  |
0 | 0 | 0 | 12 | 159 | 0 | 0 | 507 | 338 | 0 | 15.497° | |
| 172 | 13547.018108787 |  |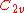
0.000547291 | 0 | 0 | 14 | 156 | 2 | 0 | 510 | 340 | 0 | 15.292° | |
| 173 | 13708.635243034 |  |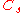
0.000286544 | 0 | 0 | 12 | 161 | 0 | 0 | 513 | 342 | 0 | 15.225° | |
| 174 | 13871.187092292 |  |
0 | 0 | 0 | 12 | 162 | 0 | 0 | 516 | 344 | 0 | 15.366° | |
| 175 | 14034.781306929 |  |
0.000026686 | 0 | 0 | 12 | 163 | 0 | 0 | 519 | 346 | 0 | 15.252° | |
| 176 | 14199.354775632 |  |
0.000283978 | 0 | 0 | 12 | 164 | 0 | 0 | 522 | 348 | 0 | 15.101° | |
| 177 | 14364.837545298 |  |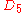
0 | 0 | 0 | 12 | 165 | 0 | 0 | 525 | 350 | 0 | 15.269° | |
| 178 | 14531.309552587 |  |
0 | 0 | 0 | 12 | 166 | 0 | 0 | 528 | 352 | 0 | 15.145° | |
| 179 | 14698.754594220 |  |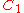
0.000125113 | 0 | 0 | 13 | 165 | 1 | 0 | 531 | 354 | 0 | 14.968° | |
| 180 | 14867.099927525 |  |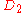
0 | 0 | 0 | 12 | 168 | 0 | 0 | 534 | 356 | 0 | 15.067° | |
| 181 | 15036.467239769 |  |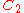
0.000304193 | 0 | 0 | 12 | 169 | 0 | 0 | 537 | 358 | 0 | 15.002° | |
| 182 | 15206.730610906 |  |
0 | 0 | 0 | 12 | 170 | 0 | 0 | 540 | 360 | 0 | 15.155° | |
| 183 | 15378.166571028 |  |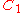
0.000467899 | 0 | 0 | 12 | 171 | 0 | 0 | 543 | 362 | 0 | 14.747° | |
| 184 | 15550.421450311 |  |
0 | 0 | 0 | 12 | 172 | 0 | 0 | 546 | 364 | 0 | 14.932° | |
| 185 | 15723.720074072 |  |
0.000389762 | 0 | 0 | 12 | 173 | 0 | 0 | 549 | 366 | 0 | 14.775° | |
| 186 | 15897.897437048 |  |
0.000389762 | 0 | 0 | 12 | 174 | 0 | 0 | 552 | 368 | 0 | 14.739° | |
| 187 | 16072.975186320 |  |
0 | 0 | 0 | 12 | 175 | 0 | 0 | 555 | 370 | 0 | 14.848° | |
| 188 | 16249.222678879 |  |
0 | 0 | 0 | 12 | 176 | 0 | 0 | 558 | 372 | 0 | 14.740° | |
| 189 | 16426.371938862 |  |
0.000020732 | 0 | 0 | 12 | 177 | 0 | 0 | 561 | 374 | 0 | 14.671° | |
| 190 | 16604.428338501 |  |
0.000586804 | 0 | 0 | 12 | 178 | 0 | 0 | 564 | 376 | 0 | 14.501° | |
| 191 | 16783.452219362 |  |
0.001129202 | 0 | 0 | 13 | 177 | 1 | 0 | 567 | 378 | 0 | 14.195° | |
| 192 | 16963.338386460 |  |
0 | 0 | 0 | 12 | 180 | 0 | 0 | 570 | 380 | 0 | 14.819° | |
| 193 | 17144.564740880 |  |
0.000985192 | 0 | 0 | 12 | 181 | 0 | 0 | 573 | 382 | 0 | 14.144° | |
| 194 | 17326.616136471 |  |
0.000322358 | 0 | 0 | 12 | 182 | 0 | 0 | 576 | 384 | 0 | 14.350° | |
| 195 | 17509.489303930 |  |
0 | 0 | 0 | 12 | 183 | 0 | 0 | 579 | 386 | 0 | 14.375° | |
| 196 | 17693.460548082 |  |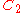
0.000315907 | 0 | 0 | 12 | 184 | 0 | 0 | 582 | 388 | 0 | 14.251° | |
| 197 | 17878.340162571 |  |
0 | 0 | 0 | 12 | 185 | 0 | 0 | 585 | 390 | 0 | 14.147° | |
| 198 | 18064.262177195 |  |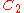
0.000011149 | 0 | 0 | 12 | 186 | 0 | 0 | 588 | 392 | 0 | 14.237° | |
| 199 | 18251.082495640 |  |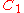
0.000534779 | 0 | 0 | 12 | 187 | 0 | 0 | 591 | 394 | 0 | 14.153° | |
| 200 | 18438.842717530 |  |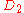
0 | 0 | 0 | 12 | 188 | 0 | 0 | 594 | 396 | 0 | 14.222° | |
| 201 | 18627.591226244 |  |
0.001048859 | 0 | 0 | 13 | 187 | 1 | 0 | 597 | 398 | 0 | 13.830° | |
| 202 | 18817.204718262 |  |
0 | 0 | 0 | 12 | 190 | 0 | 0 | 600 | 400 | 0 | 14.189° | |
| 203 | 19007.981204580 |  |
0.000600343 | 0 | 0 | 12 | 191 | 0 | 0 | 603 | 402 | 0 | 13.977° | |
| 204 | 19199.540775603 |  |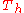
0 | 0 | 0 | 12 | 192 | 0 | 0 | 606 | 404 | 0 | 14.291° | |
| 212 | 20768.053085964 |  |
0 | 0 | 0 | 12 | 200 | 0 | 0 | 630 | 420 | 0 | 14.118° | |
| 214 | 21169.910410375 |  |
0 | 0 | 0 | 12 | 202 | 0 | 0 | 636 | 424 | 0 | 13.771° | |
| 216 | 21575.596377869 |  |
0 | 0 | 0 | 12 | 204 | 0 | 0 | 642 | 428 | 0 | 13.735° | |
| 217 | 21779.856080418 |  |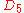
0 | 0 | 0 | 12 | 205 | 0 | 0 | 645 | 430 | 0 | 13.902° | |
| 232 | 24961.252318934 |  |
0 | 0 | 0 | 12 | 220 | 0 | 0 | 690 | 460 | 0 | 13.260° | |
| 255 | 30264.424251281 |  |
0 | 0 | 0 | 12 | 243 | 0 | 0 | 759 | 506 | 0 | 12.565° | |
| 256 | 30506.687515847 |  |
0 | 0 | 0 | 12 | 244 | 0 | 0 | 762 | 508 | 0 | 12.572° | |
| 257 | 30749.941417346 |  |
0 | 0 | 0 | 12 | 245 | 0 | 0 | 765 | 510 | 0 | 12.672° | |
| 272 | 34515.193292681 |  |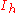
0 | 0 | 0 | 12 | 260 | 0 | 0 | 810 | 540 | 0 | 12.335° | |
| 282 | 37147.294418462 |  |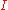
0 | 0 | 0 | 12 | 270 | 0 | 0 | 840 | 560 | 0 | 12.166° | |
| 292 | 39877.008012909 |  |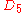
0 | 0 | 0 | 12 | 280 | 0 | 0 | 870 | 580 | 0 | 11.857° | |
| 306 | 43862.569780797 |  |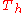
0 | 0 | 0 | 12 | 294 | 0 | 0 | 912 | 608 | 0 | 11.628° | |
| 312 | 45629.313804002 |  |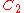
0.000306163 | 0 | 0 | 12 | 300 | 0 | 0 | 930 | 620 | 0 | 11.299° | |
| 315 | 46525.825643432 |  |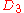
0 | 0 | 0 | 12 | 303 | 0 | 0 | 939 | 626 | 0 | 11.337° | |
| 317 | 47128.310344520 |  |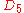
0 | 0 | 0 | 12 | 305 | 0 | 0 | 945 | 630 | 0 | 11.423° | |
| 318 | 47431.056020043 |  |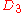
0 | 0 | 0 | 12 | 306 | 0 | 0 | 948 | 632 | 0 | 11.219° | |
| 334 | 52407.728127822 |  |
0 | 0 | 0 | 12 | 322 | 0 | 0 | 996 | 664 | 0 | 11.058° | |
| 348 | 56967.472454334 |  |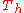
0 | 0 | 0 | 12 | 336 | 0 | 0 | 1038 | 692 | 0 | 10.721° | |
| 357 | 59999.922939598 |  |
0 | 0 | 0 | 12 | 345 | 0 | 0 | 1065 | 710 | 0 | 10.728° | |
| 358 | 60341.830924588 |  |
0 | 0 | 0 | 12 | 346 | 0 | 0 | 1068 | 712 | 0 | 10.647° | |
| 372 | 65230.027122557 |  |
0 | 0 | 0 | 12 | 360 | 0 | 0 | 1110 | 740 | 0 | 10.531° | |
| 382 | 68839.426839215 |  |
0 | 0 | 0 | 12 | 370 | 0 | 0 | 1140 | 760 | 0 | 10.379° | |
| 390 | 71797.035335953 |  |
0 | 0 | 0 | 12 | 378 | 0 | 0 | 1164 | 776 | 0 | 10.222° | |
| 392 | 72546.258370889 |  |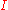
0 | 0 | 0 | 12 | 380 | 0 | 0 | 1170 | 780 | 0 | 10.278° | |
| 400 | 75582.448512213 |  |
0 | 0 | 0 | 12 | 388 | 0 | 0 | 1194 | 796 | 0 | 10.068° | |
| 402 | 76351.192432673 |  |
0 | 0 | 0 | 12 | 390 | 0 | 0 | 1200 | 800 | 0 | 10.099° | |
| 432 | 88353.709681956 |  |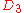
0 | 0 | 0 | 24 | 396 | 12 | 0 | 1290 | 860 | 0 | 9.556° | |
| 448 | 95115.546986209 |  |
0 | 0 | 0 | 24 | 412 | 12 | 0 | 1338 | 892 | 0 | 9.322° | |
| 460 | 100351.763108673 |  |
0 | 0 | 0 | 24 | 424 | 12 | 0 | 1374 | 916 | 0 | 9.297° | |
| 468 | 103920.871715127 |  |
0 | 0 | 0 | 24 | 432 | 12 | 0 | 1398 | 932 | 0 | 9.120° | |
| 470 | 104822.886324279 |  |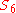
0 | 0 | 0 | 24 | 434 | 12 | 0 | 1404 | 936 | 0 | 9.059° |