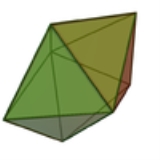
Pentagonal dipyramid
Encyclopedia
In geometry
, the pentagonal bipyramid
(or dipyramid) is third of the infinite set of face-transitive bipyramids.
Each bipyramid is the dual
of a uniform prism
.
If the faces are equilateral triangles, it is a deltahedron
and a Johnson solid
(J13). It can be seen as two pentagonal pyramid
s (J2) connected by their bases.
Although it is face-transitive, it is not a Platonic solid
because some vertices
have four face
s meeting and others have five faces.
The pentagonal dipyramid is 4-connected
, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial
well-covered
polyhedra, meaning that all of the maximal independent set
s of its vertices have the same size. The other three polyhedra with this property are the regular octahedron, the snub disphenoid
, and an irregular polyhedron with 12 vertices and 20 triangular faces.
, with 7 faces: 5 rectangular faces and 2 pentagons.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the pentagonal bipyramid
Bipyramid
An n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.The...
(or dipyramid) is third of the infinite set of face-transitive bipyramids.
Each bipyramid is the dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of a uniform prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
.
If the faces are equilateral triangles, it is a deltahedron
Deltahedron
A deltahedron is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta , which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces...
and a Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
(J13). It can be seen as two pentagonal pyramid
Pentagonal pyramid
In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point . Like any pyramid, it is self-dual....
s (J2) connected by their bases.
Although it is face-transitive, it is not a Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
because some vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
have four face
Face
The face is a central sense organ complex, for those animals that have one, normally on the ventral surface of the head, and can, depending on the definition in the human case, include the hair, forehead, eyebrow, eyelashes, eyes, nose, ears, cheeks, mouth, lips, philtrum, temple, teeth, skin, and...
s meeting and others have five faces.
The pentagonal dipyramid is 4-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial
Simplicial polytope
In geometry, a simplicial polytope is a d-polytope whose facets are all simplices.For example, a simplicial polyhedron contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph....
well-covered
Well-covered graph
In graph theory, a well-covered graph is an undirected graph in which every minimal vertex cover has the same size as every other minimal vertex cover. Well-covered graphs were defined and first studied by .-Definitions:...
polyhedra, meaning that all of the maximal independent set
Maximal independent set
In graph theory, a maximal independent set or maximal stable set is an independent set that is not a subset of any other independent set. That is, it is a set S such that every edge of the graph has at least one endpoint not in S and every vertex not in S has at least one neighbor in S...
s of its vertices have the same size. The other three polyhedra with this property are the regular octahedron, the snub disphenoid
Snub disphenoid
In geometry, the snub disphenoid is one of the Johnson solids . It is a three-dimensional solid that has only equilateral triangles as faces, and is therefore a deltahedron. It is not a regular polyhedron because some vertices have four faces and others have five...
, and an irregular polyhedron with 12 vertices and 20 triangular faces.

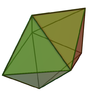
Dual polyhedron
The dual of the Johnson solid pentagonal bipyramid is the pentagonal prismPentagonal prism
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :...
, with 7 faces: 5 rectangular faces and 2 pentagons.
| Dual pentagonal bipyramid | Net of dual |
|---|---|

