.gif)
Clasper (mathematics)
Encyclopedia
In the mathematical field of low-dimensional topology
, a clasper is a surface
(with extra structure) in a 3-manifold
on which surgery
can be performed.
, links
, and 3-manifold
s were found during the 1980s. The study of these new `quantum' invariants expanded rapidly into a sub-discipline of low-dimensional topology called quantum topology. A quantum invariant is typically constructed from two ingredients: a formal sum of Jacobi diagrams (which carry a Lie algebra structure), and a representation of a ribbon Hopf algebra
such as a quantum group
. It is not clear a-priori why either of these ingredients should have anything to do with low-dimensional topology. Thus one of the main problems in quantum topology has been to interpret quantum invariants topologically.
The theory of claspers comes to provide such an interpretation. A clasper, like a framed link, is an embedded
topological object in a 3-manifold on which one can perform surgery
. In fact, clasper calculus can be thought of as a variant of Kirby calculus
on which only certain specific types of framed links are allowed. Claspers may also be interpreted algebraically, as a diagram calculus for the braided strict monoidal category Cob of oriented
connected surfaces with connected boundary. Additionally, most crucially, claspers may be roughly viewed as a topological realization of Jacobi diagrams, which are purely combinatorial
objects. This explains the Lie algebra
structure of the graded vector space
of Jacobi diagrams in terms of the Hopf algebra structure of Cob.
 is a compact surface embedded in the interior of a 3-manifold
is a compact surface embedded in the interior of a 3-manifold  equipped with a decomposition into two subsurfaces
equipped with a decomposition into two subsurfaces  and
and  , whose connected components are called the constituents and the edges of
, whose connected components are called the constituents and the edges of  correspondingly. Each edge of
correspondingly. Each edge of  is a band joining two constituents to one another, or joining one constituent to itself. There are four types of constituents: leaves, disk-leaves, nodes, and boxes.
is a band joining two constituents to one another, or joining one constituent to itself. There are four types of constituents: leaves, disk-leaves, nodes, and boxes.
Clasper surgery is most easily defined (after elimination of nodes, boxes, and disk-leaves as described below) as surgery along a link associated to the clasper by replacing each leaf with its core, and replacing each edge by a right Hopf link.

Habiro found 12 moves which relate claspers along which surgery gives the same result. These moves form the core of clasper calculus, and give considerable power to the theory as a theorem-proving tool.

Two knots, links, or 3-manifolds are said to be 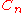 -equivalent if they are related by
-equivalent if they are related by 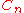 -moves, which are the local moves induced by surgeries on a simple tree claspers without boxes or disk-leaves and with
-moves, which are the local moves induced by surgeries on a simple tree claspers without boxes or disk-leaves and with  leaves.
leaves.
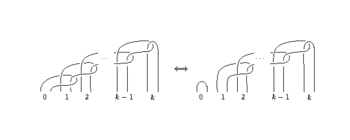 For a link
For a link  , a
, a 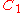 -move is a crossing change. A
-move is a crossing change. A 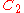 -move is a Delta move. Most applications of claspers use only
-move is a Delta move. Most applications of claspers use only 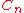 -moves.
-moves.
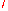 and a non-negative integer
and a non-negative integer 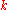 , the following conditions are equivalent:
, the following conditions are equivalent:
The corresponding statement is false for links.
Low-dimensional topology
In mathematics, low-dimensional topology is the branch of topology that studies manifolds of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. It can be regarded as a part of geometric topology.A number of...
, a clasper is a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
(with extra structure) in a 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
on which surgery
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
can be performed.
Motivation
Beginning with the Jones polynomial, infinitely many new invariants of knotsKnot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
, links
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
, and 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s were found during the 1980s. The study of these new `quantum' invariants expanded rapidly into a sub-discipline of low-dimensional topology called quantum topology. A quantum invariant is typically constructed from two ingredients: a formal sum of Jacobi diagrams (which carry a Lie algebra structure), and a representation of a ribbon Hopf algebra
Ribbon Hopf algebra
A ribbon Hopf algebra is a quasitriangular Hopf algebra which possess an invertible central element \nu more commonly known as the ribbon element, such that the following conditions hold:...
such as a quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
. It is not clear a-priori why either of these ingredients should have anything to do with low-dimensional topology. Thus one of the main problems in quantum topology has been to interpret quantum invariants topologically.
The theory of claspers comes to provide such an interpretation. A clasper, like a framed link, is an embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
topological object in a 3-manifold on which one can perform surgery
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
. In fact, clasper calculus can be thought of as a variant of Kirby calculus
Kirby calculus
In mathematics, the Kirby calculus in geometric topology, named after Robion Kirby, is a method for modifying framed links in the 3-sphere using a finite set of moves, the Kirby moves...
on which only certain specific types of framed links are allowed. Claspers may also be interpreted algebraically, as a diagram calculus for the braided strict monoidal category Cob of oriented
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
connected surfaces with connected boundary. Additionally, most crucially, claspers may be roughly viewed as a topological realization of Jacobi diagrams, which are purely combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
objects. This explains the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
structure of the graded vector space
Graded vector space
In mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
of Jacobi diagrams in terms of the Hopf algebra structure of Cob.
Definition
A clasper is a compact surface embedded in the interior of a 3-manifold
is a compact surface embedded in the interior of a 3-manifold  equipped with a decomposition into two subsurfaces
equipped with a decomposition into two subsurfaces  and
and  , whose connected components are called the constituents and the edges of
, whose connected components are called the constituents and the edges of  correspondingly. Each edge of
correspondingly. Each edge of  is a band joining two constituents to one another, or joining one constituent to itself. There are four types of constituents: leaves, disk-leaves, nodes, and boxes.
is a band joining two constituents to one another, or joining one constituent to itself. There are four types of constituents: leaves, disk-leaves, nodes, and boxes.Clasper surgery is most easily defined (after elimination of nodes, boxes, and disk-leaves as described below) as surgery along a link associated to the clasper by replacing each leaf with its core, and replacing each edge by a right Hopf link.

Clasper calculus
The following are the graphical conventions used when drawing claspers (and may be viewed as a definition for boxes, nodes, and disk-leaves):Habiro found 12 moves which relate claspers along which surgery gives the same result. These moves form the core of clasper calculus, and give considerable power to the theory as a theorem-proving tool.

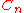 -equivalence
-equivalence
Two knots, links, or 3-manifolds are said to be 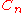 -equivalent if they are related by
-equivalent if they are related by 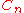 -moves, which are the local moves induced by surgeries on a simple tree claspers without boxes or disk-leaves and with
-moves, which are the local moves induced by surgeries on a simple tree claspers without boxes or disk-leaves and with  leaves.
leaves.
 , a
, a 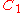 -move is a crossing change. A
-move is a crossing change. A 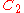 -move is a Delta move. Most applications of claspers use only
-move is a Delta move. Most applications of claspers use only 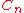 -moves.
-moves.Main results
For two knots K and K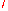 and a non-negative integer
and a non-negative integer 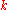 , the following conditions are equivalent:
, the following conditions are equivalent:-
 and K
and K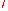 are not distinguished by any invariant of type
are not distinguished by any invariant of type 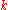 .
. -
 and K
and K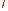 are
are 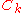 -equivalent.
-equivalent.
The corresponding statement is false for links.

