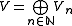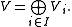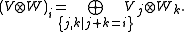Graded vector space
Encyclopedia
In mathematics
, a graded vector space is a type of vector space
that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.
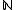be the set of non-negative integers. An 
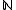-graded vector space, often called simply a graded vector space without the prefix 
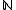, is a vector space V which decomposes into a direct sum of the form
where each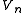
is a vector space. For a given n the elements of 
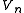are then called homogeneous elements of degree n.
Graded vector spaces are common. For example the set of all polynomial
s in one variable form a graded vector space, where the homogeneous elements of degree n are exactly the linear combinations of monomials of degree n.
Therefore, an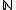
-graded vector space, as defined above, is just an I-graded vector space where the set I is 
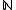(the set of natural number
s).
The case where I is the ring
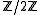(the elements 0 and 1) is particularly important in physics
. A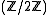
-graded vector space is also known as a supervector space.
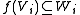for all i in I.
When I is a commutative monoid
(such as the natural numbers), then one may more generally define linear maps that are homogeneous of any degree i in I by the property
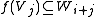for all j in I,
where "+" denotes the monoid operation. If moreover I satisfies the cancellation property
so that it can be embedded into a commutative group A which it generates (for instance the integer
s if I is the natural numbers), then one may also define linear maps that are homogeneous of degree i in A by the same property (but now "+" denotes the group operation in A). In particular for i in I a linear map will be homogeneous of degree −i if
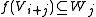for all j in I, while
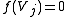if j−i is not in I.
Just as the set of linear maps from a vector space to itself forms an associative algebra
(the algebra of endomorphism
s of the vector space), the sets of homogeneous linear maps from a space to itself, either restricting degrees to I or allowing any degrees in the group A, form associative graded algebra
s over those index sets.
Given two I-graded vector spaces V and W, their direct sum has underlying vector space V ⊕ W with gradationi = Vi ⊕ Wi .
If I is a semigroup
, then the tensor product of two I-graded vector spaces V and W is another I-graded vector space,
with gradation
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a graded vector space is a type of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.
N-graded vector spaces
Let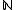 be the set of non-negative integers. An 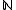-graded vector space, often called simply a graded vector space without the prefix 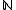, is a vector space V which decomposes into a direct sum of the form
where each
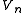is a vector space. For a given n the elements of 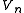are then called homogeneous elements of degree n.Graded vector spaces are common. For example the set of all polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in one variable form a graded vector space, where the homogeneous elements of degree n are exactly the linear combinations of monomials of degree n.
General I-graded vector spaces
The subspaces of a graded vector space need not be indexed by the set of natural numbers, and may be indexed by the elements of any set I. An I-graded vector space V is a vector space that can be written as a direct sum of subspaces indexed by elements i of set I:
Therefore, an
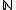-graded vector space, as defined above, is just an I-graded vector space where the set I is 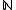(the set of natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s).
The case where I is the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
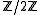(the elements 0 and 1) is particularly important in physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. A
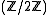-graded vector space is also known as a supervector space.Linear maps
For general index sets I, a linear map between two I-graded vector spaces f:V→W is called a graded linear map if it preserves the grading of homogeneous elements: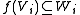 for all i in I.When I is a commutative monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
(such as the natural numbers), then one may more generally define linear maps that are homogeneous of any degree i in I by the property
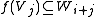for all j in I,where "+" denotes the monoid operation. If moreover I satisfies the cancellation property
Cancellation property
In mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
so that it can be embedded into a commutative group A which it generates (for instance the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s if I is the natural numbers), then one may also define linear maps that are homogeneous of degree i in A by the same property (but now "+" denotes the group operation in A). In particular for i in I a linear map will be homogeneous of degree −i if
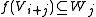for all j in I, while 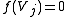if j−i is not in I.Just as the set of linear maps from a vector space to itself forms an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
(the algebra of endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s of the vector space), the sets of homogeneous linear maps from a space to itself, either restricting degrees to I or allowing any degrees in the group A, form associative graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
s over those index sets.
Operations on graded vector spaces
Some operations on vector spaces can be defined for graded vector spaces as well.Given two I-graded vector spaces V and W, their direct sum has underlying vector space V ⊕ W with gradationi = Vi ⊕ Wi .
If I is a semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
, then the tensor product of two I-graded vector spaces V and W is another I-graded vector space,
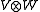with gradation
See also
- Super vector spaceSuper vector spaceIn mathematics, a super vector space is another name for a Z2-graded vector space, that is, a vector space over a field K with a given decompositionV=V_0\oplus V_1....
- Graded algebraGraded algebraIn mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
- Hilbert–Poincaré seriesHilbert–Poincaré seriesIn mathematics, and in particular in the field of algebra, a Hilbert–Poincaré series , named after David Hilbert and Henri Poincaré, is an adaptation of the notion of dimension to the context of graded algebraic structures...
- ComoduleComoduleIn mathematics, a comodule or corepresentation is a concept dual to a module. The definition of a comodule over a coalgebra is formed by dualizing the definition of a module over an associative algebra.-Formal definition:...