
Comodule
Encyclopedia
In mathematics
, a comodule or corepresentation is a concept dual
to a module
. The definition of a comodule over a coalgebra
is formed by dualizing the definition of a module over an associative algebra
.
, and C be a coalgebra
over K. A (right) comodule over C is a K-vector space
M together with a linear map
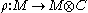
such that
where Δ is the comultiplication for C, and ε is the counit.
Note that in the second rule we have identified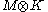 with
with 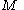 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a comodule or corepresentation is a concept dual
Dual
Dual may refer to:* Dual , a notion of paired concepts that mirror one another** Dual , a formalization of mathematical duality** . . ...
to a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. The definition of a comodule over a coalgebra
Coalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
is formed by dualizing the definition of a module over an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
.
Formal definition
Let K be a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, and C be a coalgebra
Coalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
over K. A (right) comodule over C is a K-vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
M together with a linear map
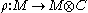
such that
-

-
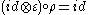 ,
,
where Δ is the comultiplication for C, and ε is the counit.
Note that in the second rule we have identified
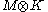 with
with 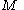 .
.Examples
- A coalgebra is a comodule over itself.
- If M is a finite-dimensional module over a finite-dimensional K-algebra A, then the set of linear functionLinear functionIn mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
s from A to K forms a coalgebra, and the set of linear functions from M to K forms a comodule over that coalgebra.
- A graded vector spaceGraded vector spaceIn mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
V can be made into a comodule. Let I be the index setIndex setIn mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
for the graded vector space, and let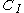 be the vector space with basis
be the vector space with basis 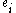 for
for  . We turn
. We turn  into a coalgebra and V into a
into a coalgebra and V into a 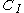 -comodule, as follows:
-comodule, as follows:
-
- Let the comultiplication on
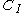 be given by
be given by 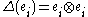 .
. - Let the counit on
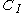 be given by
be given by  .
. - Let the map
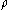 on V be given by
on V be given by 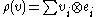 , where
, where  is the i-th homogeneous piece of
is the i-th homogeneous piece of  .
.
- Let the comultiplication on

