Classical modular curve
Encyclopedia
In number theory
, the classical modular curve is an irreducible plane algebraic curve
given by an equation
where for the j-invariant
j(τ),
is a point on the curve. The curve is sometimes called X0(n), though often that is used for the abstract algebraic curve
for which there exist various models. A related object is the classical modular polynomial, a polynomial in one variable defined as Φn(x, x).
The classical modular curve, which we will call X0(n), is of degree greater than or equal to 2n when n>1, with equality if and only if n is a prime. The polynomial Φn has integer coefficients, and hence is defined over every field. However, the coefficients are sufficiently large that computational work with the curve can be difficult. As a polynomial in x with coefficients in Z[y], it has degree ψ(n), where ψ is the Dedekind psi function. Since Φn(x, y) = Φn(y, x), X0(n) is symmetrical around the line y=x, and has singular points at the repeated roots of the classical modular polynomial, where it crosses itself in the complex plane. These are not the only singularities, and in particular when n>2, there are two singularites at infinity, where x=0, y=∞ and x=∞, y=0, which have only one branch and hence have a knot invariant which is a true knot, and not just a link.
zero, and hence can be parametrized by rational functions. The simplest nontrivial example is X0(2), where if
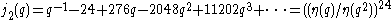
is (up to the constant term) the McKay–Thompson series for the class 2B of the Monster
, and η is the Dedekind eta function
, then
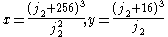
parametrizes X0(2) in terms of rational functions of j2. It is not necessary to actually compute j2 to use this parametrization; it can be taken as an arbitrary parameter.
is a modular curve
. The famous modularity theorem tells us that all elliptic curve
s over Q are modular.
Mappings also arise in connection with X0(n) since points on it correspond to n-isogenous pairs of elliptic curves. Two elliptic curves are isogenous if there is a morphism of varieties (defined by a rational map) between the curves which is also a group homomorphism, respecting the group law on the elliptic curves, and hence which sends the point at infinity (serving as the identity of the group law) to the point at infinity. The isogenies with cyclic kernel of degree n, the cyclic isogenies, correspond to points on X0(n).
When X0(n) has genus one, it will itself be isomorphic to an elliptic curve, which will have the same j-invariant
. For instance, X0(11) has j-invariant -122023936/161051 = - 21211-5313, and is isomorphic to the curve y2+y = x3-x2-10x-20. If we substitute this value of j for y in X0(5), we obtain two rational roots and a factor of degree four. The two rational roots correspond to isomorphism classes of curves with rational coefficients which are 5-isogenous to the above curve, but not isomorphic, having a different function field.
Specifically, we have the six rational points x=-122023936/161051, y=-4096/11, x=-122023936/161051, y=-52893159101157376/11, and x=-4096/11, y=-52893159101157376/11, plus the three points exchanging x and y, all on X0(5), corresponding to the six isogenies between these three curves. If in the curve y2+y = x3-x2-10x-20 isomorphic to X0(11) we substitute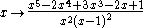
and
and factor, we get an extraneous factor of a rational function of x, and the curve y^2+y=x^3-x^2, with j-invariant -4096/11. Hence both curves are modular of level 11, having mappings from X0(11).
By a theorem of Henri Carayol, if an elliptic curve E is modular then its conductor, an isogeny invariant described originally in terms of cohomology
,
is the smallest integer n such that there exists a rational mapping φ:X0(n) → E. Since we now know all elliptic curves over Q are modular, we also know that the conductor is simply the level n of its minimal modular parametrization.
. Considered as a polynomial in x with coefficients in Z[y], the modular equation Φ0(n) is a polynomial of degree ψ(n) in x, whose roots generate a Galois extension
of Q(y). In the case of X0(p) with p prime, where the characteristic
of the field is not p, the Galois group
of
is PGL2(p), the projective general linear group
of linear fractional transformations of the projective line
of the field of p elements, which has p+1 points, the degree of X0(p).
This extension contains an algebraic extension
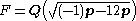
of Q. If we extend the field of constants to be F, we now have an extension with Galois group PSL2(p), the projective special linear group
of the field with p elements, which is a finite simple group. By specializing y to a specific field element, we can, outside of a thin set, obtain an infinity of examples of fields with Galois group PSL2(p) over F, and PGL2(p) over Q.
When n is not a prime, the Galois groups can be analyzed in terms of the factors of n as a wreath product
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the classical modular curve is an irreducible plane algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
given by an equation
- Φn(x, y)=0,
where for the j-invariant
J-invariant
In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
j(τ),
- x=j(n τ), y=j(τ)
is a point on the curve. The curve is sometimes called X0(n), though often that is used for the abstract algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
for which there exist various models. A related object is the classical modular polynomial, a polynomial in one variable defined as Φn(x, x).
Geometry of the modular curve
Parametrization of the modular curve
When n = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 16, 18, or 25, X0(n) has genusGeometric genus
In algebraic geometry, the geometric genus is a basic birational invariant pg of algebraic varieties and complex manifolds.-Definition:...
zero, and hence can be parametrized by rational functions. The simplest nontrivial example is X0(2), where if
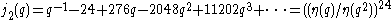
is (up to the constant term) the McKay–Thompson series for the class 2B of the Monster
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
, and η is the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
, then
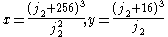
parametrizes X0(2) in terms of rational functions of j2. It is not necessary to actually compute j2 to use this parametrization; it can be taken as an arbitrary parameter.
Mappings
A curve C over the rationals Q such that there exists a surjective morphism from X0(n) to C for some n, given by a rational map with integer coefficients- φ:X0(n) → C,
is a modular curve
Modular curve
In number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
. The famous modularity theorem tells us that all elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s over Q are modular.
Mappings also arise in connection with X0(n) since points on it correspond to n-isogenous pairs of elliptic curves. Two elliptic curves are isogenous if there is a morphism of varieties (defined by a rational map) between the curves which is also a group homomorphism, respecting the group law on the elliptic curves, and hence which sends the point at infinity (serving as the identity of the group law) to the point at infinity. The isogenies with cyclic kernel of degree n, the cyclic isogenies, correspond to points on X0(n).
When X0(n) has genus one, it will itself be isomorphic to an elliptic curve, which will have the same j-invariant
J-invariant
In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
. For instance, X0(11) has j-invariant -122023936/161051 = - 21211-5313, and is isomorphic to the curve y2+y = x3-x2-10x-20. If we substitute this value of j for y in X0(5), we obtain two rational roots and a factor of degree four. The two rational roots correspond to isomorphism classes of curves with rational coefficients which are 5-isogenous to the above curve, but not isomorphic, having a different function field.
Specifically, we have the six rational points x=-122023936/161051, y=-4096/11, x=-122023936/161051, y=-52893159101157376/11, and x=-4096/11, y=-52893159101157376/11, plus the three points exchanging x and y, all on X0(5), corresponding to the six isogenies between these three curves. If in the curve y2+y = x3-x2-10x-20 isomorphic to X0(11) we substitute
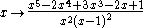
and
and factor, we get an extraneous factor of a rational function of x, and the curve y^2+y=x^3-x^2, with j-invariant -4096/11. Hence both curves are modular of level 11, having mappings from X0(11).
By a theorem of Henri Carayol, if an elliptic curve E is modular then its conductor, an isogeny invariant described originally in terms of cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
,
is the smallest integer n such that there exists a rational mapping φ:X0(n) → E. Since we now know all elliptic curves over Q are modular, we also know that the conductor is simply the level n of its minimal modular parametrization.
Galois theory of the modular curve
The Galois theory of the modular curve was investigated by Erich HeckeErich Hecke
Erich Hecke was a German mathematician. He obtained his doctorate in Göttingen under the supervision of David Hilbert. Kurt Reidemeister and Heinrich Behnke were among his students....
. Considered as a polynomial in x with coefficients in Z[y], the modular equation Φ0(n) is a polynomial of degree ψ(n) in x, whose roots generate a Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
of Q(y). In the case of X0(p) with p prime, where the characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of the field is not p, the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of
- Q(x, y)/Q(y)
is PGL2(p), the projective general linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
of linear fractional transformations of the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
of the field of p elements, which has p+1 points, the degree of X0(p).
This extension contains an algebraic extension
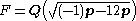
of Q. If we extend the field of constants to be F, we now have an extension with Galois group PSL2(p), the projective special linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
of the field with p elements, which is a finite simple group. By specializing y to a specific field element, we can, outside of a thin set, obtain an infinity of examples of fields with Galois group PSL2(p) over F, and PGL2(p) over Q.
When n is not a prime, the Galois groups can be analyzed in terms of the factors of n as a wreath product
Wreath product
In mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
.
External links
- Sequence in the OEIS: Genus of X0(n)
- http://www.math.uwaterloo.ca/~mrubinst/modularpolynomials/phi_l.html Coefficients of X0(n)