Classification of Clifford algebras
Encyclopedia
In abstract algebra
, in particular in the theory of nondegenerate
quadratic form
s on vector space
s, the structures of finite-dimensional real
and complex
Clifford algebra
s have been completely classified. In each case, the Clifford algebra is algebra isomorphic
to a full matrix ring
over R, C, or H (the quaternion
s), or to a direct sum of two such algebras, though not in a canonical
way. Below it is shown that distinct Clifford algebras may be algebra isomorphic, as is the case of Cℓ2,0(R) and Cℓ1,1(R) which are both isomorphic to the ring of two-by-two matrices over the real numbers.
s in this article are with respect to this ring product. Other products defined within Clifford algebras, such as the exterior product, are not used here.
This article uses the (+) sign convention
for Clifford multiplication so that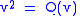
for all vectors , where Q is the quadratic form on the vector space V. We will denote the algebra of matrices
with entries in the division algebra
K by K(n). The direct sum of algebras will be denoted by .
and stable orthogonal group
, and is called Bott periodicity. The connection is explained by the geometric model of loop spaces approach to Bott periodicity: there 2-fold/8-fold periodic embeddings of the classical group
s in each other (corresponding to isomorphism groups of Clifford algebras), and their successive quotients are symmetric space
s which are homotopy equivalent to the loop spaces of the unitary/orthogonal group.
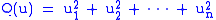
where n = dim V, so there is essentially only one Clifford algebra in each dimension. We will denote the Clifford algebra on Cn with the standard quadratic form by Cℓn(C).
There are two separate cases to consider, according to whether n is even or odd. When n is even the algebra Cℓn(C) is central simple
and so by the Artin-Wedderburn theorem is isomorphic to a matrix algebra over C. When n is odd, the center includes not only the scalars but the pseudoscalars (degree n elements) as well. We can always find a normalized pseudoscalar ω such that ω2 = 1. Define the operators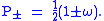
These two operators form a complete set of orthogonal idempotents, and since they are central they give a decomposition of Cℓn(C) into a direct sum of two algebras
where 
.
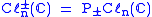The algebras Cℓn±(C) are just the positive and negative eigenspaces of ω and the P± are just the projection operators. Since ω is odd these algebras are mixed by α (the linear map on V defined by ):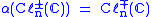
.
and therefore isomorphic (since α is an automorphism
). These two isomorphic algebras are each central simple and so, again, isomorphic to a matrix algebra over C. The sizes of the matrices can be determined from the fact that the dimension of Cℓn(C) is 2n. What we have then is the following table:
The even subalgebra of Cℓn(C) is (non-canonically) isomorphic to Cℓn−1(C). When n is even, the even subalgebra can be identified with the block diagonal matrices (when partitioned into 2×2 block matrix
). When n is odd, the even subalgebra are those elements of for which the two factors are identical. Picking either piece then gives an isomorphism with .
Every nondegenerate quadratic form on a real vector space is equivalent to the standard diagonal form: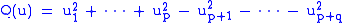
where is the dimension of the vector space. The pair of integers (p, q) is called the signature
of the quadratic form. The real vector space with this quadratic form is often denoted Rp,q. The Clifford algebra on Rp,q is denoted Cℓp,q(R).
A standard orthonormal basis
{ei} for Rp,q consists of mutually orthogonal vectors, p of which have norm +1 and q of which have norm −1.
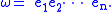
This is both a Coxeter element of sorts (product of reflections) and a longest element of a Coxeter group
in the Bruhat order
; this is an analogy. It corresponds to and generalizes a volume form
(in the exterior algebra
; for the trivial quadratic form, the unit pseudoscalar is a volume form), and lifts reflection through the origin (meaning that the image of the unit pseudoscalar is reflection through the origin, in the orthogonal group
).
To compute the square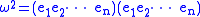
,
one can either reverse the order of the second group,
yielding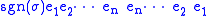
,
or apply a perfect shuffle,
yielding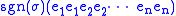
.
These both have sign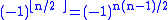
, which is 4-periodic (proof), and combined with 
, this shows that the square of ω is given by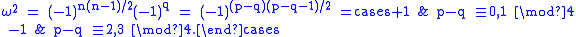
Note that, unlike the complex case, it is not always possible to find a pseudoscalar which squares to +1.
and so isomorphic to a matrix algebra over R or H by the Artin-Wedderburn theorem.
If n (equivalently) is odd then the algebra is no longer central simple but rather has a center which includes the pseudoscalars as well as the scalars. If n is odd and (equivalently, if )
then, just as in the complex case, the algebra Cℓp,q(R) decomposes into a direct sum of isomorphic algebras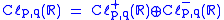
each of which is central simple and so isomorphic to matrix algebra over R or H.
If n is odd and ω2 = −1 (equivalently, if ) then the center of Cℓp,q(R) is isomorphic to C and can be consider as a complex algebra. As a complex algebra, it is central simple and so isomorphic to a matrix algebra over C.
Each of these properties depends only on the signature modulo
8. The complete classification table is given below. The size of the matrices is determined by the requirement that Cℓp,q(R) have dimension 2p+q.
It may be seen that of all matrix ring types mentioned, there is only one type shared between both complex and real algebras: the type C(2m). For example, Cℓ2(C) and Cℓ3,0(R) are both determined to be C(2). It is important to note that there is a difference in the classifying isomorphisms used. Since the Cℓ2(C) is algebra isomorphic via a C-linear map (which is necessarily R-linear), and Cℓ3,0(R) is algebra isomorphic via an R-linear map, Cℓ2(C) and Cℓ3,0(R) are R-algebra isomorphic.
A table of this classification for follows. Here runs vertically and runs horizontally (e.g. the algebra is found in row 4, column −2).
Write for matrices with coefficients in A, and for the real Clifford algebra.
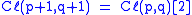
(Going over 4 spots in any row yields an identical algebra.)
From these Bott periodicity follows:
If the signature satisfies then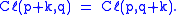
(The table is symmetric about columns with signature 1, 5, −3, −7, and so forth.)
Thus if the signature satisfies ,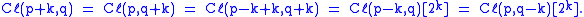
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, in particular in the theory of nondegenerate
Degeneracy (mathematics)
In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....
quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s on vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, the structures of finite-dimensional real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s have been completely classified. In each case, the Clifford algebra is algebra isomorphic
Algebra homomorphism
A homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
to a full matrix ring
Matrix ring
In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
over R, C, or H (the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s), or to a direct sum of two such algebras, though not in a canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
way. Below it is shown that distinct Clifford algebras may be algebra isomorphic, as is the case of Cℓ2,0(R) and Cℓ1,1(R) which are both isomorphic to the ring of two-by-two matrices over the real numbers.
Notation and conventions
The Clifford product is the manifest ring product for the Clifford algebra, and all algebra homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s in this article are with respect to this ring product. Other products defined within Clifford algebras, such as the exterior product, are not used here.
This article uses the (+) sign convention
Sign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
for Clifford multiplication so that
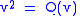
for all vectors , where Q is the quadratic form on the vector space V. We will denote the algebra of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with entries in the division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
K by K(n). The direct sum of algebras will be denoted by .
Bott periodicity
Clifford algebras exhibit a 2-fold periodicity over the complex numbers and an 8-fold periodicity over the real numbers, which is related to the same periodicities for homotopy groups of the stable unitary groupUnitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
and stable orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
, and is called Bott periodicity. The connection is explained by the geometric model of loop spaces approach to Bott periodicity: there 2-fold/8-fold periodic embeddings of the classical group
Classical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
s in each other (corresponding to isomorphism groups of Clifford algebras), and their successive quotients are symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
s which are homotopy equivalent to the loop spaces of the unitary/orthogonal group.
Complex case
The complex case is particularly simple: every nondegenerate quadratic form on a complex vector space is equivalent to the standard diagonal form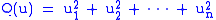where n = dim V, so there is essentially only one Clifford algebra in each dimension. We will denote the Clifford algebra on Cn with the standard quadratic form by Cℓn(C).
There are two separate cases to consider, according to whether n is even or odd. When n is even the algebra Cℓn(C) is central simple
Central simple algebra
In ring theory and related areas of mathematics a central simple algebra over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K...
and so by the Artin-Wedderburn theorem is isomorphic to a matrix algebra over C. When n is odd, the center includes not only the scalars but the pseudoscalars (degree n elements) as well. We can always find a normalized pseudoscalar ω such that ω2 = 1. Define the operators
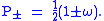
These two operators form a complete set of orthogonal idempotents, and since they are central they give a decomposition of Cℓn(C) into a direct sum of two algebras
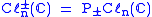where .The algebras Cℓn±(C) are just the positive and negative eigenspaces of ω and the P± are just the projection operators. Since ω is odd these algebras are mixed by α (the linear map on V defined by ):
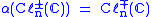.and therefore isomorphic (since α is an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
). These two isomorphic algebras are each central simple and so, again, isomorphic to a matrix algebra over C. The sizes of the matrices can be determined from the fact that the dimension of Cℓn(C) is 2n. What we have then is the following table:
| n | Cℓn(C) |
| 2m | C(2m) |
| 2m+1 | C(2m) ⊕ C(2m) |
The even subalgebra of Cℓn(C) is (non-canonically) isomorphic to Cℓn−1(C). When n is even, the even subalgebra can be identified with the block diagonal matrices (when partitioned into 2×2 block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
). When n is odd, the even subalgebra are those elements of for which the two factors are identical. Picking either piece then gives an isomorphism with .
Real case
The real case is significantly more complicated, exhibiting a periodicity of 8 rather than 2, and there is a 2-parameter family of Clifford algebras.Classification of quadratic form
Firstly, there are non-isomorphic quadratic forms of a given degree, classified by signature.Every nondegenerate quadratic form on a real vector space is equivalent to the standard diagonal form:
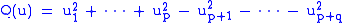
where is the dimension of the vector space. The pair of integers (p, q) is called the signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
of the quadratic form. The real vector space with this quadratic form is often denoted Rp,q. The Clifford algebra on Rp,q is denoted Cℓp,q(R).
A standard orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
{ei} for Rp,q consists of mutually orthogonal vectors, p of which have norm +1 and q of which have norm −1.
Unit pseudoscalar
The unit pseudoscalar in Cℓp,q(R) is defined as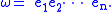This is both a Coxeter element of sorts (product of reflections) and a longest element of a Coxeter group
Longest element of a Coxeter group
In mathematics, the longest element of a Coxeter group is the unique element of maximal length in a finite Coxeter group with respect to the chosen generating set consisting of simple reflections. It is often denoted by w0...
in the Bruhat order
Bruhat order
In mathematics, the Bruhat order is a partial order on the elements of a Coxeter group, that corresponds to the inclusion order on Schubert varieties.-History:The Bruhat order on the Schubert varieties of a flag manifold or Grassmannian...
; this is an analogy. It corresponds to and generalizes a volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
(in the exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
; for the trivial quadratic form, the unit pseudoscalar is a volume form), and lifts reflection through the origin (meaning that the image of the unit pseudoscalar is reflection through the origin, in the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
).
To compute the square
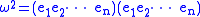,one can either reverse the order of the second group,
yielding
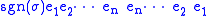,or apply a perfect shuffle,
yielding
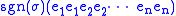.These both have sign
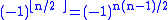, which is 4-periodic (proof), and combined with , this shows that the square of ω is given by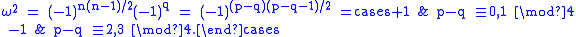Note that, unlike the complex case, it is not always possible to find a pseudoscalar which squares to +1.
Center
If n (equivalently) is even the algebra Cℓp,q(R) is central simpleCentral simple algebra
In ring theory and related areas of mathematics a central simple algebra over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K...
and so isomorphic to a matrix algebra over R or H by the Artin-Wedderburn theorem.
If n (equivalently) is odd then the algebra is no longer central simple but rather has a center which includes the pseudoscalars as well as the scalars. If n is odd and (equivalently, if )
then, just as in the complex case, the algebra Cℓp,q(R) decomposes into a direct sum of isomorphic algebras
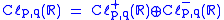
each of which is central simple and so isomorphic to matrix algebra over R or H.
If n is odd and ω2 = −1 (equivalently, if ) then the center of Cℓp,q(R) is isomorphic to C and can be consider as a complex algebra. As a complex algebra, it is central simple and so isomorphic to a matrix algebra over C.
Classification
All told there are three properties which determine the class of the algebra Cℓp,q(R):- signature mod 2: n is even/odd: central simple or not
- signature mod 4: ω2 = ±1: if not central simple, center is or C
- signature mod 8: the Brauer classBrauer groupIn mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is...
of the algebra (n even) or even subalgebra (n odd) is R or H
Each of these properties depends only on the signature modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
8. The complete classification table is given below. The size of the matrices is determined by the requirement that Cℓp,q(R) have dimension 2p+q.
| p−q mod 8 | ω2 | Cℓp,q(R) (n = p+q) |
p−q mod 8 | ω2 | Cℓp,q(R) (n = p+q) |
| 0 | + | R(2n/2) | 1 | + | R(2(n−1)/2)⊕R(2(n−1)/2) |
| 2 | − | R(2n/2) | 3 | − | C(2(n−1)/2) |
| 4 | + | H(2(n−2)/2) | 5 | + | H(2(n−3)/2)⊕H(2(n−3)/2) |
| 6 | − | H(2(n−2)/2) | 7 | − | C(2(n−1)/2) |
It may be seen that of all matrix ring types mentioned, there is only one type shared between both complex and real algebras: the type C(2m). For example, Cℓ2(C) and Cℓ3,0(R) are both determined to be C(2). It is important to note that there is a difference in the classifying isomorphisms used. Since the Cℓ2(C) is algebra isomorphic via a C-linear map (which is necessarily R-linear), and Cℓ3,0(R) is algebra isomorphic via an R-linear map, Cℓ2(C) and Cℓ3,0(R) are R-algebra isomorphic.
A table of this classification for follows. Here runs vertically and runs horizontally (e.g. the algebra is found in row 4, column −2).
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | −1 | −2 | −3 | −4 | −5 | −6 | −7 | −8 | |
| 0 | R | ||||||||||||||||
| 1 | R2 | C | |||||||||||||||
| 2 | R(2) | R(2) | H | ||||||||||||||
| 3 | C(2) | R2(2) | C(2) | H2 | |||||||||||||
| 4 | H(2) | R(4) | R(4) | H(2) | H(2) | ||||||||||||
| 5 | H2(2) | C(4) | R2(4) | C(4) | H2(2) | C(4) | |||||||||||
| 6 | H(4) | H(4) | R(8) | R(8) | H(4) | H(4) | R(8) | ||||||||||
| 7 | C(8) | H2(4) | C(8) | R2(8) | C(8) | H2(4) | C(8) | R2(8) | |||||||||
| 8 | R(16) | H(8) | H(8) | R(16) | R(16) | H(8) | H(8) | R(16) | R(16) | ||||||||
| ω2 | + | − | − | + | + | − | − | + | + | − | − | + | + | − | − | + | + |
Symmetries
There is a tangled web of symmetries and relationships in the above table.Write for matrices with coefficients in A, and for the real Clifford algebra.
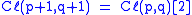
(Going over 4 spots in any row yields an identical algebra.)
From these Bott periodicity follows:
If the signature satisfies then
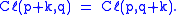
(The table is symmetric about columns with signature 1, 5, −3, −7, and so forth.)
Thus if the signature satisfies ,
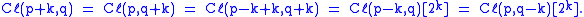
See also
- Dirac algebraDirac algebraIn mathematical physics, the Dirac algebra is the Clifford algebra Cℓ1,3 which is generated by matrix multiplication and real and complex linear combination over the Dirac gamma matrices, introduced by the mathematical physicist P. A. M...
Cℓ1,3(C) - Pauli algebra Cℓ3,0(C)
- Spacetime algebraSpacetime algebraIn mathematical physics, spacetime algebra is a name for the Clifford algebra Cℓ1,3,or Geometric algebra G4 = G which can be particularly closely associated with the geometry of special relativity and relativistic spacetime....
- Clifford module
- Spin representation