Clustering coefficient
Encyclopedia
In graph theory
, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties (Holland and Leinhardt, 1971; Watts and Strogatz, 1998). In real-world networks, this likelihood tends to be greater than the average probability of a tie randomly established between two nodes (Holland and Leinhardt, 1971; Watts and Strogatz, 1998).
Two versions of this measure exist: the global and the local. The global version was designed to give an overall indication of the clustering in the network, whereas the local gives an indication of the embeddedness of single nodes.
Formally, it has been defined as:
A generalisation to weighted networks was proposed by Opsahl and Panzarasa (2009), and a redefinition to two-mode networks (both binary and weighted) by Opsahl (2009).
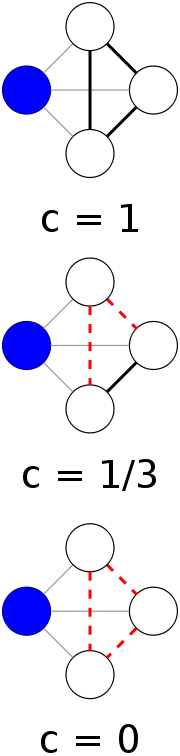The local clustering coefficient of a vertex
in a graph
quantifies how close its neighbors
are to being a clique
(complete graph). Duncan J. Watts
and Steven Strogatz
introduced the measure in 1998 to determine whether a graph is a small-world network
.
A graph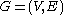
formally consists of a set of vertices 
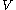and a set of edges 
between them. An edge 
connects vertex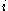 
with vertex 
.
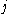The neighbourhood
N for a vertex
is defined as its immediately connected neighbours as follows:
We define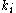
as the number of vertices, 
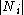, in the neighbourhood, 
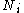, of a vertex.
The local clustering coefficient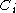
for a vertex 
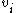is then given by the proportion of links between the vertices within its neighbourhood divided by the number of links that could possibly exist between them. For a directed graph, 
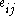is distinct from 
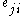, and therefore for each neighbourhood 
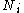there are 
links that could exist among the vertices within the neighbourhood (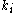
is the total (in + out) degree of the vertex). Thus, the local clustering coefficient for directed graphs is given as
An undirected graph has the property that
and 
are considered identical. Therefore, if a vertex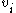 
has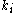 
neighbours, 
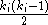edges could exist among the vertices within the neighbourhood. Thus, the local clustering coefficient for undirected graphs can be defined as
Let
be the number of triangles on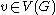 
for undirected graph 
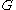. That is, 
is the number of subgraphs of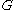 
with 3 edges and 3 vertices, one of which is 
. Let 
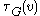be the number of triples on 
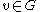. That is, 
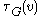is the number of subgraphs (not necessarily induced) with 2 edges and 3 vertices, one of which is 
and such that 
is incident to both edges. Then we can also define the clustering coefficient as
It is simple to show that the two preceding definitions are the same, since
These measures are 1 if every neighbour connected to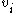
is also connected to every other vertex within the neighbourhood, and 0 if no vertex that is connected to 
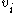connects to any other vertex that is connected to 
.
:
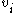A graph is considered small-world
, if its average clustering coefficient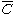
is significantly higher than a random graph
constructed on the same vertex set, and if the graph has approximately the same mean-shortest path length
as its corresponding random graph
.
A generalisation to weighted networks was proposed by Barrat et al. (2004), and a redefinition to bipartite graph
s (also called two-mode networks) by Latapy et al. (2008)
and Opsahl (2009).
This formula is not, by default, defined for graphs with isolated vertices; see Kaiser, (2008) and Barmpoutis et al.
The networks with the largest possible average clustering coefficient are found to have a modular structure, and at the same time, they have the smallest possible average distance among the different nodes.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties (Holland and Leinhardt, 1971; Watts and Strogatz, 1998). In real-world networks, this likelihood tends to be greater than the average probability of a tie randomly established between two nodes (Holland and Leinhardt, 1971; Watts and Strogatz, 1998).
Two versions of this measure exist: the global and the local. The global version was designed to give an overall indication of the clustering in the network, whereas the local gives an indication of the embeddedness of single nodes.
Global clustering coefficient
The global clustering coefficient is based on triplets of nodes. A triplet consists of three nodes that are connected by either two (open triplet) or three (closed triplet) undirected ties. A triangle consists of three closed triplets, one centred on each of the nodes. The global clustering coefficient is the number of closed triplets (or 3 x triangles) over the total number of triplets (both open and closed). The first attempt to measure it was made by Luce and Perry (1949). This measure gives an indication of the clustering in the whole network (global), and can be applied to both undirected and directed networks (often called transitivity, see Wasserman and Faust, 1994, page 243).Formally, it has been defined as:
A generalisation to weighted networks was proposed by Opsahl and Panzarasa (2009), and a redefinition to two-mode networks (both binary and weighted) by Opsahl (2009).
Local clustering coefficient
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
in a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
quantifies how close its neighbors
Neighbourhood (graph theory)
In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the induced subgraph of G consisting of all vertices adjacent to v and all edges connecting two such vertices. For example, the image shows a...
are to being a clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
(complete graph). Duncan J. Watts
Duncan J. Watts
Duncan J. Watts is an Australian researcher and a principal research scientist at Yahoo! Research, where he directs the Human Social Dynamics group. He is also a past external faculty member of the Santa Fe Institute and a former professor of sociology at Columbia University, where he headed the...
and Steven Strogatz
Steven Strogatz
Steven Henry Strogatz is an American mathematician and the Jacob Gould Schurman Professor of Applied Mathematics at Cornell University...
introduced the measure in 1998 to determine whether a graph is a small-world network
Small-world network
In mathematics, physics and sociology, a small-world network is a type of mathematical graph in which most nodes are not neighbors of one another, but most nodes can be reached from every other by a small number of hops or steps...
.
A graph
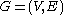formally consists of a set of vertices 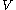and a set of edges between them. An edge connects vertex 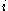with vertex 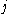.The neighbourhood
Neighbourhood (graph theory)
In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the induced subgraph of G consisting of all vertices adjacent to v and all edges connecting two such vertices. For example, the image shows a...
N for a vertex
is defined as its immediately connected neighbours as follows:
We define
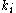as the number of vertices, 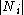, in the neighbourhood, 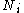, of a vertex.The local clustering coefficient
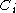for a vertex 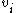is then given by the proportion of links between the vertices within its neighbourhood divided by the number of links that could possibly exist between them. For a directed graph, 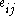is distinct from 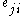, and therefore for each neighbourhood 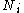there are links that could exist among the vertices within the neighbourhood (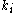 is the total (in + out) degree of the vertex). Thus, the local clustering coefficient for directed graphs is given as
An undirected graph has the property that
and are considered identical. Therefore, if a vertex 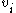has 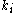neighbours, 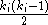edges could exist among the vertices within the neighbourhood. Thus, the local clustering coefficient for undirected graphs can be defined as
Let
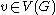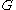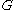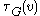be the number of triangles on for undirected graph . That is, is the number of subgraphs of with 3 edges and 3 vertices, one of which is . Let be the number of triples on 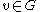. That is, 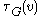is the number of subgraphs (not necessarily induced) with 2 edges and 3 vertices, one of which is and such that is incident to both edges. Then we can also define the clustering coefficient as
It is simple to show that the two preceding definitions are the same, since
These measures are 1 if every neighbour connected to
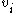is also connected to every other vertex within the neighbourhood, and 0 if no vertex that is connected to 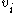connects to any other vertex that is connected to 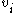.Network average clustering coefficient
The clustering coefficient for the whole network is given by Watts and Strogatz as the average of the local clustering coefficients of all the vertices :
A graph is considered small-world
Small-world network
In mathematics, physics and sociology, a small-world network is a type of mathematical graph in which most nodes are not neighbors of one another, but most nodes can be reached from every other by a small number of hops or steps...
, if its average clustering coefficient
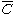is significantly higher than a random graphRandom graph
In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
constructed on the same vertex set, and if the graph has approximately the same mean-shortest path length
Distance (graph theory)
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...
as its corresponding random graph
Random graph
In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
.
A generalisation to weighted networks was proposed by Barrat et al. (2004), and a redefinition to bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
s (also called two-mode networks) by Latapy et al. (2008)
and Opsahl (2009).
This formula is not, by default, defined for graphs with isolated vertices; see Kaiser, (2008) and Barmpoutis et al.
The networks with the largest possible average clustering coefficient are found to have a modular structure, and at the same time, they have the smallest possible average distance among the different nodes.