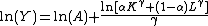Cobb-Douglas
Encyclopedia
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, the Cobb–Douglas functional form of production function
Production function
In microeconomics and macroeconomics, a production function is a function that specifies the output of a firm, an industry, or an entire economy for all combinations of inputs...
s is widely used to represent the relationship of an output to inputs. Similar functions were originally used by Knut Wicksell
Knut Wicksell
Johan Gustaf Knut Wicksell was a leading Swedish economist of the Stockholm school. His economic contributions would influence both the Keynesian and Austrian schools of economic thought....
(1851–1926), while the Cobb-Douglas form was developed and tested against statistical evidence by Charles Cobb
Charles Cobb (economist)
Charles Wiggins Cobb was an American mathematician and economist. He published many works on both subjects, however he is most famous for developing the Cobb–Douglas formula in economics. He worked on this project with the economist Paul Douglas while lecturing at the Amherst College in...
and Paul Douglas
Paul Douglas
Paul Howard Douglas was an liberal American politician and University of Chicago economist. A war hero, he was elected as a Democratic U.S. Senator from Illinois from in the 1948 landslide, serving until his defeat in 1966...
during 1900–1947.
Formulation
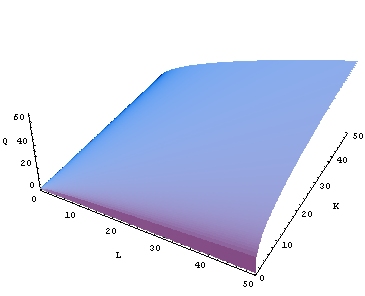
In its most standard form for production of a single good with two factors, the function is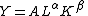
where:
- Y = total production (the monetary value of all goods produced in a year)
- L = labor input
- K = capitalCapital (economics)In economics, capital, capital goods, or real capital refers to already-produced durable goods used in production of goods or services. The capital goods are not significantly consumed, though they may depreciate in the production process...
input - A = total factor productivityTotal factor productivityIn economics, total-factor productivity is a variable which accounts for effects in total output not caused by inputs. If all inputs are accounted for, then total factor productivity can be taken as a measure of an economy’s long-term technological change or technological dynamism.If all inputs...
- α and β are the output elasticitiesOutput elasticityIn economics, output elasticity is the percentage change of output divided by the percentage change of an input. It is sometimes called partial output elasticity to clarify that it refers to the change of only one input....
of labor and capital, respectively. These values are constants determined by available technology.
Output elasticity measures the responsiveness of output to a change in levels of either labor or capital used in production, ceteris paribus
Ceteris paribus
or is a Latin phrase, literally translated as "with other things the same," or "all other things being equal or held constant." It is an example of an ablative absolute and is commonly rendered in English as "all other things being equal." A prediction, or a statement about causal or logical...
. For example if α = 0.15, a 1% increase in labor would lead to approximately a 0.15% increase in output.
Further, if:
- α + β = 1,
the production function has constant returns to scale: Doubling capital K and labour L will also double output Y. If
- α + β < 1,
returns to scale are decreasing, and if
- α + β > 1
returns to scale are increasing. Assuming perfect competition
Perfect competition
In economic theory, perfect competition describes markets such that no participants are large enough to have the market power to set the price of a homogeneous product. Because the conditions for perfect competition are strict, there are few if any perfectly competitive markets...
and α + β = 1, α and β can be shown to be labor and capital's share of output.
Cobb and Douglas were influenced by statistical evidence that appeared to show that labor and capital shares of total output were constant over time in developed countries; they explained this by statistical fitting least-squares regression
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
of their production function. There is now doubt over whether constancy over time exists.
History
Paul DouglasPaul Douglas
Paul Howard Douglas was an liberal American politician and University of Chicago economist. A war hero, he was elected as a Democratic U.S. Senator from Illinois from in the 1948 landslide, serving until his defeat in 1966...
explains that his first formulation of the Cobb–Douglas production function was developed in 1927, when seeking a functional form to relate estimates he had calculated for workers and capital, he spoke with mathematician and colleague Charles Cobb
Charles Cobb (economist)
Charles Wiggins Cobb was an American mathematician and economist. He published many works on both subjects, however he is most famous for developing the Cobb–Douglas formula in economics. He worked on this project with the economist Paul Douglas while lecturing at the Amherst College in...
who suggested a function of the form
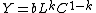 previously used by Knut Wicksell
previously used by Knut WicksellKnut Wicksell
Johan Gustaf Knut Wicksell was a leading Swedish economist of the Stockholm school. His economic contributions would influence both the Keynesian and Austrian schools of economic thought....
. Estimating this using least squares
Ordinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
, he obtained a result for the marginal productivity of labour (k) to 0.75$ --- which was subsequently confirmed by the National Bureau of Economic Research
National Bureau of Economic Research
The National Bureau of Economic Research is an American private nonprofit research organization "committed to undertaking and disseminating unbiased economic research among public policymakers, business professionals, and the academic community." The NBER is well known for providing start and end...
to be %74.1. Later work in the 1940s prompted them to allow for the exponents on C and L vary, resulting in estimates that subsequently proved to be very close to improved measure of productivity developed at that time.
A major criticism at the time was that estimates of the production function, although seemingly accurate, were based on such sparse data that it was hard to give them much credibility. Douglas' remarked "I must admit I was discouraged by this criticism and thought of giving up the effort, but there was something which told me I should hold on." The breakthrough came in using US census data, which was cross sectional and provided a large number of observations. Douglas presented the results of these findings, along with those for other countries, at his 1947 address as president of the American Economic Association
American Economic Association
The American Economic Association, or AEA, is a learned society in the field of economics, headquartered in Nashville, Tennessee. It publishes one of the most prestigious academic journals in economics: the American Economic Review...
. Shortly afterwards, Douglas went into politics and was stricken by ill health --- resulting in little further development on his side. However, two decades later, his production function was widely used, being adopted by economists such as Paul Samuelson
Paul Samuelson
Paul Anthony Samuelson was an American economist, and the first American to win the Nobel Memorial Prize in Economic Sciences. The Swedish Royal Academies stated, when awarding the prize, that he "has done more than any other contemporary economist to raise the level of scientific analysis in...
and Solow. The Cobb–Douglas production function is especially notable for being the first time an aggregate or economy-wide production function had been developed, estimated, and the presented to the profession for analysis; it marked a landmark change in how economists approached macroeconomics
Macroeconomics
Macroeconomics is a branch of economics dealing with the performance, structure, behavior, and decision-making of the whole economy. This includes a national, regional, or global economy...
.
Dimensional analysis
The Cobb–Douglas model is criticized by some AustrianAustrian School
The Austrian School of economics is a heterodox school of economic thought. It advocates methodological individualism in interpreting economic developments , the theory that money is non-neutral, the theory that the capital structure of economies consists of heterogeneous goods that have...
economists such as William Barnett II on the basis of dimensional analysis
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
. They argue it does not having meaningful or economically reasonable units of measurement
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
unless
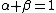 . However, other economists in reply to Barnett have argued that the units used are not fundamentally more unnatural than other units commonly used in physics such a log
. However, other economists in reply to Barnett have argued that the units used are not fundamentally more unnatural than other units commonly used in physics such a logLogarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
temperature or distance squared.
Lack of microfoundations
The Cobb–Douglas production function was not developed on the basis of any knowledge of engineering, technology, or management of the production process. It was instead developed because it had attractive mathematical characteristics, such as diminishing marginal returnsDiminishing returns
In economics, diminishing returns is the decrease in the marginal output of a production process as the amount of a single factor of production is increased, while the amounts of all other factors of production stay constant.The law of diminishing returns In economics, diminishing returns (also...
to either factor of production and the property that expenditure on any given input is a constant fraction of total cost. Crucially, there are no microfoundations
Microfoundations
In economics, the term microfoundations refers to the microeconomic analysis of the behavior of individual agents such as households or firms that underpins a macroeconomic theory....
for it. In the modern era, economists try to build models up from individual agents acting, rather than imposing a functional form on an entire economy. However, many modern authors have developed models which give Cobb–Douglas production function from the micro level; many New Keynesian models, for example. It is nevertheless a mathematical mistake to assume that just because the Cobb–Douglas function applies at the micro-level, it also always applies at the macro-level. Similarly, it is not necessarily the case that a macro Cobb–Douglas applies at the disaggregated level. An early microfoundation of the aggregate Cobb–Douglas technology based on linear activities is derived in Houthakker (1955).
Some applications
Nonetheless, the Cobb–Douglas function has been applied to many other contexts besides production. It can be applied to utilityUtility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
as follows:
U(x1,x2)=x1αx2β;
where x1 and x2 are the quantities consumed of good #1 and good #2.
In its generalized form, where x1, x2, ... ,xL are the quantities consumed of good #1, good #2, ..., good #L, a utility function representing the Cobb–Douglas preferences may be written as:
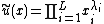
with x = (x1, x2, ... ,xL). Setting
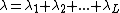 and because the function
and because the function 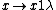
is strictly monotone for x > 0, it follows that
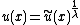 represents the same preferences. Setting
represents the same preferences. Setting 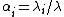 it can be shown that
it can be shown that 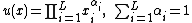
The utility may be maximized by looking at the logarithm of the utility
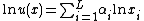
which makes the consumer's optimization problem:
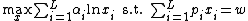
This has the solution that:
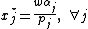
which has the interpretation that the per-unit fraction of the consumers incomes used in purchasing good j is exactly the marginal term
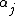
Various representations of the production function
The Cobb–Douglas function form can be estimated as a linear relationship using the following expression: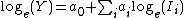
Where:
- Y = Output
- Ii = Inputs
- ai = model coefficients
The model can also be written as
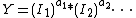
As noted, the common Cobb–Douglas function used in macroeconomic modeling is
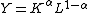
where K is capital and L is labor. When the model coefficients sum to one, as in this example, the production function is first-order homogeneous
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
, which implies constant returns to scale, that is, if all inputs are scaled by a common factor greater than zero, output will be scaled by the same factor.
Translog (transcendental logarithmic) production function
The translog production function is a generalization of the Cobb–Douglas production function. The name translog stands for 'transcendental logarithmic'.The three factor translog production function is:
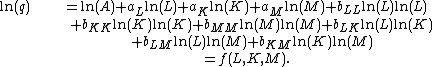
where L = labor, K = capital, M = materials and supplies, and q = product.
Derived from a CES function
Constant elasticity of substitutionConstant Elasticity of Substitution
In economics, Constant elasticity of substitution is a property of some production functions and utility functions.More precisely, it refers to a particular type of aggregator function which combines two or more types of consumption, or two or more types of productive inputs into an aggregate...
(CES) function:
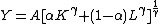
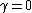 corresponds to a Cobb–Douglas function,
corresponds to a Cobb–Douglas function, 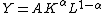
Proof:
Apply l'Hôpital's rule
L'Hôpital's rule
In calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
:
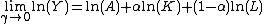
Therefore,
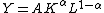
See also
- Production theory basicsProduction theory basicsProduction refers to the economic process of converting of inputs into outputs. Production uses resources to create a good or service that is suitable for use, gift-giving in a gift economy, or exchange in a market economy. This can include manufacturing, storing, shipping, and packaging. Some...
- Production, costs, and pricingProduction, costs, and pricingThe following outline is provided as an overview of and topical guide to industrial organization:Industrial organization – describes the behavior of firms in the marketplace with regard to production, pricing, employment and other decisions...
- Production possibility frontierProduction possibility frontierIn economics, a production–possibility frontier , sometimes called a production–possibility curve or product transformation curve, is a graph that compares the production rates of two commodities that use the same fixed total of the factors of production...
- MicroeconomicsMicroeconomicsMicroeconomics is a branch of economics that studies the behavior of how the individual modern household and firms make decisions to allocate limited resources. Typically, it applies to markets where goods or services are being bought and sold...
- Constant elasticity of substitutionConstant Elasticity of SubstitutionIn economics, Constant elasticity of substitution is a property of some production functions and utility functions.More precisely, it refers to a particular type of aggregator function which combines two or more types of consumption, or two or more types of productive inputs into an aggregate...