Constant Elasticity of Substitution
Encyclopedia
In economics
, Constant elasticity of substitution (CES) is a property of some production function
s and utility functions.
More precisely, it refers to a particular type of aggregator function which combines two or more types of consumption, or two or more types of productive inputs into an aggregate quantity. This aggregator function exhibits constant elasticity of substitution
.
is a type of production function that displays constant elasticity of substitution
. In other words, the production technology has a constant percentage change in factor (e.g. labour
and capital
) proportions due to a percentage change in marginal rate of technical substitution. The two factor (Capital, Labor) CES production function introduced by Solow
and later made popular by Arrow
, Chenery
, Minhas
, and Solow
is:
where
As its name suggests, the CES production function exhibits constant elasticity of substitution between capital and labor.
Leontief
, linear and Cobb-Douglas
production functions are special cases of the CES production function. That is, in the limit as
approaches 1, we get the Cobb-Douglas function; as 
approaches positive infinity we get the linear (perfect substitutes) function; and for 
approaching 0, we get the Leontief (perfect complements) function. The general form of the CES production function is:
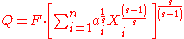
where
Extending the CES (Solow) form to accommodate multiple factors of production creates some problems, however. There is no completely general way to do this. Uzawa showed the only possible n-factor production functions (n>2) with constant partial elasticities of substitution require either that all elasticities between pairs of factors be identical, or if any differ, these all must equal each other and all remaining elasticities must be unity. This is true for any production function. This means the use of the CES form for more than 2 factors will generally mean that there is not constant elasticity of substitution among all factors.
Nested CES functions are commonly found in partial/general equilibrium models. Different nests (levels) allow for the introduction of the appropriate elasticity of substitution.
The CES is a neoclassical production function.
. For example, if there exist
types of consumption goods 
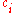, then aggregate consumption 
could be defined using the CES aggregator:
Here again, the coefficients
are share parameters, and 
is the elasticity of substitution. Therefore the consumption goods 
are perfect substitutes when 
approaches infinity and perfect complements when 
approaches zero. The CES aggregator is also sometimes called the Armington aggregator, which was discussed by Armington (1969).
A CES utility function is one of the cases considered by Avinash Dixit
and Joseph Stiglitz in their study of optimal product diversity in a context of monopolistic competition
.
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, Constant elasticity of substitution (CES) is a property of some production function
Production function
In microeconomics and macroeconomics, a production function is a function that specifies the output of a firm, an industry, or an entire economy for all combinations of inputs...
s and utility functions.
More precisely, it refers to a particular type of aggregator function which combines two or more types of consumption, or two or more types of productive inputs into an aggregate quantity. This aggregator function exhibits constant elasticity of substitution
Elasticity of substitution
Elasticity of substitution is the elasticity of the ratio of two inputs to a production function with respect to the ratio of their marginal products . It measures the curvature of an isoquant and thus, the substitutability between inputs , i.e...
.
CES production function
The CES production functionProduction function
In microeconomics and macroeconomics, a production function is a function that specifies the output of a firm, an industry, or an entire economy for all combinations of inputs...
is a type of production function that displays constant elasticity of substitution
Elasticity of substitution
Elasticity of substitution is the elasticity of the ratio of two inputs to a production function with respect to the ratio of their marginal products . It measures the curvature of an isoquant and thus, the substitutability between inputs , i.e...
. In other words, the production technology has a constant percentage change in factor (e.g. labour
Manual labour
Manual labour , manual or manual work is physical work done by people, most especially in contrast to that done by machines, and also to that done by working animals...
and capital
Capital (economics)
In economics, capital, capital goods, or real capital refers to already-produced durable goods used in production of goods or services. The capital goods are not significantly consumed, though they may depreciate in the production process...
) proportions due to a percentage change in marginal rate of technical substitution. The two factor (Capital, Labor) CES production function introduced by Solow
Robert Solow
Robert Merton Solow is an American economist particularly known for his work on the theory of economic growth that culminated in the exogenous growth model named after him...
and later made popular by Arrow
Kenneth Arrow
Kenneth Joseph Arrow is an American economist and joint winner of the Nobel Memorial Prize in Economics with John Hicks in 1972. To date, he is the youngest person to have received this award, at 51....
, Chenery
Hollis B. Chenery
Hollis Burnley Chenery was an American economist well known for his pioneering contribution in the field of development economics.-Early life:...
, Minhas
Bagicha Singh Minhas
Padma Bhushan Dr. Bagicha Singh Minhas was an eminent Indian economist.-Education:Dr. Minhas was born in Punjab and obtained his first degree of BSc from Khalsa College, Amritsar, and a Master’s degree in economics from Punjab University...
, and Solow
Robert Solow
Robert Merton Solow is an American economist particularly known for his work on the theory of economic growth that culminated in the exogenous growth model named after him...
is:
where
-
= Output -
= Factor productivity -
= Share parameter -
, 
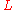= Primary production factors (Capital and Labor) -
= 
-
= 
= Elasticity of substitution.
As its name suggests, the CES production function exhibits constant elasticity of substitution between capital and labor.
Leontief
Leontief production function
In economics, the Leontief production function or fixed proportions production function is a production function that implies the factors of production will be used in fixed proportions, as there is no substitutability between factors...
, linear and Cobb-Douglas
Cobb-Douglas
In economics, the Cobb–Douglas functional form of production functions is widely used to represent the relationship of an output to inputs. Similar functions were originally used by Knut Wicksell , while the Cobb-Douglas form was developed and tested against statistical evidence by Charles Cobb and...
production functions are special cases of the CES production function. That is, in the limit as
approaches 1, we get the Cobb-Douglas function; as approaches positive infinity we get the linear (perfect substitutes) function; and for approaching 0, we get the Leontief (perfect complements) function. The general form of the CES production function is: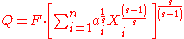where
-
= Output -
= Factor productivity -
= Share parameter -
= Production factors (i = 1,2...n) -
= Elasticity of substitution.
Extending the CES (Solow) form to accommodate multiple factors of production creates some problems, however. There is no completely general way to do this. Uzawa showed the only possible n-factor production functions (n>2) with constant partial elasticities of substitution require either that all elasticities between pairs of factors be identical, or if any differ, these all must equal each other and all remaining elasticities must be unity. This is true for any production function. This means the use of the CES form for more than 2 factors will generally mean that there is not constant elasticity of substitution among all factors.
Nested CES functions are commonly found in partial/general equilibrium models. Different nests (levels) allow for the introduction of the appropriate elasticity of substitution.
The CES is a neoclassical production function.
CES utility function
The same functional form arises as a utility function in consumer theoryConsumer theory
Consumer choice is a theory of microeconomics that relates preferences for consumption goods and services to consumption expenditures and ultimately to consumer demand curves. The link between personal preferences, consumption, and the demand curve is one of the most closely studied relations in...
. For example, if there exist
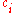types of consumption goods , then aggregate consumption could be defined using the CES aggregator:Here again, the coefficients
are share parameters, and is the elasticity of substitution. Therefore the consumption goods are perfect substitutes when approaches infinity and perfect complements when approaches zero. The CES aggregator is also sometimes called the Armington aggregator, which was discussed by Armington (1969).A CES utility function is one of the cases considered by Avinash Dixit
Avinash Dixit
Avinash Kamalakar Dixit is an Indian-American economist originally of Indian nationality.-Education:Dixit received a B.Sc. from Bombay University in 1963 in Mathematics and Physics, a B.A...
and Joseph Stiglitz in their study of optimal product diversity in a context of monopolistic competition
Monopolistic competition
Monopolistic competition is imperfect competition where many competing producers sell products that are differentiated from one another...
.