Code (set theory)
Encyclopedia
In set theory
, a code for a hereditarily countable set
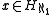
is a set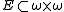
such that there is an isomorphism
between (ω,E) and (X,
) where X is the transitive closure
of {x}. If X is finite (with cardinality n), then use n×n instead of ω×ω and (n,E) instead of (ω,E).
According to the axiom of extensionality
, the identity of a set is determined by its elements. And since those elements are also sets, their identities are determined by their elements, etc.. So if one knows the element relation restricted to X, then one knows what x is. (We use the transitive closure of {x} rather than of x itself to avoid confusing the elements of x with elements of its elements or whatever.) A code includes that information identifying x and also information about the particular injection from X into ω which was used to create E. The extra information about the injection is non-essential, so there are many codes for the same set which are equally useful.
So codes are a way of mapping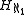
into the powerset of ω×ω. Using a pairing function
on ω (such as (n,k) goes to (n2+2·n·k+k2+n+3·k)/2), we can map the powerset of ω×ω into the powerset of ω. And we can map the powerset of ω into the Cantor set
, a subset of the real number
s. So statements about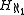
can be converted into statements about the reals. Consequently,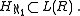 
Codes are useful in constructing mice
.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a code for a hereditarily countable set
Hereditarily countable set
In set theory, a set is called hereditarily countable if it is a countable set of hereditarily countable sets. This inductive definition is in fact well-founded and can be expressed in the language of first-order set theory. A set is hereditarily countable if and only if it is countable, and every...
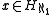
is a set
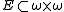
such that there is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
between (ω,E) and (X,
) where X is the transitive closureTransitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
of {x}. If X is finite (with cardinality n), then use n×n instead of ω×ω and (n,E) instead of (ω,E).
According to the axiom of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
, the identity of a set is determined by its elements. And since those elements are also sets, their identities are determined by their elements, etc.. So if one knows the element relation restricted to X, then one knows what x is. (We use the transitive closure of {x} rather than of x itself to avoid confusing the elements of x with elements of its elements or whatever.) A code includes that information identifying x and also information about the particular injection from X into ω which was used to create E. The extra information about the injection is non-essential, so there are many codes for the same set which are equally useful.
So codes are a way of mapping
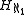into the powerset of ω×ω. Using a pairing functionPairing function
In mathematics a pairing function is a process to uniquely encode two natural numbers into a single natural number.Any pairing function can be used in set theory to prove that integers and rational numbers have the same cardinality as natural numbers...
on ω (such as (n,k) goes to (n2+2·n·k+k2+n+3·k)/2), we can map the powerset of ω×ω into the powerset of ω. And we can map the powerset of ω into the Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
, a subset of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. So statements about
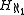can be converted into statements about the reals. Consequently,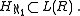 Codes are useful in constructing mice
Mouse (set theory)
In set theory, a mouse is a small model of Zermelo-Fraenkel set theory with desirable properties. The exact definition depends on the context. In most cases, there is a technical definition of "premouse" and an added condition of iterability : a mouse is then an iterable premouse...
.