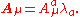
Color charge
Encyclopedia
In particle physics
, color charge is a property of quark
s and gluon
s that is related to the particles' strong interaction
s in the theory of quantum chromodynamics
(QCD). Color charge has analogies with the notion of electric charge
of particles, but because of the mathematical complications of QCD, there are many technical differences. The "color" of quarks and gluons is completely unrelated to visual perception of color
. Rather, it is a name for a property that has almost no manifestation at distances above the size of an atomic nucleus
. The term color was chosen because the abstract property to which it refers has three aspects, which are analogized to the three primary color
s of red, green, and blue. By comparison, the electromagnetic charge has a single aspect, which takes the values positive or negative.
Shortly after the existence of quarks was first proposed in 1964, Oscar W. Greenberg
introduced the notion of color charge to explain how quarks could coexist inside some hadron
s in otherwise identical quantum states without violating the Pauli exclusion principle
. The theory of quantum chromodynamics has been under development since the 1970s and constitutes an important component of the Standard Model
of particle physics.
The following illustrates the coupling constant
s for color-charged particles:
, a coupling constant
and a charge are different but related notions. The coupling constant sets the magnitude of the force of interaction; for example, in quantum electrodynamics
, the fine-structure constant
is a coupling constant. The charge in a gauge theory
has to do with the way a particle transforms under the gauge symmetry; i.e., its representation
under the gauge group. For example, the electron
has charge -1 and the positron
has charge +1, implying that the gauge transformation has opposite effects on them in some sense. Specifically, if a local gauge transformation φ(x) is applied in electrodynamics, then one finds
where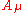
is the photon
field, and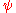
is the electron field with 
(a bar over 
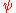denotes its antiparticle — the positron). Since QCD is a non-abelian
theory, the representations, and hence the color charges, are more complicated. They are dealt with in the next section.
(3) and contains a triplet of fields together denoted by ψ. The antiquark field belongs to the complex conjugate representation
(3*) and also contains a triplet of fields. We can write
The gluon contains an octet of fields, belongs to the adjoint representation
(8), and can be written using the Gell-Mann matrices
as
All other particle
s belong to the trivial representation
(1) of color SU(3). The color charge of each of these fields is fully specified by the representations. Quarks have a color charge of red, green or blue and antiquarks have a color charge of antired, antigreen or antiblue. Gluons have a combination of two color charges (one of red, green or blue and one of antired, antigreen and antiblue) in a superposition of states which are given by the Gell-Mann matrices
. All other particles have zero color charge. Mathematically speaking, the color charge of a particle is the value of a certain quadratic Casimir operator in the representation of the particle.
In the simple language introduced previously, the three indices "1", "2" and "3" in the quark triplet above are usually identified with the three colors. The colorful language misses the following point. A gauge transformation in color SU(3) can be written as ψ → Uψ, where U is a 3X3 matrix which belongs to the group SU(3). Thus, after gauge transformation, the new colors are linear combinations of the old colors. In short, the simplified language introduced before is not gauge invariant.
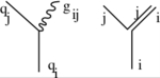
Color charge is conserved, but the book-keeping involved in this is more complicated than just adding up the charges, as is done in quantum electrodynamics. One simple way of doing this is to look at the interaction vertex in QCD and replace it by a color line representation. The meaning is the following. Let ψi represent the i-th component of a quark field (loosely called the i-th color). The color of a gluon is similarly given by a which corresponds to the particular Gell-Mann matrix it is associated with. This matrix has indices i and j. These are the color labels on the gluon. At the interaction vertex one has qi→gij+qj. The color-line representation tracks these indices. Color charge conservation means that the ends of these color-lines must be either in the initial or final state, equivalently, that no lines break in the middle of a diagram.
Since gluons carry color charge, two gluons can also interact. A typical interaction vertex (called the three gluon vertex) for gluons involves g+g→g. This is shown here, along with its color line representation. The color-line diagrams can be restated in terms of conservation laws of color; however, as noted before, this is not a gauge invariant language. Note that in a typical non-Abelian gauge theory the gauge boson
carries the charge of the theory, and hence has interactions of this kind; for example, the W boson in the electroweak theory. In the electroweak theory, the W also carries electric charge, and hence interacts with a photon.
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, color charge is a property of quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s and gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s that is related to the particles' strong interaction
Strong interaction
In particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
s in the theory of quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
(QCD). Color charge has analogies with the notion of electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
of particles, but because of the mathematical complications of QCD, there are many technical differences. The "color" of quarks and gluons is completely unrelated to visual perception of color
Color
Color or colour is the visual perceptual property corresponding in humans to the categories called red, green, blue and others. Color derives from the spectrum of light interacting in the eye with the spectral sensitivities of the light receptors...
. Rather, it is a name for a property that has almost no manifestation at distances above the size of an atomic nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
. The term color was chosen because the abstract property to which it refers has three aspects, which are analogized to the three primary color
Primary color
Primary colors are sets of colors that can be combined to make a useful range of colors. For human applications, three primary colors are usually used, since human color vision is trichromatic....
s of red, green, and blue. By comparison, the electromagnetic charge has a single aspect, which takes the values positive or negative.
Shortly after the existence of quarks was first proposed in 1964, Oscar W. Greenberg
Oscar W. Greenberg
Oscar Wallace Greenberg is an American physicist and professor at University of Maryland, College Park. He is famous for positing the existence of a property of subatomic particles called color charge.-Educational background:...
introduced the notion of color charge to explain how quarks could coexist inside some hadron
Hadron
In particle physics, a hadron is a composite particle made of quarks held together by the strong force...
s in otherwise identical quantum states without violating the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
. The theory of quantum chromodynamics has been under development since the 1970s and constitutes an important component of the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics.
Red, green, and blue
In QCD, a quark's color can take one of three values, called red, green, and blue. An antiquark can take one of three anticolors, called antired, antigreen, and antiblue (represented as cyan, magenta and yellow, respectively). Gluons are mixtures of two colors, such as red and antigreen, which constitutes their color charge. QCD considers eight gluons of the possible nine color-anticolor combinations to be unique; see eight gluon colors for an explanation.The following illustrates the coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
s for color-charged particles:
Coupling constant and charge
In a quantum field theoryQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, a coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
and a charge are different but related notions. The coupling constant sets the magnitude of the force of interaction; for example, in quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, the fine-structure constant
Fine-structure constant
In physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
is a coupling constant. The charge in a gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
has to do with the way a particle transforms under the gauge symmetry; i.e., its representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
under the gauge group. For example, the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
has charge -1 and the positron
Positron
The positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
has charge +1, implying that the gauge transformation has opposite effects on them in some sense. Specifically, if a local gauge transformation φ(x) is applied in electrodynamics, then one finds
-
, 
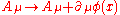and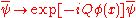 
where
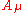is the photonPhoton
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
field, and
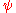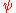is the electron field with (a bar over denotes its antiparticle — the positron). Since QCD is a non-abelianNonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
theory, the representations, and hence the color charges, are more complicated. They are dealt with in the next section.
Quark and gluon fields and color charges
In QCD the gauge group is the non-Abelian group SU(3). The running coupling is usually denoted by αs. Each flavor of quark belongs to the fundamental representationFundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
(3) and contains a triplet of fields together denoted by ψ. The antiquark field belongs to the complex conjugate representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
(3*) and also contains a triplet of fields. We can write
-
and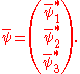 
The gluon contains an octet of fields, belongs to the adjoint representation
Adjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
(8), and can be written using the Gell-Mann matrices
Gell-Mann matrices
The Gell-Mann matrices, named for Murray Gell-Mann, are one possible representation of the infinitesimal generators of the special unitary group called SU....
as
All other particle
Subatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
s belong to the trivial representation
Trivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
(1) of color SU(3). The color charge of each of these fields is fully specified by the representations. Quarks have a color charge of red, green or blue and antiquarks have a color charge of antired, antigreen or antiblue. Gluons have a combination of two color charges (one of red, green or blue and one of antired, antigreen and antiblue) in a superposition of states which are given by the Gell-Mann matrices
Gell-Mann matrices
The Gell-Mann matrices, named for Murray Gell-Mann, are one possible representation of the infinitesimal generators of the special unitary group called SU....
. All other particles have zero color charge. Mathematically speaking, the color charge of a particle is the value of a certain quadratic Casimir operator in the representation of the particle.
In the simple language introduced previously, the three indices "1", "2" and "3" in the quark triplet above are usually identified with the three colors. The colorful language misses the following point. A gauge transformation in color SU(3) can be written as ψ → Uψ, where U is a 3X3 matrix which belongs to the group SU(3). Thus, after gauge transformation, the new colors are linear combinations of the old colors. In short, the simplified language introduced before is not gauge invariant.
Gauge boson
In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
carries the charge of the theory, and hence has interactions of this kind; for example, the W boson in the electroweak theory. In the electroweak theory, the W also carries electric charge, and hence interacts with a photon.