Compact quantum group
Encyclopedia
In mathematics
, a compact quantum group is an abstract structure on a unital separable C*-algebra axiomatized from those that exist on the commutative C*-algebra of "continuous complex-valued functions" on a compact quantum group.
The basic motivation for this theory comes from the following analogy. The space of complex-valued functions on a compact Hausdorff topological space forms a commutative C*-algebra. On the other hand, by the Gelfand Theorem
, a commutative C*-algebra is isomorphic to the C*-algebra of continuous complex-valued functions on a compact Hausdorff topological space, and the topological space is uniquely determined by the C*-algebra up to homeomorphism
.
S. L. Woronowicz
introduced the important concept of compact matrix quantum groups, which he initially called compact pseudogroups. Compact matrix quantum groups are abstract structures on which the "continuous functions" on the structure are given by elements of a C*-algebra. The geometry of a compact matrix quantum group is a special case of a noncommutative geometry
.
,
, there exists a C*-algebra homomorphism
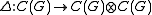
where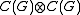
is the minimal C*-algebra tensor product — the completion of the algebraic tensor product
of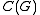
and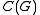 
) — such that
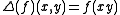
for all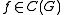
, and for all 
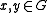, where
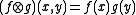
for all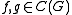
and all 
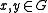. There also exists a linear multiplicative mapping
,
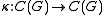such that
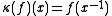
for all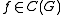
and all 
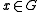. Strictly speaking, this does not make 
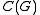into a Hopf algebra
, unless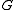
is finite.
On the other hand, a finite-dimensional representation
of G can be used to generate a *-subalgebra of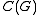
which is also a Hopf *-algebra. Specifically, if
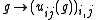
is an
-dimensional representation
of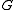
, then
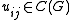
for all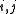
, and
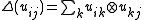
for all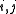
. It follows that the *-algebra generated by 
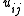for all 
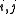and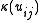 
for all 
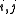is a Hopf *-algebra: the counit is determined by
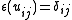
for all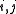
(where 
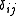is the Kronecker delta), the antipode is 
, and the unit is given by
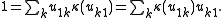
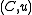, where 
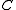is a C*-algebra and
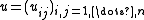
is a matrix with entries in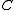
such that
As a consequence of continuity, the comultiplication on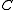
is coassociative.
In general,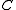
is a bialgebra, and 
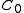is a Hopf *-algebra.
Informally,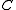
can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and 
can be regarded as a finite-dimensional representation of the compact matrix quantum group.
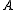and 
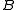acting on the Hilbert spaces 
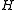and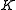 
respectively, their minimal tensor product is defined to be the norm completion of the algebraic tensor product 
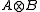in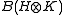 
; the norm completion is also denoted by 
.
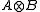A compact quantum group is defined as a pair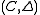
, where 
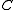is a unital separable C*-algebra and
of the Hopf *-algebra (a corepresentation of a counital coassiative coalgebra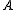
is a square matrix
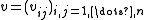
with entries in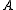
(so 
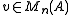) such that
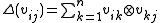
for all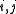
and
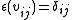for all 
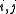). Furthermore, a representation, v, is called unitary if the matrix for v is unitary, or equivalently, if
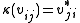for all i, j.
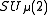
, where the parameter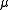
is a positive real number. So 
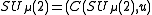, where 
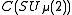is the C*-algebra generated by 
and 
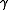,subject to
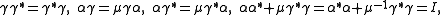
and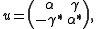
so that the comultiplication is determined by 
, 
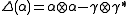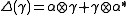, and the coinverse is determined by 
, 
, 
, 
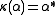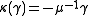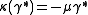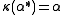. Note that 
is a representation, but not a unitary representation
.
is equivalent to the unitary representation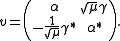 
Equivalently,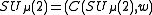
, where 
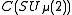is the C*-algebra generated by 
and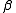 
,subject to
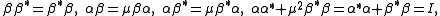
and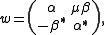
so that the comultiplication is determined by 
, 
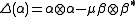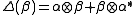, and the coinverse is determined by 
, 
, 
, 
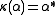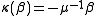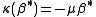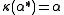. Note that 
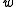is a unitary representation. The realizations can be identified by equating 
.
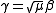When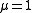
, then 
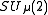is equal to the concrete compact group 
.
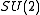Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a compact quantum group is an abstract structure on a unital separable C*-algebra axiomatized from those that exist on the commutative C*-algebra of "continuous complex-valued functions" on a compact quantum group.
The basic motivation for this theory comes from the following analogy. The space of complex-valued functions on a compact Hausdorff topological space forms a commutative C*-algebra. On the other hand, by the Gelfand Theorem
Gelfand representation
In mathematics, the Gelfand representation in functional analysis has two related meanings:* a way of representing commutative Banach algebras as algebras of continuous functions;...
, a commutative C*-algebra is isomorphic to the C*-algebra of continuous complex-valued functions on a compact Hausdorff topological space, and the topological space is uniquely determined by the C*-algebra up to homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
.
S. L. Woronowicz
S. L. Woronowicz
Stanisław Lech Woronowicz is a Polish mathematician and physicist.It was Woronowicz, and Erling Størmer, who classified positive maps in the low dimensional cases. This translates to the Peres-Horodecki criterion, in the context of quantum information theory. He is also known for contributions to...
introduced the important concept of compact matrix quantum groups, which he initially called compact pseudogroups. Compact matrix quantum groups are abstract structures on which the "continuous functions" on the structure are given by elements of a C*-algebra. The geometry of a compact matrix quantum group is a special case of a noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
.
Formulation
For a compact topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
,
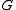, there exists a C*-algebra homomorphism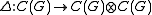where
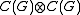is the minimal C*-algebra tensor product — the completion of the algebraic tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of
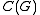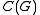and ) — such that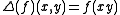for all
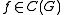, and for all 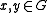, where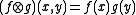for all
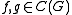and all 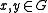. There also exists a linear multiplicative mapping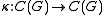,such that
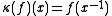
for all
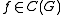and all 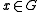. Strictly speaking, this does not make 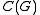into a Hopf algebraHopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
, unless
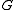is finite.On the other hand, a finite-dimensional representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of G can be used to generate a *-subalgebra of
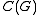which is also a Hopf *-algebra. Specifically, if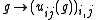is an
-dimensional representationRepresentation
Representation can refer to:* Representation , one's ability to influence the political process* Representative democracy* Representation, a type of diplomatic mission...
of
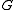, then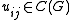for all
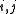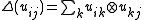
, andfor all
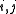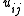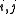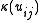. It follows that the *-algebra generated by for all and for all 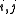is a Hopf *-algebra: the counit is determined by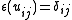for all
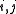(where 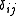is the Kronecker delta), the antipode is , and the unit is given by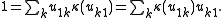Compact Matrix Quantum Groups
As a generalization, a compact matrix quantum group is defined as a pair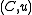, where 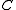is a C*-algebra and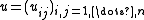is a matrix with entries in
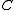such that- The *-subalgebra,
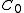, of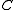 
, which is generated by the matrix elements of 
, is dense in 
;
- There exists a C*-algebra homomorphism
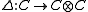(where 
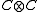is the C*-algebra tensor product - the completion of the algebraic tensor product of 
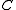and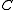 
) such that 
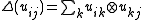for all 
(
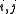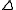is called the comultiplication);
- There exists a linear antimultiplicative map
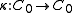(the coinverse) such that 
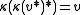for all 
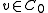and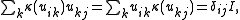 
where 
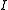is the identity element of 
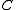. Since 
is antimultiplicative, then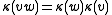 
for all 
.
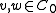As a consequence of continuity, the comultiplication on
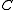is coassociative.In general,
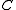is a bialgebra, and 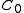is a Hopf *-algebra.Informally,
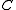can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and can be regarded as a finite-dimensional representation of the compact matrix quantum group.Compact Quantum Groups
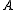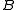For C*-algebras and acting on the Hilbert spaces 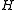and 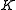respectively, their minimal tensor product is defined to be the norm completion of the algebraic tensor product 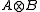in 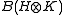; the norm completion is also denoted by 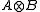.A compact quantum group is defined as a pair
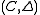, where 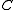is a unital separable C*-algebra and
-
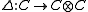is a C*-algebra unital homomorphism satisfying 
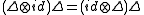; such that
- the sets
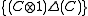and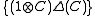 
are dense in 
.
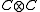Representations
A representation of the compact matrix quantum group is given by a corepresentationCoalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
of the Hopf *-algebra (a corepresentation of a counital coassiative coalgebra
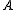is a square matrix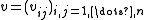with entries in
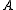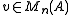(so ) such that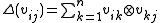for all
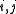and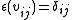 for all 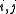). Furthermore, a representation, v, is called unitary if the matrix for v is unitary, or equivalently, if 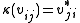for all i, j.Example
An example of a compact matrix quantum group is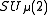, where the parameter
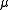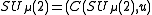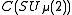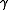is a positive real number. So , where is the C*-algebra generated by and ,subject to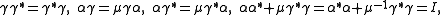and
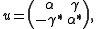so that the comultiplication is determined by 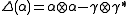, , 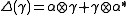and the coinverse is determined by 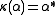, , 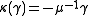, 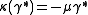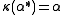. Note that is a representation, but not a unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
.
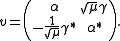
is equivalent to the unitary representation Equivalently,
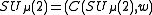, where 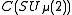is the C*-algebra generated by and 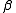,subject to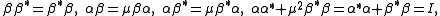and
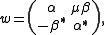so that the comultiplication is determined by 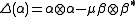, , 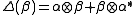and the coinverse is determined by 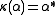, , 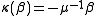, 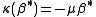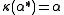. Note that 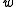is a unitary representation. The realizations can be identified by equating 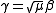.When
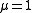, then 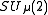is equal to the concrete compact group .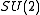