
Companion matrix
Encyclopedia
In linear algebra
, the companion matrix of the monic polynomial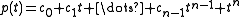
is the square matrix defined as

With this convention, and writing the basis
as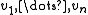 , one has
, one has 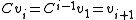 (for
(for 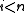 ), and
), and 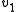 generates V as a
generates V as a 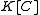 -module: C cycles basis vectors.
-module: C cycles basis vectors.
Some authors use the transpose
of this matrix, which (dually) cycles coordinates, and is more convenient for some purposes, like linear recursive relations.
as well as the minimal polynomial
of C(p) are equal to p;
in this sense, the matrix C(p) is the "companion" of the polynomial p.
If A is an n-by-n matrix with entries from some field
K, then the following statements are equivalent:
Not every square matrix is similar to a companion matrix. But every matrix is similar to a matrix made up of blocks of companion matrices. Furthermore, these companion matrices can be chosen so that their polynomials divide each other; then they are uniquely determined by A. This is the rational canonical form
of A.
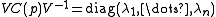
where V is the Vandermonde matrix corresponding to the λ's.
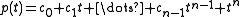
the (transpose) companion matrix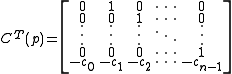
generates the sequence, in the sense that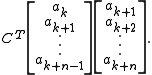
It increments the series by 1.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the companion matrix of the monic polynomial
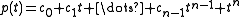
is the square matrix defined as

With this convention, and writing the basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
as
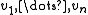 , one has
, one has 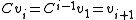 (for
(for 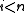 ), and
), and 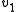 generates V as a
generates V as a 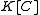 -module: C cycles basis vectors.
-module: C cycles basis vectors.Some authors use the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of this matrix, which (dually) cycles coordinates, and is more convenient for some purposes, like linear recursive relations.
Characterization
The characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
as well as the minimal polynomial
Minimal polynomial (linear algebra)
In linear algebra, the minimal polynomial of an n-by-n matrix A over a field F is the monic polynomial P over F of least degree such that P=0...
of C(p) are equal to p;
in this sense, the matrix C(p) is the "companion" of the polynomial p.
If A is an n-by-n matrix with entries from some field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, then the following statements are equivalent:
- A is similar to the companion matrix over K of its characteristic polynomial
- the characteristic polynomial of A coincides with the minimal polynomial of A, equivalently the minimal polynomial has degree n
- there exists a cyclic vector v in
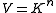 for A, meaning that {v, Av, A2v,...,An-1v} is a basisBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for A, meaning that {v, Av, A2v,...,An-1v} is a basisBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of V. Equivalently, such that V is cyclic as a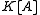 -module (and
-module (and 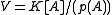 ); one says that A is regular.
); one says that A is regular.
Not every square matrix is similar to a companion matrix. But every matrix is similar to a matrix made up of blocks of companion matrices. Furthermore, these companion matrices can be chosen so that their polynomials divide each other; then they are uniquely determined by A. This is the rational canonical form
Frobenius normal form
In linear algebra, the Frobenius normal form, Turner binormal projective form or rational canonical form of a square matrix A is a canonical form for matrices that reflects the structure of the minimal polynomial of A and provides a means of detecting whether another matrix B is similar to A...
of A.
Diagonalizability
If p(t) has distinct roots λ1,...,λn (the eigenvalues of C(p)), then C(p) is diagonalizable as follows: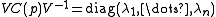
where V is the Vandermonde matrix corresponding to the λ's.
Linear recursive sequences
Given a linear recursive sequence with characteristic polynomial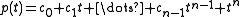
the (transpose) companion matrix
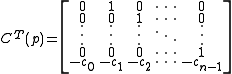
generates the sequence, in the sense that
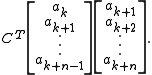
It increments the series by 1.

