Complete-linkage clustering
Encyclopedia
In cluster analysis, complete linkage or farthest neighbour is a method of calculating distances between clusters in agglomerative hierarchical clustering
. In complete linkage, the distance between two clusters is computed as the maximum distance between a pair of objects, one in one cluster, and one in the other.
As an agglomerative procedure, the clusters are initially the singletons (single-member clusters). At each stage the individuals or groups of individuals that are closest according to the linkage criterion are joined to form a new, larger cluster. At the last stage, a single group consisting of all individuals is formed.
Mathematically, the complete linkage function — the distance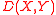
between clusters 
and 
— is described by the following expression :
where
Complete linkage clustering avoids a drawback of the alternative single linkage
method - the so-called chaining phenomenon, where clusters formed via single linkage clustering may be forced together due to single elements being close to each other, even though many of the elements in each cluster may be very distant to each other. Complete linkage tends to find compact clusters of approximately equal diameters.
scheme that erases rows and columns in a proximity matrix as old clusters are merged into new ones. The
proximity matrix D contains all distances d(i,j). The clusterings are assigned sequence numbers 0,1,......, (n − 1) and L(k) is the level of the kth clustering. A cluster with sequence number m is denoted (m) and the proximity between clusters (r) and (s) is denoted d[(r),(s)].
The algorithm is composed of the following steps:
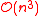. In 1977, D. Defays proposed an optimally efficient algorithm of only complexity 
known as CLINK inspired by the similar algorithm SLINK for single-linkage clustering.
and average linkage
clustering - implementing a different linkage in the naive algorithm is simply a matter of using a different formula to calculate inter-cluster distances in the initial computation of the proximity matrix and in step 4 of the above algorithm. An optimally efficient algorithm is however not available for arbitrary linkages. The formula that should be adjusted has been highlighted using bold text.
Hierarchical clustering
In statistics, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:...
. In complete linkage, the distance between two clusters is computed as the maximum distance between a pair of objects, one in one cluster, and one in the other.
As an agglomerative procedure, the clusters are initially the singletons (single-member clusters). At each stage the individuals or groups of individuals that are closest according to the linkage criterion are joined to form a new, larger cluster. At the last stage, a single group consisting of all individuals is formed.
Mathematically, the complete linkage function — the distance
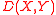between clusters and — is described by the following expression :where
-
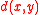is the distance between elements 
and 
; -
and 
are two sets of elements (clusters)
Complete linkage clustering avoids a drawback of the alternative single linkage
Single linkage clustering
In cluster analysis, single linkage, nearest neighbour or shortest distance is a method of calculating distances between clusters in hierarchical clustering...
method - the so-called chaining phenomenon, where clusters formed via single linkage clustering may be forced together due to single elements being close to each other, even though many of the elements in each cluster may be very distant to each other. Complete linkage tends to find compact clusters of approximately equal diameters.
Naive Algorithm
The following algorithm is an agglomerativeHierarchical clustering
In statistics, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:...
scheme that erases rows and columns in a proximity matrix as old clusters are merged into new ones. The
proximity matrix D contains all distances d(i,j). The clusterings are assigned sequence numbers 0,1,......, (n − 1) and L(k) is the level of the kth clustering. A cluster with sequence number m is denoted (m) and the proximity between clusters (r) and (s) is denoted d[(r),(s)].The algorithm is composed of the following steps:
- Begin with the disjoint clustering having level L(0) = 0 and sequence number m = 0.
- Find the most similar pair of clusters in the current clustering, say pair (r), (s), according to d[(r),(s)] = max d[(i),(j)] where the maximum is over all pairs of clusters in the current clustering.
- Increment the sequence number: m = m + 1. Merge clusters (r) and (s) into a single cluster to form the next clustering m. Set the level of this clustering to L(m) = d[(r),(s)]
- Update the proximity matrix, D, by deleting the rows and columns corresponding to clusters (r) and (s) and adding a row and column corresponding to the newly formed cluster. The proximity between the new cluster, denoted (r,s) and old cluster (k) is defined as d[(k), (r,s)] = max d[(k),(r)], d[(k),(s)].
- If all objects are in one cluster, stop. Else, go to step 2.
Optimally efficient algorithm
The algorithm explained above is easy to understand but of complexity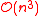. In 1977, D. Defays proposed an optimally efficient algorithm of only complexity known as CLINK inspired by the similar algorithm SLINK for single-linkage clustering.Other linkages
Alternative linkage schemes include single linkageSingle linkage clustering
In cluster analysis, single linkage, nearest neighbour or shortest distance is a method of calculating distances between clusters in hierarchical clustering...
and average linkage
UPGMA
UPGMA is a simple agglomerative or hierarchical clustering method used in bioinformatics for the creation of phenetic trees...
clustering - implementing a different linkage in the naive algorithm is simply a matter of using a different formula to calculate inter-cluster distances in the initial computation of the proximity matrix and in step 4 of the above algorithm. An optimally efficient algorithm is however not available for arbitrary linkages. The formula that should be adjusted has been highlighted using bold text.