
Hierarchical clustering
Encyclopedia
In statistics
, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy
of clusters. Strategies for hierarchical clustering generally fall into two types:
In general, the merges and splits are determined in a greedy
manner. The results of hierarchical clustering are usually presented in a dendrogram
.
In the general case, the complexity of agglomerative clustering is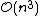 , which makes them too slow for large data sets. Divisive clustering with an exhaustive search is
, which makes them too slow for large data sets. Divisive clustering with an exhaustive search is 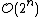 , which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity
, which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity 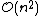 are known: SLINK for single-linkage and CLINK for complete-linkage clustering.
are known: SLINK for single-linkage and CLINK for complete-linkage clustering.
(a measure of distance
between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets.
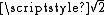 or 1 under Manhattan distance, Euclidean distance or maximum distance respectively.
or 1 under Manhattan distance, Euclidean distance or maximum distance respectively.
Some commonly used metrics for hierarchical clustering are:
|-
|}
For text or other non-numeric data, metrics such as the Hamming distance
or Levenshtein distance
are often used.
A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance.
Some commonly used linkage criteria between two sets of observations A and B are:
where d is the chosen metric. Other linkage criteria include:
is the distance metric
.
Cutting the tree at a given height will give a partitioning clustering at a selected precision. In this example, cutting after the second row will yield clusters {a} {b c} {d e} {f}. Cutting after the third row will yield clusters {a} {b c} {d e f}, which is a coarser clustering, with a smaller number of larger clusters.
The hierarchical clustering dendrogram
would be as such:
 This method builds the hierarchy from the individual elements by progressively merging clusters. In our example, we have six elements {a} {b} {c} {d} {e} and {f}. The first step is to determine which elements to merge in a cluster. Usually, we want to take the two closest elements, according to the chosen distance.
This method builds the hierarchy from the individual elements by progressively merging clusters. In our example, we have six elements {a} {b} {c} {d} {e} and {f}. The first step is to determine which elements to merge in a cluster. Usually, we want to take the two closest elements, according to the chosen distance.
Optionally, one can also construct a distance matrix
at this stage, where the number in the i-th row j-th column is the distance between the i-th and j-th elements. Then, as clustering progresses, rows and columns are merged as the clusters are merged and the distances updated. This is a common way to implement this type of clustering, and has the benefit of caching distances between clusters. A simple agglomerative clustering algorithm is described in the single-linkage clustering page; it can easily be adapted to different types of linkage (see below).
Suppose we have merged the two closest elements b and c, we now have the following clusters {a}, {b, c}, {d}, {e} and {f}, and want to merge them further. To do that, we need to take the distance between {a} and {b c}, and therefore define the distance between two clusters.
Usually the distance between two clusters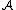 and
and 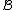 is one of the following:
is one of the following:
In statistics
, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy
of clusters. Strategies for hierarchical clustering generally fall into two types:
In general, the merges and splits are determined in a greedy
manner. The results of hierarchical clustering are usually presented in a dendrogram
.
In the general case, the complexity of agglomerative clustering is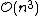 , which makes them too slow for large data sets. Divisive clustering with an exhaustive search is
, which makes them too slow for large data sets. Divisive clustering with an exhaustive search is 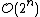 , which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity
, which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity 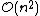 are known: SLINK for single-linkage and CLINK for complete-linkage clustering.
are known: SLINK for single-linkage and CLINK for complete-linkage clustering.
(a measure of distance
between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets.
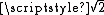 or 1 under Manhattan distance, Euclidean distance or maximum distance respectively.
or 1 under Manhattan distance, Euclidean distance or maximum distance respectively.
Some commonly used metrics for hierarchical clustering are:
|-
|}
For text or other non-numeric data, metrics such as the Hamming distance
or Levenshtein distance
are often used.
A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance.
Some commonly used linkage criteria between two sets of observations A and B are:
where d is the chosen metric. Other linkage criteria include:
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy
Hierarchy
A hierarchy is an arrangement of items in which the items are represented as being "above," "below," or "at the same level as" one another...
of clusters. Strategies for hierarchical clustering generally fall into two types:
- Agglomerative: This is a "bottom up" approach: each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy.
- Divisive: This is a "top down" approach: all observations start in one cluster, and splits are performed recursively as one moves down the hierarchy.
In general, the merges and splits are determined in a greedy
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
manner. The results of hierarchical clustering are usually presented in a dendrogram
Dendrogram
A dendrogram is a tree diagram frequently used to illustrate the arrangement of the clusters produced by hierarchical clustering...
.
In the general case, the complexity of agglomerative clustering is
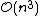 , which makes them too slow for large data sets. Divisive clustering with an exhaustive search is
, which makes them too slow for large data sets. Divisive clustering with an exhaustive search is 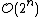 , which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity
, which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity 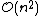 are known: SLINK for single-linkage and CLINK for complete-linkage clustering.
are known: SLINK for single-linkage and CLINK for complete-linkage clustering.Cluster dissimilarity
In order to decide which clusters should be combined (for agglomerative), or where a cluster should be split (for divisive), a measure of dissimilarity between sets of observations is required. In most methods of hierarchical clustering, this is achieved by use of an appropriate metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
(a measure of distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets.
Metric
The choice of an appropriate metric will influence the shape of the clusters, as some elements may be close to one another according to one distance and farther away according to another. For example, in a 2-dimensional space, the distance between the point (1,0) and the origin (0,0) is always 1 according to the usual norms, but the distance between the point (1,1) and the origin (0,0) can be 2,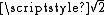 or 1 under Manhattan distance, Euclidean distance or maximum distance respectively.
or 1 under Manhattan distance, Euclidean distance or maximum distance respectively.Some commonly used metrics for hierarchical clustering are:
| Names | Formula |
|---|---|
| Euclidean distance Euclidean distance In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space... |
|
| squared Euclidean distance | |
| Manhattan distance | |
| maximum distance | |
| Mahalanobis distance Mahalanobis distance In statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936. It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown sample set to a known one. It differs from Euclidean... |
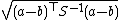 where S is the covariance matrix where S is the covariance matrixCovariance matrix In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector... |
| cosine similarity Cosine similarity Cosine similarity is a measure of similarity between two vectors by measuring the cosine of the angle between them. The cosine of 0 is 1, and less than 1 for any other angle. The cosine of the angle between two vectors thus determines whether two vectors are pointing in roughly the same... |
|-
|}
For text or other non-numeric data, metrics such as the Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
or Levenshtein distance
Levenshtein distance
In information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences...
are often used.
A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance.
Linkage criteria
The linkage criteria determines the distance between sets of observations as a function of the pairwise distances between observations.Some commonly used linkage criteria between two sets of observations A and B are:
| Names | Formula |
|---|---|
| Maximum or complete linkage clustering | 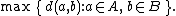 |
| Minimum or single-linkage clustering | 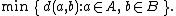 |
| Mean or average linkage clustering, or UPGMA UPGMA UPGMA is a simple agglomerative or hierarchical clustering method used in bioinformatics for the creation of phenetic trees... |
|
| Minimum energy clustering Energy distance Energy distance is a statistical distance between probability distributions. If X and Y are independent random vectors in Rd, with cumulative distribution functions F and G respectively, then the energy distance between the distributions F and G is definedwhere X, X' are independent and identically... |
where d is the chosen metric. Other linkage criteria include:
- The sum of all intra-cluster variance.
- The increase in variance for the cluster being merged ( Ward's criterion).
- The probability that candidate clusters spawn from the same distribution function (V-linkage).
Discussion
Hierarchical clustering has the distinct advantage that any valid measure of distance can be used. In fact, the observations themselves are not required: all that is used is a matrix of distances.Example for Agglomerative Clustering
For example, suppose this data is to be clustered, and the Euclidean distanceEuclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
is the distance metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
.
Cutting the tree at a given height will give a partitioning clustering at a selected precision. In this example, cutting after the second row will yield clusters {a} {b c} {d e} {f}. Cutting after the third row will yield clusters {a} {b c} {d e f}, which is a coarser clustering, with a smaller number of larger clusters.
The hierarchical clustering dendrogram
Dendrogram
A dendrogram is a tree diagram frequently used to illustrate the arrangement of the clusters produced by hierarchical clustering...
would be as such:

Optionally, one can also construct a distance matrix
Distance matrix
In mathematics, computer science and graph theory, a distance matrix is a matrix containing the distances, taken pairwise, of a set of points...
at this stage, where the number in the i-th row j-th column is the distance between the i-th and j-th elements. Then, as clustering progresses, rows and columns are merged as the clusters are merged and the distances updated. This is a common way to implement this type of clustering, and has the benefit of caching distances between clusters. A simple agglomerative clustering algorithm is described in the single-linkage clustering page; it can easily be adapted to different types of linkage (see below).
Suppose we have merged the two closest elements b and c, we now have the following clusters {a}, {b, c}, {d}, {e} and {f}, and want to merge them further. To do that, we need to take the distance between {a} and {b c}, and therefore define the distance between two clusters.
Usually the distance between two clusters
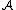 and
and 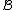 is one of the following:
is one of the following:
- The maximum distance between elements of each cluster (also called complete-linkage clusteringComplete-linkage clusteringIn cluster analysis, complete linkage or farthest neighbour is a method of calculating distances between clusters in agglomerative hierarchical clustering...
):
-
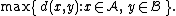
- The minimum distance between elements of each cluster (also called single-linkage clustering):
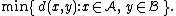
- The mean distance between elements of each cluster (also called average linkage clustering, used e.g. in UPGMAUPGMAUPGMA is a simple agglomerative or hierarchical clustering method used in bioinformatics for the creation of phenetic trees...
):
- The mean distance between elements of each cluster (also called average linkage clustering, used e.g. in UPGMA
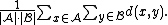
- The sum of all intra-cluster variance.
- The increase in variance for the cluster being merged ( Ward's method
In statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy
Hierarchy
A hierarchy is an arrangement of items in which the items are represented as being "above," "below," or "at the same level as" one another...
of clusters. Strategies for hierarchical clustering generally fall into two types:
- Agglomerative: This is a "bottom up" approach: each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy.
- Divisive: This is a "top down" approach: all observations start in one cluster, and splits are performed recursively as one moves down the hierarchy.
In general, the merges and splits are determined in a greedy
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
manner. The results of hierarchical clustering are usually presented in a dendrogram
Dendrogram
A dendrogram is a tree diagram frequently used to illustrate the arrangement of the clusters produced by hierarchical clustering...
.
In the general case, the complexity of agglomerative clustering is
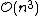 , which makes them too slow for large data sets. Divisive clustering with an exhaustive search is
, which makes them too slow for large data sets. Divisive clustering with an exhaustive search is 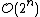 , which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity
, which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity 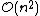 are known: SLINK for single-linkage and CLINK for complete-linkage clustering.
are known: SLINK for single-linkage and CLINK for complete-linkage clustering.Cluster dissimilarity
In order to decide which clusters should be combined (for agglomerative), or where a cluster should be split (for divisive), a measure of dissimilarity between sets of observations is required. In most methods of hierarchical clustering, this is achieved by use of an appropriate metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
(a measure of distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets.
Metric
The choice of an appropriate metric will influence the shape of the clusters, as some elements may be close to one another according to one distance and farther away according to another. For example, in a 2-dimensional space, the distance between the point (1,0) and the origin (0,0) is always 1 according to the usual norms, but the distance between the point (1,1) and the origin (0,0) can be 2,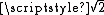 or 1 under Manhattan distance, Euclidean distance or maximum distance respectively.
or 1 under Manhattan distance, Euclidean distance or maximum distance respectively.Some commonly used metrics for hierarchical clustering are:
| Names | Formula |
|---|---|
| Euclidean distance Euclidean distance In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space... |
|
| squared Euclidean distance | |
| Manhattan distance | |
| maximum distance | |
| Mahalanobis distance Mahalanobis distance In statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936. It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown sample set to a known one. It differs from Euclidean... |
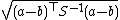 where S is the covariance matrix where S is the covariance matrixCovariance matrix In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector... |
| cosine similarity Cosine similarity Cosine similarity is a measure of similarity between two vectors by measuring the cosine of the angle between them. The cosine of 0 is 1, and less than 1 for any other angle. The cosine of the angle between two vectors thus determines whether two vectors are pointing in roughly the same... |
|-
|}
For text or other non-numeric data, metrics such as the Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
or Levenshtein distance
Levenshtein distance
In information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences...
are often used.
A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance.
Linkage criteria
The linkage criteria determines the distance between sets of observations as a function of the pairwise distances between observations.Some commonly used linkage criteria between two sets of observations A and B are:
| Names | Formula |
|---|---|
| Maximum or complete linkage clustering | 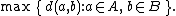 |
| Minimum or single-linkage clustering | 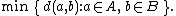 |
| Mean or average linkage clustering, or UPGMA UPGMA UPGMA is a simple agglomerative or hierarchical clustering method used in bioinformatics for the creation of phenetic trees... |
|
| Minimum energy clustering Energy distance Energy distance is a statistical distance between probability distributions. If X and Y are independent random vectors in Rd, with cumulative distribution functions F and G respectively, then the energy distance between the distributions F and G is definedwhere X, X' are independent and identically... |
where d is the chosen metric. Other linkage criteria include:
- The sum of all intra-cluster variance.
- The increase in variance for the cluster being merged ( Ward's criterion).
- The probability that candidate clusters spawn from the same distribution function (V-linkage).
Discussion
Hierarchical clustering has the distinct advantage that any valid measure of distance can be used. In fact, the observations themselves are not required: all that is used is a matrix of distances.
Example for Agglomerative Clustering
For example, suppose this data is to be clustered, and the Euclidean distanceEuclidean distanceIn mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
is the distance metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
.
Cutting the tree at a given height will give a partitioning clustering at a selected precision. In this example, cutting after the second row will yield clusters {a} {b c} {d e} {f}. Cutting after the third row will yield clusters {a} {b c} {d e f}, which is a coarser clustering, with a smaller number of larger clusters.
The hierarchical clustering dendrogramDendrogramA dendrogram is a tree diagram frequently used to illustrate the arrangement of the clusters produced by hierarchical clustering...
would be as such:
This method builds the hierarchy from the individual elements by progressively merging clusters. In our example, we have six elements {a} {b} {c} {d} {e} and {f}. The first step is to determine which elements to merge in a cluster. Usually, we want to take the two closest elements, according to the chosen distance.
Optionally, one can also construct a distance matrixDistance matrixIn mathematics, computer science and graph theory, a distance matrix is a matrix containing the distances, taken pairwise, of a set of points...
at this stage, where the number in the i-th row j-th column is the distance between the i-th and j-th elements. Then, as clustering progresses, rows and columns are merged as the clusters are merged and the distances updated. This is a common way to implement this type of clustering, and has the benefit of caching distances between clusters. A simple agglomerative clustering algorithm is described in the single-linkage clustering page; it can easily be adapted to different types of linkage (see below).
Suppose we have merged the two closest elements b and c, we now have the following clusters {a}, {b, c}, {d}, {e} and {f}, and want to merge them further. To do that, we need to take the distance between {a} and {b c}, and therefore define the distance between two clusters.
Usually the distance between two clusters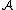 and
and 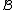 is one of the following:
is one of the following:
- The maximum distance between elements of each cluster (also called complete-linkage clusteringComplete-linkage clusteringIn cluster analysis, complete linkage or farthest neighbour is a method of calculating distances between clusters in agglomerative hierarchical clustering...
):
-
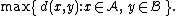
- The minimum distance between elements of each cluster (also called single-linkage clustering):
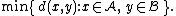
- The mean distance between elements of each cluster (also called average linkage clustering, used e.g. in UPGMAUPGMAUPGMA is a simple agglomerative or hierarchical clustering method used in bioinformatics for the creation of phenetic trees...
):
- The mean distance between elements of each cluster (also called average linkage clustering, used e.g. in UPGMA
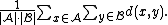
- The sum of all intra-cluster variance.
- The increase in variance for the cluster being merged ( Ward's method
In statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchyHierarchyA hierarchy is an arrangement of items in which the items are represented as being "above," "below," or "at the same level as" one another...
of clusters. Strategies for hierarchical clustering generally fall into two types:- Agglomerative: This is a "bottom up" approach: each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy.
- Divisive: This is a "top down" approach: all observations start in one cluster, and splits are performed recursively as one moves down the hierarchy.
In general, the merges and splits are determined in a greedyGreedy algorithmA greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
manner. The results of hierarchical clustering are usually presented in a dendrogramDendrogramA dendrogram is a tree diagram frequently used to illustrate the arrangement of the clusters produced by hierarchical clustering...
.
In the general case, the complexity of agglomerative clustering is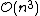 , which makes them too slow for large data sets. Divisive clustering with an exhaustive search is
, which makes them too slow for large data sets. Divisive clustering with an exhaustive search is 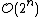 , which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity
, which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity 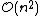 are known: SLINK for single-linkage and CLINK for complete-linkage clustering.
are known: SLINK for single-linkage and CLINK for complete-linkage clustering.
Cluster dissimilarity
In order to decide which clusters should be combined (for agglomerative), or where a cluster should be split (for divisive), a measure of dissimilarity between sets of observations is required. In most methods of hierarchical clustering, this is achieved by use of an appropriate metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
(a measure of distanceDistanceDistance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets.
Metric
The choice of an appropriate metric will influence the shape of the clusters, as some elements may be close to one another according to one distance and farther away according to another. For example, in a 2-dimensional space, the distance between the point (1,0) and the origin (0,0) is always 1 according to the usual norms, but the distance between the point (1,1) and the origin (0,0) can be 2,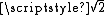 or 1 under Manhattan distance, Euclidean distance or maximum distance respectively.
or 1 under Manhattan distance, Euclidean distance or maximum distance respectively.
Some commonly used metrics for hierarchical clustering are:Names Formula Euclidean distance Euclidean distanceIn mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...squared Euclidean distance Manhattan distance maximum distance Mahalanobis distance Mahalanobis distanceIn statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936. It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown sample set to a known one. It differs from Euclidean...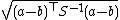 where S is the covariance matrixCovariance matrixIn probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
where S is the covariance matrixCovariance matrixIn probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...cosine similarity Cosine similarityCosine similarity is a measure of similarity between two vectors by measuring the cosine of the angle between them. The cosine of 0 is 1, and less than 1 for any other angle. The cosine of the angle between two vectors thus determines whether two vectors are pointing in roughly the same...
|-
|}
For text or other non-numeric data, metrics such as the Hamming distanceHamming distanceIn information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
or Levenshtein distanceLevenshtein distanceIn information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences...
are often used.
A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance.
Linkage criteria
The linkage criteria determines the distance between sets of observations as a function of the pairwise distances between observations.
Some commonly used linkage criteria between two sets of observations A and B are:Names Formula Maximum or complete linkage clustering 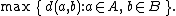
Minimum or single-linkage clustering 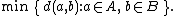
Mean or average linkage clustering, or UPGMA UPGMAUPGMA is a simple agglomerative or hierarchical clustering method used in bioinformatics for the creation of phenetic trees...Minimum energy clustering Energy distanceEnergy distance is a statistical distance between probability distributions. If X and Y are independent random vectors in Rd, with cumulative distribution functions F and G respectively, then the energy distance between the distributions F and G is definedwhere X, X' are independent and identically...
where d is the chosen metric. Other linkage criteria include:
- The sum of all intra-cluster variance.
- The increase in variance for the cluster being merged ( Ward's criterion).
- The probability that candidate clusters spawn from the same distribution function (V-linkage).
Discussion
Hierarchical clustering has the distinct advantage that any valid measure of distance can be used. In fact, the observations themselves are not required: all that is used is a matrix of distances.
Example for Agglomerative Clustering
For example, suppose this data is to be clustered, and the Euclidean distanceEuclidean distanceIn mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
is the distance metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
.
Cutting the tree at a given height will give a partitioning clustering at a selected precision. In this example, cutting after the second row will yield clusters {a} {b c} {d e} {f}. Cutting after the third row will yield clusters {a} {b c} {d e f}, which is a coarser clustering, with a smaller number of larger clusters.
The hierarchical clustering dendrogramDendrogramA dendrogram is a tree diagram frequently used to illustrate the arrangement of the clusters produced by hierarchical clustering...
would be as such:
This method builds the hierarchy from the individual elements by progressively merging clusters. In our example, we have six elements {a} {b} {c} {d} {e} and {f}. The first step is to determine which elements to merge in a cluster. Usually, we want to take the two closest elements, according to the chosen distance.
Optionally, one can also construct a distance matrixDistance matrixIn mathematics, computer science and graph theory, a distance matrix is a matrix containing the distances, taken pairwise, of a set of points...
at this stage, where the number in the i-th row j-th column is the distance between the i-th and j-th elements. Then, as clustering progresses, rows and columns are merged as the clusters are merged and the distances updated. This is a common way to implement this type of clustering, and has the benefit of caching distances between clusters. A simple agglomerative clustering algorithm is described in the single-linkage clustering page; it can easily be adapted to different types of linkage (see below).
Suppose we have merged the two closest elements b and c, we now have the following clusters {a}, {b, c}, {d}, {e} and {f}, and want to merge them further. To do that, we need to take the distance between {a} and {b c}, and therefore define the distance between two clusters.
Usually the distance between two clusters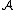 and
and 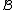 is one of the following:
is one of the following:
- The maximum distance between elements of each cluster (also called complete-linkage clusteringComplete-linkage clusteringIn cluster analysis, complete linkage or farthest neighbour is a method of calculating distances between clusters in agglomerative hierarchical clustering...
):
-
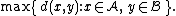
- The minimum distance between elements of each cluster (also called single-linkage clustering):
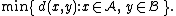
- The mean distance between elements of each cluster (also called average linkage clustering, used e.g. in UPGMAUPGMAUPGMA is a simple agglomerative or hierarchical clustering method used in bioinformatics for the creation of phenetic trees...
):
- The mean distance between elements of each cluster (also called average linkage clustering, used e.g. in UPGMA
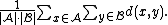
Each agglomeration occurs at a greater distance between clusters than the previous agglomeration, and one can decide to stop clustering either when the clusters are too far apart to be merged (distance criterion) or when there is a sufficiently small number of clusters (number criterion).
Free
- RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
has several functions for hierarchical clustering: see CRAN Task View: Cluster Analysis & Finite Mixture Models for more information. - OrangeOrange (software)Orange is a component-based data mining and machine learning software suite, featuring friendly yet powerful and flexible visual programming front-end for explorative data analysis and visualization, and Python bindings and libraries for scripting...
, a free data mining software suite, module orngClustering for scripting in PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
, or cluster analysis through visual programming. - hcluster is PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
software, based on NumPy, which supports hierarchical clustering and plotting. - Cluster 3.0 provides a nice Graphical User InterfaceGraphical user interfaceIn computing, a graphical user interface is a type of user interface that allows users to interact with electronic devices with images rather than text commands. GUIs can be used in computers, hand-held devices such as MP3 players, portable media players or gaming devices, household appliances and...
to access to different clustering routines and is available for Windows, Mac OS X, Linux, Unix. See: http://bonsai.hgc.jp/~mdehoon/software/cluster/ - ELKIEnvironment for DeveLoping KDD-Applications Supported by Index-StructuresELKI is a knowledge discovery in databases software framework developed for use in research and teaching by the database systems research unit of Professor Hans-Peter Kriegel at the Ludwig Maximilian University of Munich, Germany...
includes multiple hierarchical clustering algorithms. - figue A JavaScriptJavaScriptJavaScript is a prototype-based scripting language that is dynamic, weakly typed and has first-class functions. It is a multi-paradigm language, supporting object-oriented, imperative, and functional programming styles....
package that implements some agglomerative clustering functions (single-linkage, complete-linkage, average-linkage) and functions to visualize clustering output (e.g. dendograms) (Online demo). - MultiDendrograms An open sourceOpen sourceThe term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
application for variable-group agglomerative hierarchical clustering, with graphical user interfaceGraphical user interfaceIn computing, a graphical user interface is a type of user interface that allows users to interact with electronic devices with images rather than text commands. GUIs can be used in computers, hand-held devices such as MP3 players, portable media players or gaming devices, household appliances and...
. - CrimeStatCrimeStatCrimeStat is a Windows-based spatial statistic software program that conducts spatial and statistical analysis and is designed to interface with a Geographic Information System. The program is developed by Ned Levine & Associates, with funding by the National Institute of Justice...
implements two hierarchical clustering routines, a nearest neighbor (Nnh) and a risk-adjusted(Rnnh). - Complete C# DEMO implemented as visual studio project that includes real text files processing, building of document-term matrix with stop words filtering and stemming. Same site offers comparison with other algorithms.
Commercial
- Software for analyzing multivariate data with instant response using Hierarchical clustering
- SASSAS SystemSAS is an integrated system of software products provided by SAS Institute Inc. that enables programmers to perform:* retrieval, management, and mining* report writing and graphics* statistical analysis...
CLUSTER
See also
- Cluster analysis
- CURE data clustering algorithmCURE data clustering algorithmCURE is an efficient data clustering algorithm for large databases that is more robust to outliers and identifies clusters having non-spherical shapes and wide variances in size.- Drawbacks of traditional algorithms :...
- DendrogramDendrogramA dendrogram is a tree diagram frequently used to illustrate the arrangement of the clusters produced by hierarchical clustering...
- Determining the number of clusters in a data setDetermining the number of clusters in a data setDetermining the number of clusters in a data set, a quantity often labeled k as in the k-means algorithm, is a frequent problem in data clustering, and is a distinct issue from the process of actually solving the clustering problem....
- Hierarchical clustering of networks
- Nearest-neighbor chain algorithmNearest-neighbor chain algorithmIn the theory of cluster analysis, the nearest-neighbor chain algorithm is a method that can be used to perform several types of agglomerative hierarchical clustering, using an amount of memory that is linear in the number of points to be clustered and an amount of time linear in the number of...
- Numerical taxonomyNumerical taxonomyNumerical taxonomy is a classification system in biological systematics which deals with the grouping by numerical methods of taxonomic units based on their character states.. It aims to create a taxonomy using numeric algorithms like cluster analysis rather than using subjective evaluation of...
- OPTICS algorithmOPTICS algorithmOPTICS is an algorithm for finding density-based clusters in spatial data. It was presented by Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel and Jörg Sander....

