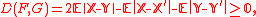Energy distance
Encyclopedia
Energy distance is a statistical distance
between probability distributions. If X and Y are independent random vectors in Rd, with cumulative distribution function
s F and G respectively, then the energy distance between the distributions F and G is defined
where X, X' are independent and identically distributed (iid), Y, Y' are iid,
is expected value, and || . || denotes the length of a vector. Energy distance characterizes the equality of distributions: D(F,G) = 0 if and only if X and Y are identically distributed.
Energy distance for statistical applications was introduced in 1985 by Gábor J. Székely
who proved that for real valued random variables this distance is exactly twice of Harald Cramér
's distance :
For a simple proof of this equivalence see Székely and Rizzo (2005). In higher dimensions, however, the two distances are different because the energy distance is rotation invariant while Cramér's distance is not. (Notice that Cramér's distance is not the same as the distribution-free Cramer-von-Mises criterion
.)
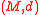be a metric space
with its Borel sigma algebra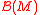
. Let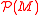 
denote the collection of all probability measure
s on the measurable space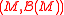
. If μ and ν are probability measures in 
then the energy distance of μ and ν can be defined as
If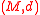
is isometric
to a subset of a Hilbert space
then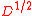
is a metric
thus the energy distance is zero if and only if X and Y are identically distributed.
in the 1980s when he was giving colloquium lectures in Budapest, Hungary and at MIT, Yale, and Columbia. This concept is based on the notion of Newton’s potential energy
. The idea is to consider statistical observations as heavenly bodies
governed by a statistical potential energy
which is zero only when an underlying statistical null hypothesis
is true. Energy statistics are functions of distances between statistical observations.
s: μ = v . For statistical samples from X and Y:
the following arithmetic averages of distances are computed between the X and the Y samples:
The E-statistic of the underlying null hypothesis is defined as follows:
One can prove that Εn,m(X,Y) ≥ 0 and that the corresponding population value, E(X,Y):= D(μ,ν), is zero if and only if X and Y have the same distribution (μ=ν). Under this null hypothesis the test statistic
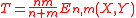
converges in distribution
to a quadratic form of independent standard normal random variables. Under the alternative hypothesis T tends to infinity. This makes it possible to construct a consistent statistical test, the energy test for equal distributions.
The E-coefficient of inhomogeneity can also be introduced. This is always between 0 and 1 and is defined as
where
denotes the expected value
. H = 0 exactly when X and Y have the same distribution.
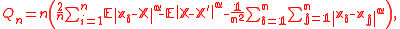
where X and X' are independent and identically distributed according to the hypothesized distribution, and
. The only required condition is that X has finite 
moment under the null hypothesis. Under the null hypothesis 
, and the asymptotic distribution of Qn is a quadratic form of centered Gaussian random variables. Under an alternative hypothesis, Qn tends to infinity stochastically, and thus determines a statistically consistent test. For most applications the exponent 1 (Euclidean distance) can be applied. The important special case of testing multivariate normality is implemented in the energy package for R. Tests are also developed for heavy tailed distributions such as Pareto (power law
), or stable distributions by application of exponents in (0,1).
Applications of energy statistics are implemented in the open source energy package for R
.
Statistical distance
In statistics, probability theory, and information theory, a statistical distance quantifies the distance between two statistical objects, which can be two samples, two random variables, or two probability distributions, for example.-Metrics:...
between probability distributions. If X and Y are independent random vectors in Rd, with cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s F and G respectively, then the energy distance between the distributions F and G is defined
where X, X' are independent and identically distributed (iid), Y, Y' are iid,
is expected value, and || . || denotes the length of a vector. Energy distance characterizes the equality of distributions: D(F,G) = 0 if and only if X and Y are identically distributed.Energy distance for statistical applications was introduced in 1985 by Gábor J. Székely
Gábor J. Székely
Gábor J. Székely is a Hungarian-American statistician/mathematician best known for introducing E-statistics or energy statistics [see E-statistics or Package energy in R ], e.g...
who proved that for real valued random variables this distance is exactly twice of Harald Cramér
Harald Cramér
Harald Cramér was a Swedish mathematician, actuary, and statistician, specializing in mathematical statistics and probabilistic number theory. He was once described by John Kingman as "one of the giants of statistical theory".-Early life:Harald Cramér was born in Stockholm, Sweden on September...
's distance :
-
.
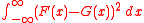For a simple proof of this equivalence see Székely and Rizzo (2005). In higher dimensions, however, the two distances are different because the energy distance is rotation invariant while Cramér's distance is not. (Notice that Cramér's distance is not the same as the distribution-free Cramer-von-Mises criterion
Cramer-von-Mises criterion
In statistics the Cramér–von Mises criterion is a criterion used for judging the goodness of fit of a cumulative distribution function F^* compared to a given empirical distribution function F_n, or for comparing two empirical distributions. It is also used as a part of other algorithms, such as...
.)
Generalization to metric spaces
Rotation invariance makes it possible to generalize the notion of energy distance to probability distributions on metric spaces. Let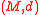 be a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
with its Borel sigma algebra
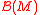. Let 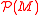denote the collection of all probability measureProbability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s on the measurable space
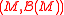. If μ and ν are probability measures in then the energy distance of μ and ν can be defined as
If
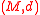is isometricIsometric
The term isometric comes from the Greek for "having equal measurement".isometric may mean:* Isometric projection , a method for the visual representation of three-dimensional objects in two dimensions; a form of orthographic projection, or more specifically, an axonometric projection.* Isometry and...
to a subset of a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
then
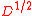is a metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
thus the energy distance is zero if and only if X and Y are identically distributed.
Energy statistics
A related statistical concept, the notion of E-statistic or energy-statistic was introduced by Gábor J. SzékelyGábor J. Székely
Gábor J. Székely is a Hungarian-American statistician/mathematician best known for introducing E-statistics or energy statistics [see E-statistics or Package energy in R ], e.g...
in the 1980s when he was giving colloquium lectures in Budapest, Hungary and at MIT, Yale, and Columbia. This concept is based on the notion of Newton’s potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
. The idea is to consider statistical observations as heavenly bodies
Heavenly Body
is a yaoi manga anthology by Takashi Kanzaki and published by Daitosha. It is licensed in English by Aurora Publishing, which released the manga in August 2008.-Reception:...
governed by a statistical potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
which is zero only when an underlying statistical null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
is true. Energy statistics are functions of distances between statistical observations.
Testing for equal distributions
Consider the null hypothesis that two random variables, X and Y, have the same probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s: μ = v . For statistical samples from X and Y:
- x1,…,xn and y1,…,ym,
the following arithmetic averages of distances are computed between the X and the Y samples:
- A:= (1/nm)∑|xi – yj|, B:= (1/n2)∑|xi – xj|, C:= (1/m2)∑|yi – yj|.
The E-statistic of the underlying null hypothesis is defined as follows:
- Εn,m(X,Y):= 2A – B – C.
One can prove that Εn,m(X,Y) ≥ 0 and that the corresponding population value, E(X,Y):= D(μ,ν), is zero if and only if X and Y have the same distribution (μ=ν). Under this null hypothesis the test statistic
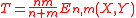
converges in distribution
Convergence of random variables
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...
to a quadratic form of independent standard normal random variables. Under the alternative hypothesis T tends to infinity. This makes it possible to construct a consistent statistical test, the energy test for equal distributions.
The E-coefficient of inhomogeneity can also be introduced. This is always between 0 and 1 and is defined as
where
denotes the expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
. H = 0 exactly when X and Y have the same distribution.
Goodness-of-fit
A multivariate goodness-of-fit measure is defined for distributions in arbitrary dimension (not restricted by sample size). The energy goodness-of-fit statistic is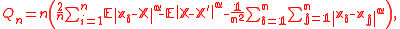where X and X' are independent and identically distributed according to the hypothesized distribution, and
. The only required condition is that X has finite moment under the null hypothesis. Under the null hypothesis , and the asymptotic distribution of Qn is a quadratic form of centered Gaussian random variables. Under an alternative hypothesis, Qn tends to infinity stochastically, and thus determines a statistically consistent test. For most applications the exponent 1 (Euclidean distance) can be applied. The important special case of testing multivariate normality is implemented in the energy package for R. Tests are also developed for heavy tailed distributions such as Pareto (power lawPower law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
), or stable distributions by application of exponents in (0,1).
Applications
Applications include- Hierarchical clusteringHierarchical clusteringIn statistics, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:...
(a generalization of Ward's method) - Testing multivariate normality
- Testing the multi-sample hypothesis of equal distributions,
- Change point detectionChange detectionIn statistical analysis, change detection tries to identify changes in the probability distribution of a stochastic process or time series. In general the problem concerns both detecting whether or not a change has occurred, or whether several changes might have occurred, and identifying the times...
- Multivariate independence:
- distance correlationDistance correlationIn statistics and in probability theory, distance correlation is a measure of statistical dependence between two random variables or two random vectors of arbitrary, not necessarily equal dimension. Its important property is that this measure of dependence is zero if and only if the random...
, - Brownian covariance.
- Scoring rules:
- Gneiting and Raftery apply energy distance to develop a new and very general type of proper scoring rule for probabilistic predictions, the energy score.
Applications of energy statistics are implemented in the open source energy package for R
R (programming language)
R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
.