
Completely Hausdorff space
Encyclopedia
In topology
, an Urysohn space, or T2½ space, is a topological space
in which any two distinct points can be separated by closed neighborhoods. A completely Hausdorff space, or functionally Hausdorff space, is a topological space in which any two distinct points can be separated by a continuous function
. These conditions are separation axiom
s that are somewhat stronger than the more familiar Hausdorff axiom
T2.
. Let x and y be points in X.
A Urysohn space, or T2½ space, is a space in which any two distinct points can be separated by closed neighborhoods.
A completely Hausdorff space, or functionally Hausdorff space, is a space in which any two distinct points can be separated by a function.
for more on this issue.
.
One can also show that every regular Hausdorff space is Urysohn and every Tychonoff space
(=completely regular Hausdorff space) is completely Hausdorff. In summary we have the following implications:
One can find counterexamples showing that none of these implications reverse.
generated by the union
of the usual Euclidean topology
and the cocountable topology
. Sets are open
in this topology if and only if they are of the form U \ A where U is open in the Euclidean topology and A is countable. This space is completely Hausdorff and Urysohn, but not regular (and thus not Tychonoff).
There are obscure examples of spaces which are Hausdorff but not Urysohn, and spaces which are Urysohn but not completely Hausdorff or regular Hausdorff. For details see Steen and Seebach.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, an Urysohn space, or T2½ space, is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
in which any two distinct points can be separated by closed neighborhoods. A completely Hausdorff space, or functionally Hausdorff space, is a topological space in which any two distinct points can be separated by a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. These conditions are separation axiom
Separation axiom
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
s that are somewhat stronger than the more familiar Hausdorff axiom
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
T2.
Definitions
Suppose that X is a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. Let x and y be points in X.
- We say that x and y can be separated by closed neighborhoods if there exists a closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
neighborhood U of x and a closed neighborhood V of y such that U and V are disjoint (U ∩ V = ∅). (Note that a "closed neighborhood of x" is a closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
that contains an open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
containing x.) - We say that x and y can be separated by a function if there exists a continuous function f : X → [0,1] (the unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
) with f(x) = 0 and f(y) = 1.
A Urysohn space, or T2½ space, is a space in which any two distinct points can be separated by closed neighborhoods.
A completely Hausdorff space, or functionally Hausdorff space, is a space in which any two distinct points can be separated by a function.
Naming conventions
The study of separation axioms is notorious for conflicts with naming conventions used. The definitions used in this article are those given by Willard (1970) and are the more modern definitions. Steen and Seebach (1970) and various other authors reverse the definition of completely Hausdorff spaces and Urysohn spaces. Readers of textbooks in topology must be sure to check the definitions used by the author. See History of the separation axiomsHistory of the separation axioms
In general topology, the separation axioms have had a convoluted history, with many competing meanings for the same term, and many competing terms for the same concept.- Origins :...
for more on this issue.
Relation to other separation axioms
It is an easy exercise to show that any two points which can be separated by a function can be separated by closed neighborhoods. If they can be separated by closed neighborhoods then clearly they can be separated by neighborhoods. It follows that every completely Hausdorff space is Urysohn and every Urysohn space is HausdorffHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
.
One can also show that every regular Hausdorff space is Urysohn and every Tychonoff space
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
(=completely regular Hausdorff space) is completely Hausdorff. In summary we have the following implications:
| Tychonoff Tychonoff space In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms.... (T3½) |
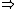 |
regular Hausdorff Regular space In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C... (T3) |
||||
 |
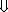 |
|||||
| completely Hausdorff | 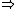 |
Urysohn (T2½) | 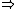 |
Hausdorff Hausdorff space In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently... (T2) |
 |
T1 T1 space In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points... |
One can find counterexamples showing that none of these implications reverse.
Examples
The cocountable extension topology is the topology on the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
generated by the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of the usual Euclidean topology
Euclidean topology
In mathematics, and especially general topology, the Euclidean topology is an example of a topology given to the set of real numbers, denoted by R...
and the cocountable topology
Cocountable topology
The cocountable topology or countable complement topology on any set X consists of the empty set and all cocountable subsets of X, that is all sets whose complement in X is countable...
. Sets are open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in this topology if and only if they are of the form U \ A where U is open in the Euclidean topology and A is countable. This space is completely Hausdorff and Urysohn, but not regular (and thus not Tychonoff).
There are obscure examples of spaces which are Hausdorff but not Urysohn, and spaces which are Urysohn but not completely Hausdorff or regular Hausdorff. For details see Steen and Seebach.

