
Completely metrizable space
Encyclopedia
In mathematics
, a completely metrizable space (complete topological space or topologically complete space) is a topological space
(X, T) for which there exists at least one metric
d on X such that (X, d) is a complete metric space
and d induces the topology T. This is equivalent to the condition that X is a Gδ
in its Stone–Čech compactification
βX.
The set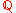 of rational numbers is an example of a topological space that is metrizable but not completely metrizable.
of rational numbers is an example of a topological space that is metrizable but not completely metrizable.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a completely metrizable space (complete topological space or topologically complete space) is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
(X, T) for which there exists at least one metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
d on X such that (X, d) is a complete metric space
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
and d induces the topology T. This is equivalent to the condition that X is a Gδ
G-delta set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
in its Stone–Čech compactification
Stone–Cech compactification
In the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
βX.
The set
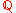 of rational numbers is an example of a topological space that is metrizable but not completely metrizable.
of rational numbers is an example of a topological space that is metrizable but not completely metrizable.

