
Complex conjugate vector space
Encyclopedia
In mathematics
, the (formal) complex conjugate of a complex vector space
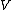 is the complex vector space
is the complex vector space  consisting of all formal complex conjugate
consisting of all formal complex conjugate
s of elements of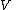 . That is,
. That is, 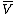 is a vector space whose elements are in one-to-one correspondence
is a vector space whose elements are in one-to-one correspondence
with the elements of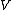 :
: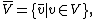
with the following rules for addition
and scalar multiplication
: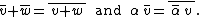
Here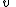 and
and 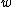 are vectors in
are vectors in 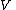 ,
, 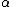 is a complex number, and
is a complex number, and 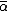 denotes the complex conjugate of
denotes the complex conjugate of  .
.
More concretely, the complex conjugate is the same underlying real vector space (same set of points, same vector addition and real scalar multiplication) with the conjugate linear complex structure
J (different multiplication by i).
In the case where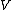 is a linear subspace
is a linear subspace
of , the formal complex conjugate
, the formal complex conjugate 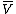 is naturally isomorphic to the actual complex conjugate subspace of
is naturally isomorphic to the actual complex conjugate subspace of 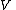 in
in 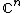 .
.
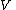 and
and 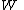 are complex vector spaces, a function
are complex vector spaces, a function 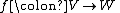 is antilinear if
is antilinear if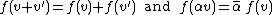
for all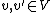 and
and 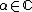 .
.
One reason to consider the vector space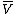 is that it makes antilinear maps into linear maps. Specifically, if
is that it makes antilinear maps into linear maps. Specifically, if 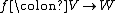 is an antilinear map, then the corresponding map
is an antilinear map, then the corresponding map 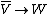 defined by
defined by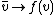
is linear. Conversely, any linear map defined on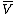 gives rise to an antilinear map on
gives rise to an antilinear map on 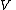 .
.
One way of thinking about this correspondence is that the map defined by
defined by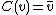
is an antilinear bijection. Thus if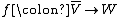 if linear, then composition
if linear, then composition
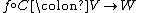 is antilinear, and vice versa.
is antilinear, and vice versa.
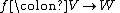 induces a conjugate linear map
induces a conjugate linear map 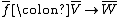 , defined by the formula
, defined by the formula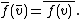
The conjugate linear map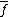 is linear. Moreover, the identity map
is linear. Moreover, the identity map
on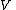 induces the identity map
induces the identity map 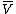 , and
, and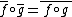
for any two linear maps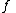 and
and 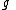 . Therefore, the rules
. Therefore, the rules 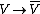 and
and 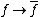 define a functor
define a functor
from the category
of complex vector spaces to itself.
If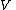 and
and 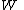 are finite-dimensional and the map
are finite-dimensional and the map 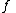 is described by the complex matrix
is described by the complex matrix
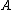 with respect to the bases
with respect to the bases 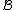 of
of 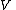 and
and 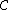 of
of  , then the map
, then the map  is described by the complex conjugate of
is described by the complex conjugate of  with respect to the bases
with respect to the bases  of
of 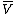 and
and 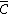 of
of 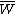 .
.
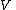 and
and 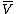 have the same dimension over the complex numbers and are therefore isomorphic
have the same dimension over the complex numbers and are therefore isomorphic
as complex vector spaces. However, there is no natural isomorphism from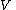 to
to 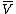 . (The map
. (The map 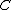 is not an isomorphism, since it is antilinear.)
is not an isomorphism, since it is antilinear.)
The double conjugate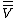 is naturally isomorphic to
is naturally isomorphic to 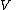 , with the isomorphism
, with the isomorphism 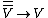 defined by
defined by
Usually the double conjugate of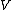 is simply identified with
is simply identified with  .
.
 (either finite or infinite dimensional), its complex conjugate
(either finite or infinite dimensional), its complex conjugate 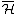 is the same vector space as its continuous dual space
is the same vector space as its continuous dual space 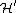 .
.
There is one-to-one antilinear correspondence between continuous linear functionals and vectors.
In other words, any continuous linear functional
on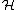 is an inner multiplication to some fixed vector, and vice versa.
is an inner multiplication to some fixed vector, and vice versa.
Thus, the complex conjugate to a vector , particularly in finite dimension case, may be denoted as
, particularly in finite dimension case, may be denoted as  (v-star, a row vector which is the conjugate transpose
(v-star, a row vector which is the conjugate transpose
to a column vector ).
).
In quantum mechanics, the conjugate to a ket vector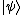 is denoted as
is denoted as 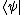 – a bra vector (see bra-ket notation
– a bra vector (see bra-ket notation
).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the (formal) complex conjugate of a complex vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
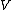 is the complex vector space
is the complex vector space  consisting of all formal complex conjugate
consisting of all formal complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
s of elements of
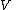 . That is,
. That is, 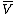 is a vector space whose elements are in one-to-one correspondence
is a vector space whose elements are in one-to-one correspondenceBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
with the elements of
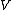 :
: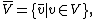
with the following rules for addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
:
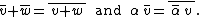
Here
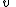 and
and 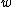 are vectors in
are vectors in 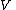 ,
, 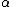 is a complex number, and
is a complex number, and 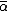 denotes the complex conjugate of
denotes the complex conjugate of  .
.More concretely, the complex conjugate is the same underlying real vector space (same set of points, same vector addition and real scalar multiplication) with the conjugate linear complex structure
Linear complex structure
In mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.Complex structures have...
J (different multiplication by i).
In the case where
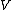 is a linear subspace
is a linear subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of
 , the formal complex conjugate
, the formal complex conjugate 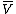 is naturally isomorphic to the actual complex conjugate subspace of
is naturally isomorphic to the actual complex conjugate subspace of 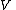 in
in 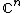 .
.Antilinear maps
If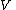 and
and 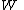 are complex vector spaces, a function
are complex vector spaces, a function 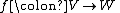 is antilinear if
is antilinear if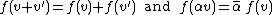
for all
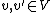 and
and 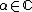 .
.One reason to consider the vector space
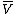 is that it makes antilinear maps into linear maps. Specifically, if
is that it makes antilinear maps into linear maps. Specifically, if 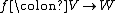 is an antilinear map, then the corresponding map
is an antilinear map, then the corresponding map 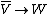 defined by
defined by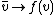
is linear. Conversely, any linear map defined on
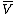 gives rise to an antilinear map on
gives rise to an antilinear map on 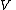 .
.One way of thinking about this correspondence is that the map
 defined by
defined by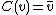
is an antilinear bijection. Thus if
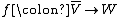 if linear, then composition
if linear, then compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
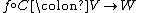 is antilinear, and vice versa.
is antilinear, and vice versa.Conjugate linear maps
Any linear map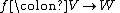 induces a conjugate linear map
induces a conjugate linear map 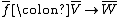 , defined by the formula
, defined by the formula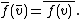
The conjugate linear map
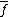 is linear. Moreover, the identity map
is linear. Moreover, the identity mapIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on
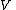 induces the identity map
induces the identity map 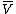 , and
, and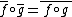
for any two linear maps
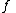 and
and 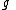 . Therefore, the rules
. Therefore, the rules 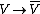 and
and 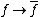 define a functor
define a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of complex vector spaces to itself.
If
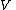 and
and 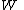 are finite-dimensional and the map
are finite-dimensional and the map 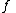 is described by the complex matrix
is described by the complex matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
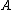 with respect to the bases
with respect to the bases 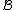 of
of 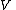 and
and 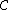 of
of  , then the map
, then the map  is described by the complex conjugate of
is described by the complex conjugate of  with respect to the bases
with respect to the bases  of
of 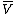 and
and 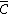 of
of 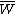 .
.Structure of the conjugate
The vector spaces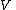 and
and 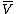 have the same dimension over the complex numbers and are therefore isomorphic
have the same dimension over the complex numbers and are therefore isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
as complex vector spaces. However, there is no natural isomorphism from
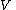 to
to 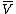 . (The map
. (The map 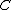 is not an isomorphism, since it is antilinear.)
is not an isomorphism, since it is antilinear.)The double conjugate
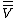 is naturally isomorphic to
is naturally isomorphic to 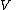 , with the isomorphism
, with the isomorphism 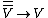 defined by
defined by
Usually the double conjugate of
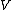 is simply identified with
is simply identified with  .
.Complex conjugate of a Hilbert space
Given a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
 (either finite or infinite dimensional), its complex conjugate
(either finite or infinite dimensional), its complex conjugate 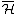 is the same vector space as its continuous dual space
is the same vector space as its continuous dual space 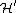 .
.There is one-to-one antilinear correspondence between continuous linear functionals and vectors.
In other words, any continuous linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on
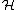 is an inner multiplication to some fixed vector, and vice versa.
is an inner multiplication to some fixed vector, and vice versa.Thus, the complex conjugate to a vector
 , particularly in finite dimension case, may be denoted as
, particularly in finite dimension case, may be denoted as  (v-star, a row vector which is the conjugate transpose
(v-star, a row vector which is the conjugate transposeConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
to a column vector
 ).
).In quantum mechanics, the conjugate to a ket vector
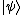 is denoted as
is denoted as 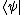 – a bra vector (see bra-ket notation
– a bra vector (see bra-ket notationBra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
).

