Complex squaring map
Encyclopedia
In mathematics, the complex squaring map, a polynomial
mapping of degree two
, is a simple and accessible demonstration of chaos
in dynamical systems. It can be constructed by performing the following steps:
This repetition (iteration) produces a sequence of complex numbers that can be described by their complex angle alone. Any choice of starting angle that satisfies (1) above will produce an extremely complicated sequence of angles, that belies the simplicity of the steps. In fact, it can be shown that the sequence will be chaotic
, i.e. it is sensitive to the detailed choice of starting angle.
(also known as the 2x mod 1 map). As the initial value z0 has been chosen so that its argument is not a rational multiple of π, the forward orbit
of zn cannot repeat itself and become periodic.
More formally, the iteration can be written as: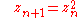
where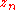
is the resulting sequence of complex numbers obtained by iterating the steps above, and 
represents the initial starting number. We can solve this iteration exactly:
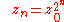
Starting with angle θ, we can write the initial term as
so that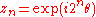 
. This makes the successive doubling of the angle clear. (This is equivalent to the relation 
.)
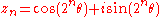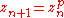is also exactly solvable as 
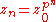. In the case p = 2, the dynamics can be mapped to the dyadic transformation, as described above, but for p > 2, we obtain a shift map in the number base p. For example, p = 10 is a decimal shift map.
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
mapping of degree two
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
, is a simple and accessible demonstration of chaos
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
in dynamical systems. It can be constructed by performing the following steps:
- Choose any complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
on the unit circleUnit circleIn mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
whose argumentArg (mathematics)In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
(complex angle) is not a rational fraction of π, - Repeatedly square that number.
This repetition (iteration) produces a sequence of complex numbers that can be described by their complex angle alone. Any choice of starting angle that satisfies (1) above will produce an extremely complicated sequence of angles, that belies the simplicity of the steps. In fact, it can be shown that the sequence will be chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
, i.e. it is sensitive to the detailed choice of starting angle.
Chaos and the complex squaring map
The informal reason why the iteration is chaotic is that the angle doubles on every iteration and doubling grows very quickly as the angle becomes ever larger, but angles which differ by multiples of 2π (radians) are identical. Thus, when the angle exceeds 2π, it must wrap to the remainder on division by 2π. Therefore the angle is transformed according to the dyadic transformationDyadic transformation
The dyadic transformation is the mapping produced by the rule...
(also known as the 2x mod 1 map). As the initial value z0 has been chosen so that its argument is not a rational multiple of π, the forward orbit
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
of zn cannot repeat itself and become periodic.
More formally, the iteration can be written as:
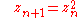
where
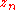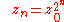
is the resulting sequence of complex numbers obtained by iterating the steps above, and represents the initial starting number. We can solve this iteration exactly:Starting with angle θ, we can write the initial term as
so that 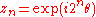. This makes the successive doubling of the angle clear. (This is equivalent to the relation 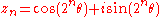.)Generalisations
This map is a special case of the complex quadratic map, which has exact solutions for many special cases. The complex map obtained by raising the previous number to any natural number power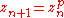 is also exactly solvable as 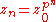. In the case p = 2, the dynamics can be mapped to the dyadic transformation, as described above, but for p > 2, we obtain a shift map in the number base p. For example, p = 10 is a decimal shift map.See also
- Chaos theoryChaos theoryChaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
- Logistic functionLogistic functionA logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
- List of chaotic maps
- Complex quadratic map