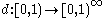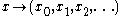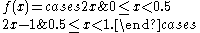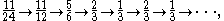The dyadic transformation (also known as the dyadic map, bit shift map, 2x mod 1 map, Bernoulli map, doubling map or sawtooth map) is the mapping

Map (mathematics)

In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...

 (i.e., recurrence relation

Recurrence relation

In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....

)

produced by the rule

.

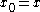
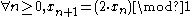Equivalently, the dyadic transformation can also be defined as the iterated function

Iterated function

In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...

 map of the piecewise linear function

The name bit shift map arises because, if the value of an iterate is written in binary notation, the next iterate is obtained by shifting the binary point one bit to the right, and if the bit to the left of the new binary point is a "one", replacing it with a zero.

The dyadic transformation provides an example of how a simple 1-dimensional map can give rise to chaos

Chaos theory

Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...

.

Relation to tent map and logistic map

The dyadic transformation is topologically conjugate to :

• the unit-height tent map
• the chaotic r=4 case of the logistic map
  Logistic map
  The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
  
  .

The r=4 case of the logistic map is 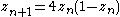; this is related to the bit shift map in variable x by

.

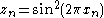There is semi-conjugacy between the dyadic transformation ( here named doubling map) and the quadratic polynomial

Complex quadratic polynomial

A complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...

.

Periodicity and non-periodicity

Because of the simple nature of the dynamics when the iterates are viewed in binary notation, it is easy to categorize the dynamics based on the initial condition:

If the initial condition is irrational (as almost all points in the unit interval are), then the dynamics are non-periodic—this follows directly from the definition of an irrational number as one with a non-repeating binary expansion. This is the chaotic case.

If x₀ is rational

Rational number

In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

 the image of x₀ contains a finite number of distinct values within [0, 1) and the forward orbit

Orbit (dynamics)

In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...

 of x₀ is eventually periodic, with period equal to the period of the binary

Binary numeral system

The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...

 expansion of x₀. Specifically, if the initial condition is a rational number with a finite binary expansion of k bits, then after k iterations the iterates reach the fixed point 0;
if the initial condition is a rational number with a k-bit transient (k≥0) followed by a q-bit sequence (q>1) that repeats itself infinitely, then after k iterations the iterates reach a cycle of length q. Thus cycles of all lengths are possible.

For example, the forward orbit of 11/24 is:

which has reached a cycle of period 2. Within any sub-interval of [0,1), no matter how small, there are therefore an infinite number of points whose orbits are eventually periodic, and an infinite number of points whose orbits are never periodic. This sensitive dependence on initial conditions is a characteristic of chaotic maps.

Solvability

The dyadic transformation is an exactly solvable model in the theory of deterministic chaos. The square-integrable eigenfunction

Eigenfunction

In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...

s of the associated transfer operator

Transfer operator

In mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...

 of the Bernoulli map are the Bernoulli polynomials. These eigenfunctions form a discrete spectrum

Discrete spectrum

In physics, an elementary explanation of a discrete spectrum is that it is an emission spectrum or absorption spectrum for which there is only an integer number of intensities. Atomic electronic absorption and emission spectrum are discrete, as contrasted with, for example, the emission spectrum...

 with eigenvalues 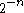for non-negative integers n. There are more general eigenvectors, which are not square-integrable, associated with a continuous spectrum

Continuous spectrum

The spectrum of a linear operator is commonly divided into three parts: point spectrum, continuous spectrum, and residual spectrum.If H is a topological vector space and A:H \to H is a linear map, the spectrum of A is the set of complex numbers \lambda such that A - \lambda I : H \to H is not...

. These are given by the Hurwitz zeta function; equivalently, linear combinations of the Hurwitz zeta give fractal, differentiable-nowhere eigenfunctions, including the Takagi function. The fractal eigenfunctions show a symmetry under the fractal groupoid

Groupoid

In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...

 of the modular group

Modular group

In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...

.

Rate of information loss and sensitive dependence on initial conditions

One hallmark of chaotic dynamics is the loss of information as simulation occurs. If we start with information on the first s bits of the initial iterate, then after m simulated iterations (m<s) we only have (s-m) bits of information remaining. Thus we lose information at the exponential rate of one bit per iteration. After s iterations, our simulation has reached the fixed point zero, regardless of the true iterate values; thus we have suffered a complete loss of information. This illustrates sensitive dependence on initial conditions—the mapping from the truncated initial condition has deviated exponentially from the mapping from the true initial condition. And since our simulation has reached a fixed point, for almost all initial conditions it will not describe the dynamics in the qualitatively correct way as chaotic.

Equivalent to the concept of information loss is the concept of information gain. In practice some real-world process may generate a sequence of values {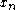} over time, but we may only be able to observe these values in truncated form. Suppose for example that = .1001101, but we only observe the truncated value .1001 . Our prediction for 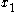is .001 . If we wait until the real-world process has generated the true 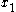value .001101, we will be able to observe the truncated value .0011, which is more accurate than our predicted value .001 . So we have received an information gain of one bit.