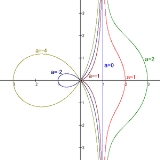
Conchoid of de Sluze
Encyclopedia
The conchoid of de Sluze is a family of plane curve
s studied in 1662 by René François Walter, baron de Sluze.
The curves are defined by the polar equation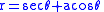
.
In cartesian coordinates
, the curves satisfy the implicit equation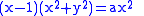
except that for a=0 the implicit form has an acnode
(0,0) not present in polar form.
They are rational, circular
, cubic plane curve
s.
These expressions have an asymptote
x=1 (for a≠0). The point most distant from the asymptote is (1+a,0). (0,0) is a crunode
for a<−1.
The area between the curve and the asymptote is, for
,
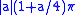
while for
, the area is
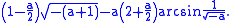
If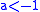
, the curve will have a loop. The area of the loop is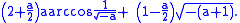
Four of the family have names of their own:
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s studied in 1662 by René François Walter, baron de Sluze.
The curves are defined by the polar equation
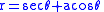.In cartesian coordinates
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, the curves satisfy the implicit equation
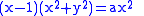
except that for a=0 the implicit form has an acnode
Acnode
An acnode is an isolated point not on a curve, but whose coordinates satisfy the equation of the curve. The term "isolated point" or "hermit point" is an equivalent term....
(0,0) not present in polar form.
They are rational, circular
Circular algebraic curve
In geometry, a circular algebraic curve is a type of plane algebraic curve determined by an equation F = 0, where F is a polynomial with real coefficients and the highest-order terms of F form a polynomial divisible by x2 + y2...
, cubic plane curve
Cubic plane curve
In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equationapplied to homogeneous coordinates x:y:z for the projective plane; or the inhomogeneous version for the affine space determined by setting z = 1 in such an equation...
s.
These expressions have an asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
x=1 (for a≠0). The point most distant from the asymptote is (1+a,0). (0,0) is a crunode
Crunode
A crunode is a point where a curve intersects itself so that both branches of the curve have distinct tangent lines.For a plane curve, defined as the locus of points f = 0, where f is a smooth function of variables x and y ranging over the real numbers, a crunode of the curve is a singularity of...
for a<−1.
The area between the curve and the asymptote is, for
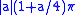
,while for
, the area is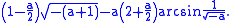If
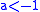, the curve will have a loop. The area of the loop is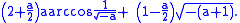Four of the family have names of their own:
- a=0, lineLine (mathematics)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
(asymptote to the rest of the family) - a=−1, cissoid of DioclesCissoid of DioclesIn geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the...
- a=−2, right strophoidStrophoidIn geometry, a strophoid is a curve generated from a given curve C and points A and O as follows: Let L be a variable line passing through O and intersecting C at K. Now let P1 and P2 be the two points on L whose distance from K is the same as the distance from A to K...
- a=−4, trisectrix of MaclaurinTrisectrix of MaclaurinIn geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the points of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the...