In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the trisectrix of Maclaurin is a cubic plane curve

Cubic plane curve

In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equationapplied to homogeneous coordinates x:y:z for the projective plane; or the inhomogeneous version for the affine space determined by setting z = 1 in such an equation...

 notable for its trisectrix

Trisectrix

In geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of...

 property, meaning it can be used to trisect an angle. It can be defined as locus of the points of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the rates of rotation is 1:3 and the lines initially coincide with the line between the two points. A generalization of this construction is called a sectrix of Maclaurin

Sectrix of Maclaurin

In geometry, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is...

. The curve is named after Colin Maclaurin

Colin Maclaurin

Colin Maclaurin was a Scottish mathematician who made important contributions to geometry and algebra. The Maclaurin series, a special case of the Taylor series, are named after him....

 who investigated the curve in 1742.

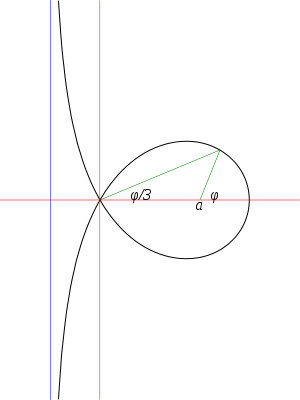
Equations

Let two lines rotate about the points and 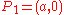so that when the line rotating about has angle 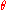with the x axis, the rotating about 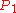has angle . Let be the point of intersection, then the angle formed by the lines at is . By the law of sines

Law of sines

In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...

,
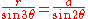
so the equation in polar coordinates is (up to translation and rotation).
The curve is therefore a member of the Conchoid of de Sluze

Conchoid of de Sluze

The conchoid of de Sluze is a family of plane curves studied in 1662 by René François Walter, baron de Sluze.The curves are defined by the polar equationr=\sec\theta+a\cos\theta \,....

 family.

In Cartesian coordinates the equation this is.

If the origin is moved to (a, 0) then a derivation similar to that given above shows that the equation of the curve in polar coordinates becomes
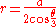
making it an example of an epispiral.

The trisection property

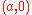Given an angle , draw a ray from whose angle with the -axis is . Draw a ray from the origin to the point where the first ray intersects the curve. Then, by the construction of the curve, the angle between the second ray and the -axis is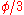

Notable points and features

The curve has an x-intercept at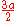 and a double point at the origin. The vertical line 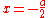is an asymptote. The curve intersects the line x = a, or the point corresponding to the trisection of a right angle, at 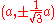. As a nodal cubic, it is of genus

Genus (mathematics)

In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...

 zero.

Relationship to other curves

The trisectrix of Maclaurin can be defined from conic sections in three ways. Specifically:

• It is the inverse
  Inverse curve
  In geometry, an inverse curve of a given curve C is the result of applying an inverse operation to C. Specifically, with respect to a fixed circle with center O and radius k the inverse of a point Q is the point P for which P lies on the ray OQ and OP·PQ = k2...
  
   with respect to the unit circle of the hyperbola
  Hyperbola
  In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
  
  

.

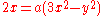• It is cissoid
  Cissoid
  In geometry, a cissoid is a curve generated from two given curves C1, C2 and a point O . Let L be a variable line passing through O and intersecting C1 at P1 and C2 at P2. Let P be the point on L so that OP = P1P2...
  
   of the circle

and the line 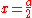relative to the origin.

• It is the pedal
  Pedal curve
  In the differential geometry of curves, a pedal curve is a curve derived by construction from a given curve ....
  
   with respect to the origin of the parabola
  Parabola
  In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
  
  

.

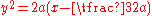In addition:

• The inverse with respect to the point 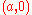is the Limaçon trisectrix
  Limaçon trisectrix
  In geometry, a limaçon trisectrix is a member of the Limaçon family of curves which has the trisectrix, or angle trisection, property...
  
  .

• The trisectrix of Maclaurin is related to the Folium of Descartes
  Folium of Descartes
  In geometry, the Folium of Descartes is an algebraic curve defined by the equationx^3 + y^3 - 3 a x y = 0 \,.It forms a loop in the first quadrant with a double point at the origin and asymptotex + y + a = 0 \,.It is symmetrical about y = x....
  
   by affine transformation
  Affine transformation
  In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
  
  .

External links

• Loy, Jim "Trisection of an Angle", Part VI