Folium of Descartes
Encyclopedia
In geometry
, the Folium of Descartes is an algebraic curve
defined by the equation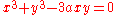
.
It forms a loop in the first quadrant with a double point at the origin and asymptote
.
It is symmetrical about
.
The name comes from the Latin
word folium which means "leaf
".
The curve was featured, along with a portrait of Descartes, on an Albanian stamp in 1966.
. Descartes challenged Fermat to find the tangent line to the curve at an arbitrary point since Fermat had recently discovered a method for finding tangent lines. Fermat solved the problem easily, something Descartes was unable to do. Since the invention of calculus, the slope of the tangent line can be found easily using implicit differentiation.
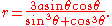
which can be plotted easily. Another technique is to write y = px and solve for x and y in terms of p. This yields the parametric equations:
.
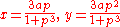We can see that the parameter is related to the position on the curve as follows:
by affine transformation
. To see this, start with the equation
,
and change variables to find the equation in a coordinate system rotated 45 degrees. This amounts to setting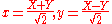
. In the 
plane the equation is
.
If we stretch the curve in the
direction by a factor of 
this becomes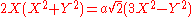
which is the equation of the trisectrix of Maclaurin.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Folium of Descartes is an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
defined by the equation
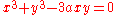.It forms a loop in the first quadrant with a double point at the origin and asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
.It is symmetrical about
.The name comes from the Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
word folium which means "leaf
Leaf
A leaf is an organ of a vascular plant, as defined in botanical terms, and in particular in plant morphology. Foliage is a mass noun that refers to leaves as a feature of plants....
".
The curve was featured, along with a portrait of Descartes, on an Albanian stamp in 1966.
History
The curve was first proposed by Descartes in 1638. Its claim to fame lies in an incident in the development of calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. Descartes challenged Fermat to find the tangent line to the curve at an arbitrary point since Fermat had recently discovered a method for finding tangent lines. Fermat solved the problem easily, something Descartes was unable to do. Since the invention of calculus, the slope of the tangent line can be found easily using implicit differentiation.
Graphing the curve
Since the equation is degree 3 in both x and y, and does not factor, it is difficult to solve for one of the variables. However, the equation in polar coordinates is: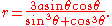which can be plotted easily. Another technique is to write y = px and solve for x and y in terms of p. This yields the parametric equations:
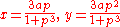.We can see that the parameter is related to the position on the curve as follows:
- p < -1 corresponds to the right, lower, "wing".
- -1 < p < 0 corresponds to the left, upper "wing".
- p > 0 corresponds to the loop of the curve.
Relationship to the trisectrix of MacLaurin
The folium of Descartes is related to the trisectrix of MaclaurinTrisectrix of Maclaurin
In geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the points of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the...
by affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
. To see this, start with the equation
,and change variables to find the equation in a coordinate system rotated 45 degrees. This amounts to setting
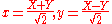. In the plane the equation is.If we stretch the curve in the
direction by a factor of this becomes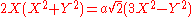which is the equation of the trisectrix of Maclaurin.