
Condensed Detachment
Encyclopedia
Condensed detachment is a method of finding the most general possible conclusion given two formal logical statements.
It was developed by the Irish logician Carew Meredith
in the 1950s and inspired by the work of Łukasiewicz.
"Given that implies
implies  , and given
, and given  , infer
, infer  ."
."
The condensed detachment goes a step further and says:
"Given that implies
implies  , and given an
, and given an  , use a unifier of
, use a unifier of 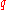 and
and  to make
to make  and
and  of the same form, then use a standard rule of detachment."
of the same form, then use a standard rule of detachment."
A substitution A that when applied to produces
produces  , and substitution B that when applied to
, and substitution B that when applied to  produces
produces  , are called the Unifiers of
, are called the Unifiers of 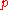 and
and  .
.
Various unifiers may produce expressions with varying numbers of free variables. Some possible unifying expressions are substitution instances of others. If one expression is a substitution instance of another (and not just a variable renaming), then that other is called "more general".
If the most general unifier is used in condensed detachment, then the logical result is the most general conclusion that can be made in the given inference with the given second expression. (And since any weaker inference you can get is a substitution instance of the most general one, nothing less than the most general unifier is ever used in practice.)
In some logics (such as standard PC) have a set of defining axioms with the "D-completeness" property. If a set of axioms is D-Complete, then any vaild theorems of the system can be generated by condensed detachment alone. Note that "D-completeness" is a property of an axiomatic basis for a system, not an intrinsic property of a logic system itself.
J.A.Kalman proved that any conclusion that can be generated by a sequence of uniform substitution and modus ponens
steps can either be generated by condensed detachment alone, or is a substitution instance of something that can be generated by condensed detachment alone.
This makes condensed detachment useful for any logic system that has modus ponens
and substitution, regardless of whether or not it is D-complete.
observed that it was only necessary to note which two statements were involved and that the condensed detachment can be used without any other notation required. This led to the "D-notation" for proofs
. This notation uses the "D" operator to mean condensed detachment, and takes 2 arguments, in a standard prefix notation string. For example, if you have four axioms a typical proof in D-notation might look like: DD12D34 which shows a condensed detachment step using the result of two prior condensed detachment steps, the first of which used axioms 1 and 2, and the second of which used axioms 3 and 4.
This notation, besides being used in some automated theorem provers, sometimes appears in catalogs of proofs
Condensed detachment's use of unification
predates the resolution
techniques of automated theorem proving
.
and uniform substitution.
At a Modus Ponens and substitution proof you have an infinite number of choices for what you can substitute for variables. This means that you have an infinite number of possible next steps. With condensed detachment there are only a finite number of possible next steps in a proof.
The D-notation for complete condensed detachment proofs allows easy description of proofs for cataloging and search. A typical complete 30 step proof is less than 60 characters long in D-notation (excluding the statement of the axioms.)
It was developed by the Irish logician Carew Meredith
Carew Meredith
Carew Arthur Meredith was an influential Irish logician, appointed to Trinity College, Dublin in 1947...
in the 1950s and inspired by the work of Łukasiewicz.
Informal description
A rule of detachment says:"Given that
 implies
implies  , and given
, and given  , infer
, infer  ."
."The condensed detachment goes a step further and says:
"Given that
 implies
implies  , and given an
, and given an  , use a unifier of
, use a unifier of 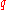 and
and  to make
to make  and
and  of the same form, then use a standard rule of detachment."
of the same form, then use a standard rule of detachment."A substitution A that when applied to
 produces
produces  , and substitution B that when applied to
, and substitution B that when applied to  produces
produces  , are called the Unifiers of
, are called the Unifiers of 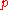 and
and  .
.Various unifiers may produce expressions with varying numbers of free variables. Some possible unifying expressions are substitution instances of others. If one expression is a substitution instance of another (and not just a variable renaming), then that other is called "more general".
If the most general unifier is used in condensed detachment, then the logical result is the most general conclusion that can be made in the given inference with the given second expression. (And since any weaker inference you can get is a substitution instance of the most general one, nothing less than the most general unifier is ever used in practice.)
In some logics (such as standard PC) have a set of defining axioms with the "D-completeness" property. If a set of axioms is D-Complete, then any vaild theorems of the system can be generated by condensed detachment alone. Note that "D-completeness" is a property of an axiomatic basis for a system, not an intrinsic property of a logic system itself.
J.A.Kalman proved that any conclusion that can be generated by a sequence of uniform substitution and modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
steps can either be generated by condensed detachment alone, or is a substitution instance of something that can be generated by condensed detachment alone.
This makes condensed detachment useful for any logic system that has modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
and substitution, regardless of whether or not it is D-complete.
D-notation
Since a given major premise and a given minor premise uniquely determine the conclusion (up to variable renaming), MeredithCarew Meredith
Carew Arthur Meredith was an influential Irish logician, appointed to Trinity College, Dublin in 1947...
observed that it was only necessary to note which two statements were involved and that the condensed detachment can be used without any other notation required. This led to the "D-notation" for proofs
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
. This notation uses the "D" operator to mean condensed detachment, and takes 2 arguments, in a standard prefix notation string. For example, if you have four axioms a typical proof in D-notation might look like: DD12D34 which shows a condensed detachment step using the result of two prior condensed detachment steps, the first of which used axioms 1 and 2, and the second of which used axioms 3 and 4.
This notation, besides being used in some automated theorem provers, sometimes appears in catalogs of proofs
Condensed detachment's use of unification
Unification
Unification, in computer science and logic, is an algorithmic process by which one attempts to solve the satisfiability problem. The goal of unification is to find a substitution which demonstrates that two seemingly different terms are in fact either identical or just equal...
predates the resolution
Resolution (logic)
In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation theorem-proving technique for sentences in propositional logic and first-order logic...
techniques of automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
.
Advantages
For automated theorem proving condensed detachment has a number of advantages over raw modus ponensModus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
and uniform substitution.
At a Modus Ponens and substitution proof you have an infinite number of choices for what you can substitute for variables. This means that you have an infinite number of possible next steps. With condensed detachment there are only a finite number of possible next steps in a proof.
The D-notation for complete condensed detachment proofs allows easy description of proofs for cataloging and search. A typical complete 30 step proof is less than 60 characters long in D-notation (excluding the statement of the axioms.)

