
Unification
Encyclopedia
Unification, in computer science
and logic
, is an algorithmic process by which one attempts to solve the satisfiability problem. The goal of unification is to find a substitution
which demonstrates that two seemingly different terms
are in fact either identical
or just equal. Unification is widely used in automated reasoning
, logic programming
and programming language type system
implementation.
Several kinds of unification are commonly studied: that for theories
without any equations (the empty theory) is referred to as syntactic unification: one wishes to show that (pairs of) terms are identical
. If one has a non-empty equational theory, then one is typically interested in showing the equality of (a pair of) terms; this is referred to as semantic unification. Since substitutions can be ordered into a partial order, unification can be understood as the procedure of finding a join on a lattice
.
Unification on ground terms is just the ground word problem
; because the ground word problem is undecidable
, so is unification.
The first formal investigation of unification can be attributed to John Alan Robinson
, who used first-order unification as a basic building block of his resolution
procedure for first-order logic, a great step forward in automated reasoning technology, as it eliminated one source of combinatorial explosion: searching for instantiation of terms.
defined as any expression that can be generated by a finite number of applications of the following rules:
E.g. x,y,a and b are terms that can be generated directly from the Basis rule;
f(a,x), g(b,y,x) are terms by a single application of the Induction rule to terms generated from the Basis;
f(a,f(a,x)) is a term generated by a second application of the Induction rule to terms we have already generated; and so on...
Often, for brevity, the constant symbols are regarded as function symbols taking zero arguments, the induction rule is relaxed to allow
terms with zero arguments
 ,
,
and a is regarded as syntactically equal to a: see first-order terms.
The distinction between constants (zero arity functions) and function symbols with arity greater than zero is often made to clearly distinguish Basis and Induction cases of terms for purposes of proofs.
Often mathematicians fix the arity (number of arguments) of a function symbol (see Signature
) while typically in syntactic unification problems
a function symbol may have any (finite) number of arguments, and possibly may have different numbers of arguments in different contexts.
e.g. f(f(a),f(x,y,z)) is a well formed term for unification problems.

where each mapping must be unique,
because mapping the same variable to two different terms would be ambiguous.
A substitution may be applied to a term u and is written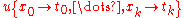 ,
,
which means (simultaneously) replace every occurrence of each variable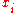 in the term
in the term  with the term
with the term  for
for 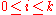 .
.
E.g.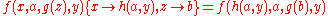
 .
.
To solve the problem, a substitution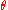 must be found so that the terms on LHS and RHS of each of the potential equalities become syntactically equivalent when the substitution is applied i.e.
must be found so that the terms on LHS and RHS of each of the potential equalities become syntactically equivalent when the substitution is applied i.e.  .
.
Such a substitution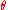 is called a unifier. Alternatively a unification problem might have no solution.
is called a unifier. Alternatively a unification problem might have no solution.
E.g. has a unifier
has a unifier 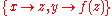 , because
, because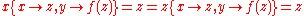 and
and 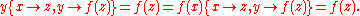
In theory, some pairs of input terms may have infinitely many unifiers. However, for most applications of unification, it is sufficient to consider a most general unifier (mgu). An mgu is useful because all other unifiers are instances of the mgu.
In particular, first-order unification is the syntactic unification of first-order terms (terms built from variable and function symbols). Higher-order unification, on the other hand, is the unification of higher-order terms (terms containing some higher-order variables).
The set of all syntactically equivalent terms is variously called the free theory (because it is a free object
), the empty theory (because the set of equational sentences
is empty), or the theory of uninterpreted function
s (because unification is done on uninterpreted terms
.)
The theoretical properties of a particular unification algorithm depend upon the variety of term used as input. First-order unification, for instance, is decidable, efficiently so, and all unifiable terms have (unique, up to variable renamings) most general unifiers. Higher-order unification, on the other hand, is generally undecidable and lacks most general unifiers, though Huet's higher-order unification algorithm seems to work sufficiently well in practice.
Aside from syntactic unification, another form of unification, called semantic unification (known also as equational-unification, E-unification) is also widely used. The key difference between the two notions of unification is how two unified terms should be considered 'equal'. Syntactic unification attempts to find a substitution making the two input terms structurally identical. However, semantic unification attempts to make the two input terms equal modulo some equational theory. Some particularly important equational theories have been widely studied in the literature. For instance, AC-unification is the unification of terms modulo associativity and commutativity.
Unification is a significant tool in computer science. First-order unification is especially widely used in logic programming
, programming language type system
design, especially in type inferencing algorithms based on the Hindley-Milner type system, and automated reasoning
. Higher-order unification is also widely used in proof assistants, for example Isabelle and Twelf
, and restricted forms of higher-order unification (higher-order pattern unification) are used in some programming language implementations, such as lambdaProlog, as higher-order patterns are expressive, yet their associated unification procedure retains theoretical properties closer to first-order unification. Semantic unification is widely used in SMT solvers and term rewriting algorithms.
.
Where subst(U,p) means the result of applying substitution U on the sentence p. Then U is called a unifier for p and q. The unification of p and q is the result of applying U to both of them.
Let L be a set of sentences, for example, L = {p,q}. A unifier U is called a most general unifier for L if, for all unifiers U' of L, there exists a substitution s such that applying s to the result of applying U to L gives the same result as applying U' to L:
, best known through the language Prolog
. It represents the mechanism of binding the contents of variables and can be viewed as a kind of one-time assignment. In Prolog, this operation is denoted by the equality symbol =, but is also done when instantiating variables (see below). It is also used in other languages by the use of the equality symbol =, but also in conjunction with many operations including +, -, *, /. Type inference
algorithms are typically based on unification.
In Prolog:
. On one hand, the programmer does not need to provide type information for every function, on the other hand it is used to detect typing errors. The Haskell expression1:['a','b','c'] is not correctly typed, because the list construction function ":" is of type a->[a]->[a] and for the first argument "1" the polymorphic type variable "a" has to denote the type Int whereas "['a','b','c'] " is of type [Char] , but "a" cannot be both Char and Int at the same time.
Like for prolog an algorithm for type inference can be given:
Due to its declarative nature, the order in a sequence of unifications is (usually) unimportant.
Note that in the terminology of first-order logic
, an atom is a basic proposition and is unified similarly to a Prolog term.
, Gérard Huet
gave a semi-decidable (pre-)unification algorithm that allows a systematic search of the space of unifiers (generalizing the unification algorithm of Martelli-Montanari with rules for terms containing higher-order variables. Huet and Gilles Dowek have written articles surveying this topic.
Dale Miller has described what is now called higher-order pattern unification. This subset of higher-order unification is decidable and solvable unification problems have most-general unifiers. Many computer systems that contain higher-order unification, such as the higher-order logic programming languages λProlog and Twelf
, often implement only the pattern fragment and not full higher-order unification.
In computational linguistics, one of the most influential theories of ellipsis
is that ellipses are represented by free variables whose values are then determined using Higher-Order Unification (HOU). For instance, the semantic representation of "Jon likes Mary and Peter does too" is like(j; m)R(p) and the value of R (the semantic representation of the ellipsis) is determined by the equation like(j; m) = R(j). The process of solving such equations is called Higher-Order Unification.
In maths the convention is to use lower case letters at the end of the alphabet as variable names (e.g. x,y,z); letters f,g,h as function symbols, and letters a,b,c as constants, and constants are often regarded as functions that take no arguments; logical "and" is represented by & or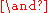
 consisting of a finite multi-set of potential equations
consisting of a finite multi-set of potential equations
on terms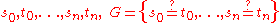 ,
,
the algorithm applies term rewriting rules to transform the multi-set of
potential equations to an equivalent multi-set of equations of the form
 where
where 
are unique variables (appearing exactly once on the LHS of one equation, and nowhere else). A multi-set of this form can be read as a substitution.
If there is no solution the algorithm terminates with .
.
The set of variables in a term is written as
is written as 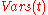 , and the set of variables in all terms on LHS or RHS of potential equations in a problem
, and the set of variables in all terms on LHS or RHS of potential equations in a problem  is similarly written as
is similarly written as  . The operation of substituting all occurrences of variable
. The operation of substituting all occurrences of variable  in problem
in problem  with term
with term  is denoted
is denoted 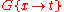 . For brevity constant symbols are regarded as function symbols having zero arguments.
. For brevity constant symbols are regarded as function symbols having zero arguments.
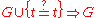
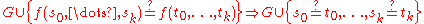
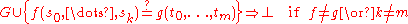
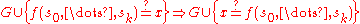

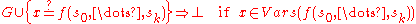
where NUVN is the number of non-unique variables, NLHS is the number of function symbols and constants
on the LHS of potential equations, and EQN is the number of equations.
The application of these rewrite rules in any order terminates because NUVN remains the same or is reduced by each rewrite.
Where NUVN remains the same, NLHS remains the same or is reduced by each rewrite.
Where NUVN remains the same and NLHS remains the same, EQN is reduced by each rewrite.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, is an algorithmic process by which one attempts to solve the satisfiability problem. The goal of unification is to find a substitution
Substitution (logic)
Substitution is a fundamental concept in logic. Substitution is a syntactic transformation on strings of symbols of a formal language.In propositional logic, a substitution instance of a propositional formula is a second formula obtained by replacing symbols of the original formula by other formulas...
which demonstrates that two seemingly different terms
Term (logic)
In mathematical logic, universal algebra, and rewriting systems, terms are expressions which can be obtained from constant symbols, variables and function symbols...
are in fact either identical
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
or just equal. Unification is widely used in automated reasoning
Automated reasoning
Automated reasoning is an area of computer science dedicated to understand different aspects of reasoning. The study in automated reasoning helps produce software which allows computers to reason completely, or nearly completely, automatically...
, logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
and programming language type system
Type system
A type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur...
implementation.
Several kinds of unification are commonly studied: that for theories
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
without any equations (the empty theory) is referred to as syntactic unification: one wishes to show that (pairs of) terms are identical
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
. If one has a non-empty equational theory, then one is typically interested in showing the equality of (a pair of) terms; this is referred to as semantic unification. Since substitutions can be ordered into a partial order, unification can be understood as the procedure of finding a join on a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
.
Unification on ground terms is just the ground word problem
Word problem (mathematics)
In mathematics and computer science, a word problem for a set S with respect to a system of finite encodings of its elements is the algorithmic problem of deciding whether two given representatives represent the same element of the set...
; because the ground word problem is undecidable
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
, so is unification.
The first formal investigation of unification can be attributed to John Alan Robinson
J. Alan Robinson
John Alan Robinson is a philosopher , mathematician and computer scientist. He is University Professor Emeritus at Syracuse University, United States....
, who used first-order unification as a basic building block of his resolution
Resolution (logic)
In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation theorem-proving technique for sentences in propositional logic and first-order logic...
procedure for first-order logic, a great step forward in automated reasoning technology, as it eliminated one source of combinatorial explosion: searching for instantiation of terms.
First-order terms
Given a set of variable symbols X = {x,y,z,...}, a set of distinct constant symbols C = {a,b,c,...}, and a set of distinct function symbols F = {f,g,h,...}, a term isdefined as any expression that can be generated by a finite number of applications of the following rules:
- Basis: any variable
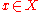 , and also any constant
, and also any constant  is a term
is a term - Induction: if
 are terms then
are terms then  is term for finite k, 0 < k.
is term for finite k, 0 < k.
E.g. x,y,a and b are terms that can be generated directly from the Basis rule;
f(a,x), g(b,y,x) are terms by a single application of the Induction rule to terms generated from the Basis;
f(a,f(a,x)) is a term generated by a second application of the Induction rule to terms we have already generated; and so on...
Often, for brevity, the constant symbols are regarded as function symbols taking zero arguments, the induction rule is relaxed to allow
terms with zero arguments
 ,
,and a is regarded as syntactically equal to a: see first-order terms.
The distinction between constants (zero arity functions) and function symbols with arity greater than zero is often made to clearly distinguish Basis and Induction cases of terms for purposes of proofs.
Often mathematicians fix the arity (number of arguments) of a function symbol (see Signature
Signature
A signature is a handwritten depiction of someone's name, nickname, or even a simple "X" that a person writes on documents as a proof of identity and intent. The writer of a signature is a signatory. Similar to a handwritten signature, a signature work describes the work as readily identifying...
) while typically in syntactic unification problems
a function symbol may have any (finite) number of arguments, and possibly may have different numbers of arguments in different contexts.
e.g. f(f(a),f(x,y,z)) is a well formed term for unification problems.
Substitution
A substitution is defined as a finite set of mappings from variables to terms
where each mapping must be unique,
because mapping the same variable to two different terms would be ambiguous.
A substitution may be applied to a term u and is written
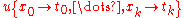 ,
,which means (simultaneously) replace every occurrence of each variable
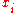 in the term
in the term  with the term
with the term  for
for 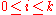 .
.E.g.
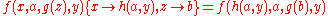
Syntactic unification problem on first-order terms
A syntactic unification problem on first-order terms is a conjunction of a finite number of potential equations on terms .
.To solve the problem, a substitution
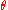 must be found so that the terms on LHS and RHS of each of the potential equalities become syntactically equivalent when the substitution is applied i.e.
must be found so that the terms on LHS and RHS of each of the potential equalities become syntactically equivalent when the substitution is applied i.e.  .
.Such a substitution
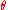 is called a unifier. Alternatively a unification problem might have no solution.
is called a unifier. Alternatively a unification problem might have no solution.E.g.
 has a unifier
has a unifier 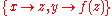 , because
, because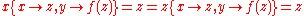 and
and 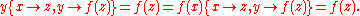
Occurs check
If there is ever an attempt to unify a variable x with a term with a function symbol containing x as a strict subterm x=f(...,x,...) then x would have to be an infinite term, which contradicts the strict definition of terms that requires a finite number of applications of the induction rule. e.g x=f(x) does not represent a strictly valid term.Informal overview
Given two input terms s and t, (syntactic) unification is the process which attempts to find a substitution that structurally identifies s and t. If such a substitution exists, we call this substitution a unifier of s and t.In theory, some pairs of input terms may have infinitely many unifiers. However, for most applications of unification, it is sufficient to consider a most general unifier (mgu). An mgu is useful because all other unifiers are instances of the mgu.
In particular, first-order unification is the syntactic unification of first-order terms (terms built from variable and function symbols). Higher-order unification, on the other hand, is the unification of higher-order terms (terms containing some higher-order variables).
The set of all syntactically equivalent terms is variously called the free theory (because it is a free object
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
), the empty theory (because the set of equational sentences
Sentence (mathematical logic)
In mathematical logic, a sentence of a predicate logic is a boolean-valued well formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that may be true or false...
is empty), or the theory of uninterpreted function
Uninterpreted function
In mathematical logic, an uninterpreted function or function symbol is one that has no other property than its name and arity. Function symbols are used, together with constants and variables, to form terms....
s (because unification is done on uninterpreted terms
Term (logic)
In mathematical logic, universal algebra, and rewriting systems, terms are expressions which can be obtained from constant symbols, variables and function symbols...
.)
The theoretical properties of a particular unification algorithm depend upon the variety of term used as input. First-order unification, for instance, is decidable, efficiently so, and all unifiable terms have (unique, up to variable renamings) most general unifiers. Higher-order unification, on the other hand, is generally undecidable and lacks most general unifiers, though Huet's higher-order unification algorithm seems to work sufficiently well in practice.
Aside from syntactic unification, another form of unification, called semantic unification (known also as equational-unification, E-unification) is also widely used. The key difference between the two notions of unification is how two unified terms should be considered 'equal'. Syntactic unification attempts to find a substitution making the two input terms structurally identical. However, semantic unification attempts to make the two input terms equal modulo some equational theory. Some particularly important equational theories have been widely studied in the literature. For instance, AC-unification is the unification of terms modulo associativity and commutativity.
Unification is a significant tool in computer science. First-order unification is especially widely used in logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
, programming language type system
Type system
A type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur...
design, especially in type inferencing algorithms based on the Hindley-Milner type system, and automated reasoning
Automated reasoning
Automated reasoning is an area of computer science dedicated to understand different aspects of reasoning. The study in automated reasoning helps produce software which allows computers to reason completely, or nearly completely, automatically...
. Higher-order unification is also widely used in proof assistants, for example Isabelle and Twelf
Twelf
Twelf is an implementation of the logical framework LF. It is used for logic programming and for the formalization of programming language theory.-Introduction:...
, and restricted forms of higher-order unification (higher-order pattern unification) are used in some programming language implementations, such as lambdaProlog, as higher-order patterns are expressive, yet their associated unification procedure retains theoretical properties closer to first-order unification. Semantic unification is widely used in SMT solvers and term rewriting algorithms.
Definition of unification for first-order logic
Let p and q be sentences in first-order logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
.
- UNIFY(p,q) = U where subst(U,p) = subst(U,q)
Where subst(U,p) means the result of applying substitution U on the sentence p. Then U is called a unifier for p and q. The unification of p and q is the result of applying U to both of them.
Let L be a set of sentences, for example, L = {p,q}. A unifier U is called a most general unifier for L if, for all unifiers U' of L, there exists a substitution s such that applying s to the result of applying U to L gives the same result as applying U' to L:
- subst(U',L) = subst(s,subst(U,L)).
Unification in logic programming
The concept of unification is one of the main ideas behind logic programmingLogic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
, best known through the language Prolog
Prolog
Prolog is a general purpose logic programming language associated with artificial intelligence and computational linguistics.Prolog has its roots in first-order logic, a formal logic, and unlike many other programming languages, Prolog is declarative: the program logic is expressed in terms of...
. It represents the mechanism of binding the contents of variables and can be viewed as a kind of one-time assignment. In Prolog, this operation is denoted by the equality symbol =, but is also done when instantiating variables (see below). It is also used in other languages by the use of the equality symbol =, but also in conjunction with many operations including +, -, *, /. Type inference
Type inference
Type inference refers to the automatic deduction of the type of an expression in a programming language. If some, but not all, type annotations are already present it is referred to as type reconstruction....
algorithms are typically based on unification.
In Prolog:
- A variableVariable (programming)In computer programming, a variable is a symbolic name given to some known or unknown quantity or information, for the purpose of allowing the name to be used independently of the information it represents...
which is uninstantiated—i.e. no previous unifications were performed on it—can be unified with an atom, a term, or another uninstantiated variable, thus effectively becoming its alias. In many modern Prolog dialects and in first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, a variable cannot be unified with a term that contains it; this is the so called occurs checkOccurs checkIn computer science, the occurs check is a part of algorithms forsyntactic unification. It causes unification of a logic variable V and a structure S to fail if S contains V....
. - Two atoms can only be unified if they are identical.
- Similarly, a term can be unified with another term if the top function symbols and aritiesArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
of the terms are identical and if the parameters can be unified simultaneously. Note that this is a recursive behavior.
Type inference
Unification is used during type inference, for instance in the functional programming language Haskell (programming language)Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
. On one hand, the programmer does not need to provide type information for every function, on the other hand it is used to detect typing errors. The Haskell expression
Like for prolog an algorithm for type inference can be given:
- Any type variable unifies with any type expression, and is instantiated to that expression. A specific theory might restrict this rule with an occurs check.
- Two type constants unify only if they are the same type.
- Two type constructions unify only if they are applications of the same type constructor and all of their component types recursively unify.
Due to its declarative nature, the order in a sequence of unifications is (usually) unimportant.
Note that in the terminology of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, an atom is a basic proposition and is unified similarly to a Prolog term.
Higher-order unification
Many applications require one to consider the unification of typed lambda-terms instead of first-order terms. Such unification is often called higher-order unification. A well studied branch of higher-order unification is the problem of unifying simply typed lambda terms modulo the equality determined by αβη conversions. Such unification problems do not have most general unifiers. While higher-order unification is undecidableUndecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
, Gérard Huet
Gérard Huet
Gérard Pierre Huet is a French computer scientist.- Biography :Gérard Huet graduated from the Université Denis Diderot , Case Western Reserve University, and the Université de Paris....
gave a semi-decidable (pre-)unification algorithm that allows a systematic search of the space of unifiers (generalizing the unification algorithm of Martelli-Montanari with rules for terms containing higher-order variables. Huet and Gilles Dowek have written articles surveying this topic.
Dale Miller has described what is now called higher-order pattern unification. This subset of higher-order unification is decidable and solvable unification problems have most-general unifiers. Many computer systems that contain higher-order unification, such as the higher-order logic programming languages λProlog and Twelf
Twelf
Twelf is an implementation of the logical framework LF. It is used for logic programming and for the formalization of programming language theory.-Introduction:...
, often implement only the pattern fragment and not full higher-order unification.
In computational linguistics, one of the most influential theories of ellipsis
Elliptical construction
In linguistics, ellipsis or elliptical construction refers to the omission from a clause of one or more words that would otherwise be required by the remaining elements.-Overview:...
is that ellipses are represented by free variables whose values are then determined using Higher-Order Unification (HOU). For instance, the semantic representation of "Jon likes Mary and Peter does too" is like(j; m)R(p) and the value of R (the semantic representation of the ellipsis) is determined by the equation like(j; m) = R(j). The process of solving such equations is called Higher-Order Unification.
Examples of syntactic unification of first-order terms
In the Prolog syntactical convention a symbol starting with an upper case letter is a variable name; a symbol that starts with a lowercase letter is a function symbol; the comma is used as the logical and operator.In maths the convention is to use lower case letters at the end of the alphabet as variable names (e.g. x,y,z); letters f,g,h as function symbols, and letters a,b,c as constants, and constants are often regarded as functions that take no arguments; logical "and" is represented by & or
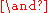
| Prolog Notation | Maths Notation | Unifying Substitution | Explanation |
|---|---|---|---|
| a = a | a = a | Succeeds. (tautology Tautology (logic) In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense... ) |
|
| a = b | a = b | fail | a and b do not match |
| X = X | x = x | Succeeds. (tautology Tautology (logic) In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense... ) |
|
| a = X | a = x |  |
x is unified with the constant a |
| X = Y | x = y |  |
x and y are aliased |
| f(a,X) = f(a,b) | f(a,x) = f(a,b) |  |
function and constant symbols match, x is unified with the constant b |
| f(a) = g(a) | f(a) = g(a) | fail | f and g do not match |
| f(X) = f(Y) | f(x) = f(y) |  |
x and y are aliased |
| f(X) = g(Y) | f(x) = g(y) | fail | f and g do not match |
| f(X) = f(Y,Z) | f(x) = f(y,z) | fail | Fails. The terms have different arity |
| f(g(X)) = f(Y) | f(g(x)) = f(y) | 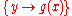 |
Unifies y with the term g(x) |
| f(g(X),X) = f(Y,a) | f(g(x),x) = f(y,a) | 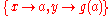 |
Unifies x with constant a, and y with the term g(a) |
| X = f(X) | x = f(x) | should fail | Fails in strict first-order logic and many modern Prolog dialects (enforced by the occurs check Occurs check In computer science, the occurs check is a part of algorithms forsyntactic unification. It causes unification of a logic variable V and a structure S to fail if S contains V.... ). Succeeds in traditional Prolog, unifying x with infinite expression x=f(f(f(f(...)))) which is not strictly a term. |
| X = Y, Y = a | x = y & y = a | 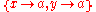 |
Both x and y are unified with the constant a |
| a = Y, X = Y | a = y & x = y | 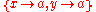 |
As above (unification is symmetric, and transitive) |
| X = a, b = X | x = a & b = x | fail | Fails. a and b do not match, so x can't be unified with both |
A Unification Algorithm
Given a unification problem consisting of a finite multi-set of potential equations
consisting of a finite multi-set of potential equationson terms
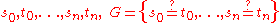 ,
,the algorithm applies term rewriting rules to transform the multi-set of
potential equations to an equivalent multi-set of equations of the form
 where
where 
are unique variables (appearing exactly once on the LHS of one equation, and nowhere else). A multi-set of this form can be read as a substitution.
If there is no solution the algorithm terminates with
 .
.The set of variables in a term
 is written as
is written as 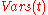 , and the set of variables in all terms on LHS or RHS of potential equations in a problem
, and the set of variables in all terms on LHS or RHS of potential equations in a problem  is similarly written as
is similarly written as  . The operation of substituting all occurrences of variable
. The operation of substituting all occurrences of variable  in problem
in problem  with term
with term  is denoted
is denoted 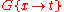 . For brevity constant symbols are regarded as function symbols having zero arguments.
. For brevity constant symbols are regarded as function symbols having zero arguments.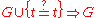
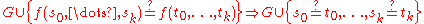
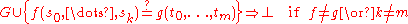
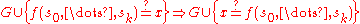

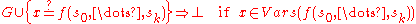
Proof of Termination
For the proof of termination consider a 3-tuplewhere NUVN is the number of non-unique variables, NLHS is the number of function symbols and constants
on the LHS of potential equations, and EQN is the number of equations.
The application of these rewrite rules in any order terminates because NUVN remains the same or is reduced by each rewrite.
Where NUVN remains the same, NLHS remains the same or is reduced by each rewrite.
Where NUVN remains the same and NLHS remains the same, EQN is reduced by each rewrite.
See also
- Admissible ruleAdmissible ruleIn logic, a rule of inference is admissible in a formal system if the set of theorems of the system does not change when that rule is added to the existing rules of the system. In other words, every formula that can be derived using that rule is already derivable without that rule, so, in a sense,...
- Semantic UnificationSemantic unificationSemantic unification, in philosophy, linguistics, and computer science, is the process of unifying lexically different concept representations that are judged to have the same semantic content ....
- Explicit substitutionExplicit substitutionIn computer science, lambda calculi are said to have explicit substitutions if they pay special attention to the formalization of the process of substitution. This is in contrast to the standard lambda calculus where substitutions are performed by beta reductions in an implicit manner which is not...
in lambda calculusLambda calculusIn mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...

