
Conditional mutual information
Encyclopedia
In probability theory
, and in particular, information theory
, the conditional mutual information is, in its most basic form, the expected value
of the mutual information
of two random variables given the value of a third.

 and
and 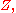 we define
we define
where the marginal, joint, and/or conditional probability mass function
s are denoted by with the appropriate subscript. This can be simplified as
with the appropriate subscript. This can be simplified as
Alternatively, we may write
Conditional mutual information can also be rewritten to show its relationship to mutual information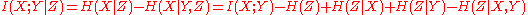
Conditioning on a third random variable may either increase or decrease the mutual information: that is, the difference , called the interaction information
, called the interaction information
, may be positive, negative, or zero, but it is always true that
for discrete, jointly distributed random variables X, Y, Z. This result has been used as a basic building block for proving other inequalities in information theory
, in particular, those known as Shannon-type inequalities.
Like mutual information, conditional mutual information can be expressed as a Kullback-Leibler divergence:

Or as an expected value of simpler Kullback-Leibler divergences: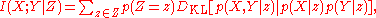
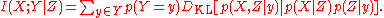
. (See also.)
Let be a probability space
be a probability space
, and let the random variables X, Y, and Z each be defined as a Borel-measurable function from to some state space endowed with a topological structure.
to some state space endowed with a topological structure.
Consider the Borel measure (on the σ-algebra generated by the open sets) in the state space of each random variable defined by assigning each Borel set the -measure of its preimage in
-measure of its preimage in 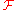 . This is called the pushforward measure
. This is called the pushforward measure
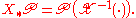 The support of a random variable is defined to be the topological support
The support of a random variable is defined to be the topological support
of this measure, i.e.
Now we can formally define the conditional probability measure given the value of one (or, via the product topology
, more) of the random variables. Let be a measurable subset of
be a measurable subset of  (i.e.
(i.e.  ) and let
) and let 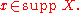 Then, using the disintegration theorem
Then, using the disintegration theorem
:
where the limit is taken over the open neighborhoods of
of  , as they are allowed to become arbitrarily smaller with respect to set inclusion
, as they are allowed to become arbitrarily smaller with respect to set inclusion
.
Finally we can define the conditional mutual information via Lebesgue integration
: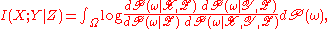
where the integrand is the logarithm of a Radon–Nikodym derivative involving some of the conditional probability measures we have just defined.
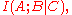

 and
and  need not necessarily be restricted to representing individual random variables, but could also represent the joint distribution of any collection of random variables defined on the same probability space
need not necessarily be restricted to representing individual random variables, but could also represent the joint distribution of any collection of random variables defined on the same probability space
. As is common in probability theory
, we may use the comma to denote such a joint distribution, e.g. Hence the use of the semicolon (or occasionally a colon or even a wedge
Hence the use of the semicolon (or occasionally a colon or even a wedge  ) to separate the principal arguments of the mutual information symbol. (No such distinction is necessary in the symbol for joint entropy, since the joint entropy of any number of random variables is the same as the entropy of their joint distribution.)
) to separate the principal arguments of the mutual information symbol. (No such distinction is necessary in the symbol for joint entropy, since the joint entropy of any number of random variables is the same as the entropy of their joint distribution.)
in the context of information diagram
s. In this sense we define the multivariate mutual information as follows:
where
This definition is identical to that of interaction information
except for a change in sign in the case of an odd number of random variables. A complication is that this multivariate mutual information (as well as the interaction information) can be positive, negative, or zero, which makes this quantity difficult to interpret intuitively. In fact, for n random variables, there are degrees of freedom for how they might be correlated in an information-theoretic sense, corresponding to each non-empty subset of these variables. These degrees of freedom are bounded by various Shannon- and non-Shannon-type inequalities in information theory
degrees of freedom for how they might be correlated in an information-theoretic sense, corresponding to each non-empty subset of these variables. These degrees of freedom are bounded by various Shannon- and non-Shannon-type inequalities in information theory
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, and in particular, information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, the conditional mutual information is, in its most basic form, the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
of two random variables given the value of a third.
Definition
For discrete random variables
 and
and 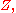 we define
we define
where the marginal, joint, and/or conditional probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
s are denoted by
 with the appropriate subscript. This can be simplified as
with the appropriate subscript. This can be simplified as
Alternatively, we may write

Conditional mutual information can also be rewritten to show its relationship to mutual information
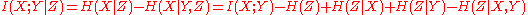
Conditioning on a third random variable may either increase or decrease the mutual information: that is, the difference
 , called the interaction information
, called the interaction informationInteraction information
The interaction information or co-information is one of several generalizations of the mutual information, and expresses the amount information bound up in a set of variables, beyond that which is present in any subset of those variables...
, may be positive, negative, or zero, but it is always true that

for discrete, jointly distributed random variables X, Y, Z. This result has been used as a basic building block for proving other inequalities in information theory
Inequalities in information theory
Inequalities are very important in the study of information theory. There are a number of different contexts in which these inequalities appear.-Shannon-type inequalities:...
, in particular, those known as Shannon-type inequalities.
Like mutual information, conditional mutual information can be expressed as a Kullback-Leibler divergence:

Or as an expected value of simpler Kullback-Leibler divergences:
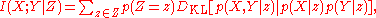
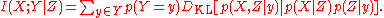
More general definition
A more general definition of conditional mutual information, applicable to random variables with continuous or other arbitrary distributions, will depend on the concept of regular conditional probabilityRegular conditional probability
Regular conditional probability is a concept that has developed to overcome certain difficulties in formally defining conditional probabilities for continuous probability distributions...
. (See also.)
Let
 be a probability space
be a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, and let the random variables X, Y, and Z each be defined as a Borel-measurable function from
 to some state space endowed with a topological structure.
to some state space endowed with a topological structure.Consider the Borel measure (on the σ-algebra generated by the open sets) in the state space of each random variable defined by assigning each Borel set the
 -measure of its preimage in
-measure of its preimage in 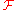 . This is called the pushforward measure
. This is called the pushforward measurePushforward measure
In measure theory, a pushforward measure is obtained by transferring a measure from one measurable space to another using a measurable function.-Definition:...
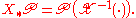 The support of a random variable is defined to be the topological support
The support of a random variable is defined to be the topological supportSupport (measure theory)
In mathematics, the support of a measure μ on a measurable topological space is a precise notion of where in the space X the measure "lives"...
of this measure, i.e.

Now we can formally define the conditional probability measure given the value of one (or, via the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
, more) of the random variables. Let
 be a measurable subset of
be a measurable subset of  (i.e.
(i.e.  ) and let
) and let 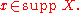 Then, using the disintegration theorem
Then, using the disintegration theoremDisintegration theorem
In mathematics, the disintegration theorem is a result in measure theory and probability theory. It rigorously defines the idea of a non-trivial "restriction" of a measure to a measure zero subset of the measure space in question. It is related to the existence of conditional probability measures...
:

where the limit is taken over the open neighborhoods
 of
of  , as they are allowed to become arbitrarily smaller with respect to set inclusion
, as they are allowed to become arbitrarily smaller with respect to set inclusionSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
.
Finally we can define the conditional mutual information via Lebesgue integration
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
:
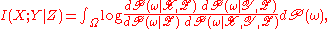
where the integrand is the logarithm of a Radon–Nikodym derivative involving some of the conditional probability measures we have just defined.
Note on notation
In an expression such as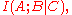

 and
and  need not necessarily be restricted to representing individual random variables, but could also represent the joint distribution of any collection of random variables defined on the same probability space
need not necessarily be restricted to representing individual random variables, but could also represent the joint distribution of any collection of random variables defined on the same probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
. As is common in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, we may use the comma to denote such a joint distribution, e.g.
 Hence the use of the semicolon (or occasionally a colon or even a wedge
Hence the use of the semicolon (or occasionally a colon or even a wedge  ) to separate the principal arguments of the mutual information symbol. (No such distinction is necessary in the symbol for joint entropy, since the joint entropy of any number of random variables is the same as the entropy of their joint distribution.)
) to separate the principal arguments of the mutual information symbol. (No such distinction is necessary in the symbol for joint entropy, since the joint entropy of any number of random variables is the same as the entropy of their joint distribution.)Multivariate mutual information
The conditional mutual information can be used to inductively define a multivariate mutual information in a set- or measure-theoretic senseInformation theory and measure theory
- Measures in information theory :Many of the formulas in information theory have separate versions for continuous and discrete cases, i.e. integrals for the continuous case and sums for the discrete case. These versions can often be generalized using measure theory...
in the context of information diagram
Information diagram
An information diagram is a type of Venn diagram used in information theory to illustrate relationships among Shannon's basic measures of information: entropy, joint entropy, conditional entropy and mutual information...
s. In this sense we define the multivariate mutual information as follows:

where

This definition is identical to that of interaction information
Interaction information
The interaction information or co-information is one of several generalizations of the mutual information, and expresses the amount information bound up in a set of variables, beyond that which is present in any subset of those variables...
except for a change in sign in the case of an odd number of random variables. A complication is that this multivariate mutual information (as well as the interaction information) can be positive, negative, or zero, which makes this quantity difficult to interpret intuitively. In fact, for n random variables, there are
 degrees of freedom for how they might be correlated in an information-theoretic sense, corresponding to each non-empty subset of these variables. These degrees of freedom are bounded by various Shannon- and non-Shannon-type inequalities in information theory
degrees of freedom for how they might be correlated in an information-theoretic sense, corresponding to each non-empty subset of these variables. These degrees of freedom are bounded by various Shannon- and non-Shannon-type inequalities in information theoryInequalities in information theory
Inequalities are very important in the study of information theory. There are a number of different contexts in which these inequalities appear.-Shannon-type inequalities:...
.

