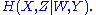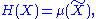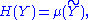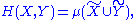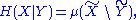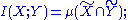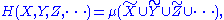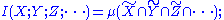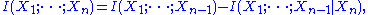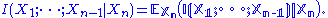
Information theory and measure theory
Encyclopedia
Measures in information theory
Many of the formulas in information theory have separate versions for continuous and discrete cases, i.e. integralIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s for the continuous case and sums for the discrete case. These versions can often be generalized using measure theory. For discrete random variables, probability mass functions can be considered density functions with respect to the counting measure, thus requiring only basic discrete mathematics
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
for what can be considered, in a measure theory context, integration. Because the same integration expression is used for the continuous case, which uses basic calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, the same concepts and expressions can be used for both discrete and continuous cases. Consider the formula for the differential entropy
Differential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
of a continuous random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
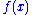 :
: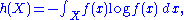
This can usually be taken to be
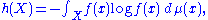
where μ is the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. But if instead, X is discrete, f is a probability mass function, and ν is the counting measure
Counting measure
In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
, we can write:
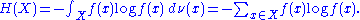
The integral expression and the general concept is identical to the continuous case; the only difference is the measure used. In both cases the probability density function f is the Radon–Nikodym derivative
Radon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
of the probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
with respect to the measure against which the integral is taken.
If
 is the probability measure on X, then the integral can also be taken directly with respect to
is the probability measure on X, then the integral can also be taken directly with respect to 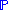 :
: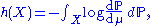
If instead of the underlying measure μ we take another probability measure
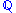 , we are led to the Kullback–Leibler divergence
, we are led to the Kullback–Leibler divergenceKullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
: let
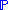 and
and 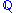 be probability measures over the same space. Then if
be probability measures over the same space. Then if 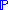 is absolutely continuous
is absolutely continuousAbsolute continuity
In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
with respect to
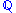 , written
, written 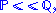 the Radon–Nikodym derivative
the Radon–Nikodym derivativeRadon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
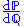 exists and the Kullback–Leibler divergence can be expressed in its full generality:
exists and the Kullback–Leibler divergence can be expressed in its full generality: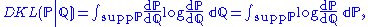
where the integral runs over the support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of
 Note that we have dropped the negative sign: the Kullback–Leibler divergence is always non-negative due to Gibbs' inequality
Note that we have dropped the negative sign: the Kullback–Leibler divergence is always non-negative due to Gibbs' inequalityGibbs' inequality
In information theory, Gibbs' inequality is a statement about the mathematical entropy of a discrete probability distribution. Several other bounds on the entropy of probability distributions are derived from Gibbs' inequality, including Fano's inequality....
.
Entropy as a "measure"
There is an analogy between ShannonClaude Elwood Shannon
Claude Elwood Shannon was an American mathematician, electronic engineer, and cryptographer known as "the father of information theory"....
's basic "measures
Quantities of information
The mathematical theory of information is based on probability theory and statistics, and measures information with several quantities of information. The choice of logarithmic base in the following formulae determines the unit of information entropy that is used. The most common unit of...
" of the information
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
content of random variables and a measure over sets. Namely the joint entropy, conditional entropy
Conditional entropy
In information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
, and mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
can be considered as the measure of a set union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
, set difference, and set intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
, respectively (Reza pp. 106-108).
If we associate the existence of abstract sets
 and
and  to arbitrary discrete
to arbitrary discreteDiscrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X and Y, somehow representing the information
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
borne by X and Y, respectively, such that:
-
 whenever X and Y are unconditionally independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
whenever X and Y are unconditionally independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, and -
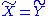 whenever X and Y are such that either one is completely determined by the other (i.e. by a bijection);
whenever X and Y are such that either one is completely determined by the other (i.e. by a bijection);
where
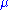 is a signed measure
is a signed measureSigned measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
over these sets, and we set:
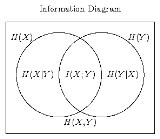
we find that Shannon
Claude Elwood Shannon
Claude Elwood Shannon was an American mathematician, electronic engineer, and cryptographer known as "the father of information theory"....
's "measure" of information content satisfies all the postulates and basic properties of a formal measure over sets, as commonly illustrated in an information diagram
Information diagram
An information diagram is a type of Venn diagram used in information theory to illustrate relationships among Shannon's basic measures of information: entropy, joint entropy, conditional entropy and mutual information...
. This can be a handy mnemonic device in some situations, e.g.
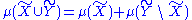 |
|
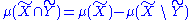 |
Because the entropy, joint entropy, conditional entropy, and bivariate mutual information of discrete random variables are all nonnegative, many basic inequalities in information theory
Inequalities in information theory
Inequalities are very important in the study of information theory. There are a number of different contexts in which these inequalities appear.-Shannon-type inequalities:...
(among no more than two random variables) can be derived from this formulation by considering the measure μ to be nonnegative.
Multivariate mutual information
Certain extensions to the definitions of Shannon's basic measures of information are necessary to deal with the σ-algebraSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
generated by the sets that would be associated to three or more arbitrary random variables. (See Reza pp. 106-108 for an informal but rather complete discussion.) Namely
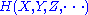 needs to be defined in the obvious way as the entropy of a joint distribution, and a multivariate mutual information
needs to be defined in the obvious way as the entropy of a joint distribution, and a multivariate mutual informationMutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
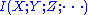 defined in a suitable manner so that we can set:
defined in a suitable manner so that we can set:in order to define the (signed) measure over the whole σ-algebra. There is no single universally accepted definition for the mutivariate mutual information, but the one that corresponds here to the measure of a set intersection is due to Fano (Srinivasa). The definition is recursive. As a base case the mutual information of a single random variable is defined to be its entropy:
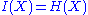 . Then for
. Then for  we set
we set
where the conditional mutual information
Conditional mutual information
In probability theory, and in particular, information theory, the conditional mutual information is, in its most basic form, the expected value of the mutual information of two random variables given the value of a third.-Definition:...
is defined as
The first step in the recursion yields Shannon's definition
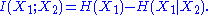 It is interesting to note that the mutual information (same as interaction information
It is interesting to note that the mutual information (same as interaction informationInteraction information
The interaction information or co-information is one of several generalizations of the mutual information, and expresses the amount information bound up in a set of variables, beyond that which is present in any subset of those variables...
but for a change in sign) of three or more random variables can be negative as well as positive: Let X and Y be two independent fair coin flips, and let Z be their exclusive or. Then
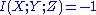 bit.
bit.Many other variations are possible for three or more random variables: for example,
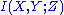 is the mutual information of the joint distribution of X and Y relative to Z, and can be interpreted as
is the mutual information of the joint distribution of X and Y relative to Z, and can be interpreted as 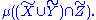 Many more complicated expressions can be built this way, and still have meaning, e.g.
Many more complicated expressions can be built this way, and still have meaning, e.g. 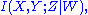 or
or