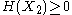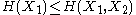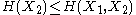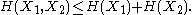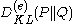Inequalities in information theory
Encyclopedia
Inequalities are very important in the study of information theory
. There are a number of different contexts in which these inequalities appear.
s on the same probability space
. For a collection of n random variables, there are 2n − 1 such non-empty subsets for which entropies can be defined. For example, when n = 2, we may consider the entropies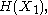
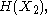and 
and 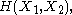express the following inequalities (which together characterize the range of the marginal and joint entropies of two random variables):
In fact, these can all be expressed as special cases of a single inequality involving the conditional mutual information
, namely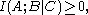
where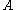
, 
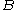, and 
each denote the joint distribution of some arbitrary (possibly empty) subset of our collection of random variables. Inequalities that can be derived from this are known as Shannon-type inequalities. More formally, (following the notation of Yeung), define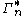 
to be the set of all constructible points in 
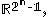where a point is said to be constructible if and only if there is a joint, discrete distribution of n random variables such that each coordinate of that point, indexed by a non-empty subset of {1, 2, ..., n}, is equal to the joint entropy of the corresponding subset of the n random variables. The closure
of
is denoted 
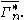
The cone
in
characterized by all Shannon-type inequalities among n random variables is denoted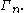 
Software has been developed to automate the task of proving such inequalities. Given an inequality, such software is able to determine whether the given inequality contains the cone 
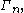in which case the inequality can be verified, since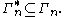 
It was shown that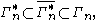
where the inclusions are proper for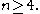
All three of these sets are, in fact, convex cone
s.
. Even the Shannon-type inequalities can be considered part of this category, since the bivariate mutual information
can be expressed as the Kullback–Leibler divergence of the joint distribution with respect to the product of the marginals, and thus these inequalities can be seen as a special case of Gibbs' inequality
.
On the other hand, it seems to be much more difficult to derive useful upper bounds for the Kullback–Leibler divergence. This is because the Kullback–Leibler divergence DKL(P||Q) depends very sensitively on events that are very rare in the reference distribution Q. DKL(P||Q) increases without bound as an event of finite non-zero probability in the distribution P becomes exceedingly rare in the reference distribution Q, and in fact DKL(P||Q) is not even defined if an event of non-zero probability in P has zero probability in Q. (Hence the requirement that P be absolutely continuous with respect to Q.)
is non-negative.
s on the real line with P absolutely continuous
with respect to Q, and whose first moments exist, then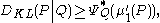
where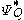
is the large deviations
rate function
, i.e. the convex conjugate
of the cumulant
-generating function, of Q, and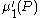
is the first moment
of P.
The Cramér–Rao bound is a corollary of this result.
s, then
where
is the Kullback–Leibler divergence in nats
and
is the total variation distance.
such that 
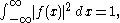and its Fourier transform
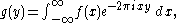the sum of the differential entropies
of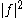
and 
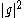is non-negative, i.e.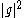
Hirschman conjectured, and it was later proved, that a sharper bound of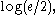
which is attained in the case of a Gaussian distribution, could replace the right-hand side of this inequality. This is especially significant since it implies, and is stronger than, Weyl's formulation of Heisenberg's uncertainty principle
.
, 
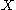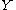, and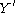 
, such that 
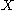takes values only in the interval [−1, 1] and 
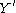is determined by 
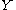(so that 
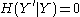), we have
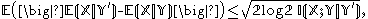
relating the conditional expectation to the conditional mutual information
. This is a simple consequence of Pinsker's inequality
. (Note: the correction factor log 2 inside the radical arises because we are measuring the conditional mutual information in bit
s rather than nats
.)
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. There are a number of different contexts in which these inequalities appear.
Shannon-type inequalities
Consider a finite collection of finitely (or at most countably) supported random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s on the same probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
. For a collection of n random variables, there are 2n − 1 such non-empty subsets for which entropies can be defined. For example, when n = 2, we may consider the entropies
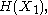
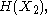and 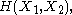and express the following inequalities (which together characterize the range of the marginal and joint entropies of two random variables):
In fact, these can all be expressed as special cases of a single inequality involving the conditional mutual information
Conditional mutual information
In probability theory, and in particular, information theory, the conditional mutual information is, in its most basic form, the expected value of the mutual information of two random variables given the value of a third.-Definition:...
, namely
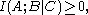
where
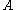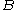, , and each denote the joint distribution of some arbitrary (possibly empty) subset of our collection of random variables. Inequalities that can be derived from this are known as Shannon-type inequalities. More formally, (following the notation of Yeung), define 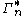to be the set of all constructible points in 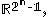where a point is said to be constructible if and only if there is a joint, discrete distribution of n random variables such that each coordinate of that point, indexed by a non-empty subset of {1, 2, ..., n}, is equal to the joint entropy of the corresponding subset of the n random variables. The closureClosure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of
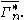
is denoted The cone
Cone (linear algebra)
In linear algebra, a cone is a subset of a vector space that is closed under multiplication by positive scalars. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V .A cone is said...
in
characterized by all Shannon-type inequalities among n random variables is denoted 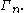Software has been developed to automate the task of proving such inequalities. Given an inequality, such software is able to determine whether the given inequality contains the cone 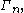in which case the inequality can be verified, since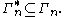 Non-Shannon-type inequalities
Other, less trivial inequalities have been discovered among the entropies and joint entropies of four or more random variables, which cannot be derived from Shannon's basic inequalities. These are known as non-Shannon-type inequalities.It was shown that
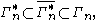
where the inclusions are proper for
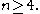All three of these sets are, in fact, convex coneConvex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
s.
Lower bounds for the Kullback–Leibler divergence
A great many important inequalities in information theory are actually lower bounds for the Kullback–Leibler divergenceKullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
. Even the Shannon-type inequalities can be considered part of this category, since the bivariate mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
can be expressed as the Kullback–Leibler divergence of the joint distribution with respect to the product of the marginals, and thus these inequalities can be seen as a special case of Gibbs' inequality
Gibbs' inequality
In information theory, Gibbs' inequality is a statement about the mathematical entropy of a discrete probability distribution. Several other bounds on the entropy of probability distributions are derived from Gibbs' inequality, including Fano's inequality....
.
On the other hand, it seems to be much more difficult to derive useful upper bounds for the Kullback–Leibler divergence. This is because the Kullback–Leibler divergence DKL(P||Q) depends very sensitively on events that are very rare in the reference distribution Q. DKL(P||Q) increases without bound as an event of finite non-zero probability in the distribution P becomes exceedingly rare in the reference distribution Q, and in fact DKL(P||Q) is not even defined if an event of non-zero probability in P has zero probability in Q. (Hence the requirement that P be absolutely continuous with respect to Q.)
Gibbs' inequality
This fundamental inequality states that the Kullback–Leibler divergenceKullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
is non-negative.
Kullback's inequality
Another inequality concerning the Kullback–Leibler divergence is known as Kullback's inequality. If P and Q are probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s on the real line with P absolutely continuous
Absolute continuity
In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
with respect to Q, and whose first moments exist, then
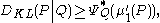
where
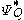is the large deviationsLarge deviations theory
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
rate function
Rate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
, i.e. the convex conjugate
Convex conjugate
In mathematics, convex conjugation is a generalization of the Legendre transformation. It is also known as Legendre–Fenchel transformation or Fenchel transformation .- Definition :...
of the cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
-generating function, of Q, and
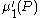is the first momentMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of P.
The Cramér–Rao bound is a corollary of this result.
Pinsker's inequality
Pinsker's inequality relates Kullback–Leibler divergence and total variation distance. It states that if P, Q are two probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s, then
where
is the Kullback–Leibler divergence in nats
Nat (information)
A nat is a logarithmic unit of information or entropy, based on natural logarithms and powers of e, rather than the powers of 2 and base 2 logarithms which define the bit. The nat is the natural unit for information entropy...
and
is the total variation distance.
Hirschman uncertainty
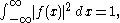In 1957, Hirschman showed that for a (reasonably well-behaved) function such that and its Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
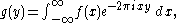the sum of the differential entropiesDifferential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
of
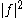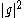and is non-negative, i.e.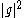Hirschman conjectured, and it was later proved, that a sharper bound of
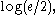which is attained in the case of a Gaussian distribution, could replace the right-hand side of this inequality. This is especially significant since it implies, and is stronger than, Weyl's formulation of Heisenberg's uncertainty principleUncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
.
Tao's inequality
Given discrete random variables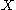, , 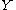and 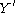, such that 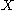takes values only in the interval [−1, 1] and 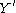is determined by 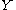(so that 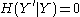), we have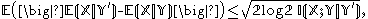relating the conditional expectation to the conditional mutual information
Conditional mutual information
In probability theory, and in particular, information theory, the conditional mutual information is, in its most basic form, the expected value of the mutual information of two random variables given the value of a third.-Definition:...
. This is a simple consequence of Pinsker's inequality
Pinsker's inequality
In information theory, Pinsker's inequality, named after its inventor Mark Semenovich Pinsker, is an inequality that relates Kullback-Leibler divergence and the total variation distance...
. (Note: the correction factor log 2 inside the radical arises because we are measuring the conditional mutual information in bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s rather than nats
Nat (information)
A nat is a logarithmic unit of information or entropy, based on natural logarithms and powers of e, rather than the powers of 2 and base 2 logarithms which define the bit. The nat is the natural unit for information entropy...
.)
See also
- Cramér–Rao bound
- Entropy power inequalityEntropy power inequalityIn mathematics, the entropy power inequality is a result in probability theory that relates to so-called "entropy power" of random variables. It shows that the entropy power of suitably well-behaved random variables is a superadditive function. The entropy power inequality was proved in 1948 by...
- Fano's inequalityFano's inequalityIn information theory, Fano's inequality relates the average information lost in a noisy channel to the probability of the categorization error. It was derived by Robert Fano in the early 1950s while teaching a Ph.D...
- Jensen's inequalityJensen's inequalityIn mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
- Kraft inequality
- Pinsker's inequalityPinsker's inequalityIn information theory, Pinsker's inequality, named after its inventor Mark Semenovich Pinsker, is an inequality that relates Kullback-Leibler divergence and the total variation distance...
- Multivariate mutual informationMultivariate mutual informationIn information theory there have been various attempts over the years to extend the definition of mutual information to more than two random variables...
External links
- Thomas M. Cover, Joy A. Thomas. Elements of Information Theory, Chapter 16, "Inequalities in Information Theory" John Wiley & Sons, Inc. 1991 Print ISBN 0471062596 Online ISBN 0471200611 pdf
- Amir Dembo, Thomas M. Cover, Joy A. Thomas. Information Theoretic Inequalities. IEEE Transactions on Information Theory, Vol. 37, No. 6, November 1991. pdf