
Conjugate points
Encyclopedia
In differential geometry, conjugate points are, roughly, points that can almost be joined by a 1-parameter family of geodesic
s. For example, on a sphere
, the north-pole and south-pole are connected by any meridian
.
, and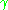 is a geodesic
is a geodesic
that connects p and q. Then p and q are conjugate points along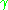 if there exists a non-zero Jacobi field
if there exists a non-zero Jacobi field
along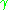 that vanishes at p and q.
that vanishes at p and q.
Recall that any Jacobi field can be written as the derivative of a geodesic variation (see the article on Jacobi field
s). Therefore, if p and q are conjugate along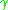 , one can construct a family of geodesics which start at p and almost end at q. In particular,
, one can construct a family of geodesics which start at p and almost end at q. In particular,
if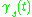 is the family of geodesics whose derivative in s at
is the family of geodesics whose derivative in s at  generates the Jacobi field J, then the end point
generates the Jacobi field J, then the end point
of the variation, namely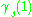 , is the point q only up to first order in s. Therefore, if two points are conjugate, it is not necessary that there exist two distinct geodesics joining them.
, is the point q only up to first order in s. Therefore, if two points are conjugate, it is not necessary that there exist two distinct geodesics joining them.
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s. For example, on a sphere
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
, the north-pole and south-pole are connected by any meridian
Meridian (geography)
A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...
.
Definition
Suppose p and q are points on a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, and
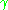 is a geodesic
is a geodesicGeodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
that connects p and q. Then p and q are conjugate points along
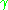 if there exists a non-zero Jacobi field
if there exists a non-zero Jacobi fieldJacobi field
In Riemannian geometry, a Jacobi field is a vector field along a geodesic \gamma in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space...
along
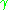 that vanishes at p and q.
that vanishes at p and q.Recall that any Jacobi field can be written as the derivative of a geodesic variation (see the article on Jacobi field
Jacobi field
In Riemannian geometry, a Jacobi field is a vector field along a geodesic \gamma in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space...
s). Therefore, if p and q are conjugate along
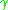 , one can construct a family of geodesics which start at p and almost end at q. In particular,
, one can construct a family of geodesics which start at p and almost end at q. In particular,if
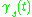 is the family of geodesics whose derivative in s at
is the family of geodesics whose derivative in s at  generates the Jacobi field J, then the end point
generates the Jacobi field J, then the end pointof the variation, namely
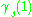 , is the point q only up to first order in s. Therefore, if two points are conjugate, it is not necessary that there exist two distinct geodesics joining them.
, is the point q only up to first order in s. Therefore, if two points are conjugate, it is not necessary that there exist two distinct geodesics joining them.Examples
- On the sphere
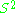 , antipodal points are conjugate.
, antipodal points are conjugate. - On
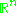 , there are no conjugate points.
, there are no conjugate points. - On Riemannian manifolds with non-positive sectional curvatureSectional curvatureIn Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
, there are no conjugate points.
See also
- cut locusCut locus (Riemannian manifold)In Riemannian geometry, the cut locus of a point p in a manifold is roughly the set of all other points for which there are multiple minimizing geodesics connecting them from p, but it may contain additional points where the minimizing geodesic is unique, under certain circumstances...
- Jacobi fieldJacobi fieldIn Riemannian geometry, a Jacobi field is a vector field along a geodesic \gamma in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space...

