
Conjunctive grammar
Encyclopedia
Conjunctive grammars are a class of formal grammars
studied in formal language
theory.
They extend the basic type of grammars,
the context-free grammars,
with a conjunction
operation.
Besides explicit conjunction,
conjunctive grammars allow implicit disjunction
represented by multiple rules for a single nonterminal symbol,
which is the only logical connective expressible in context-free grammars.
Conjunction can be used, in particular,
to specify intersection of languages.
A further extension of conjunctive grammars
known as Boolean grammar
s
additionally allows explicit negation
.
The rules of a conjunctive grammar are of the form
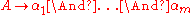
where is a nonterminal and
is a nonterminal and
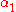 , ...,
, ..., 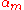
are strings formed of symbols in and
and  (finite sets of terminal and nonterminal symbols respectively).
(finite sets of terminal and nonterminal symbols respectively).
Informally, such a rule asserts that
every string over
over 
that satisfies each of the syntactical conditions represented
by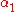 , ...,
, ..., 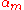
therefore satisfies the condition defined by .
.
Two equivalent formal definitions
of the language specified by a conjunctive grammar exist.
One definition is based upon representing the grammar
as a system of language equation
s with union, intersection and concatenation
and considering its least solution.
The other definition generalizes
Chomsky's generative definition of the context-free grammars
using rewriting of terms over conjunction and concatenation.
Though the expressive means of conjunctive grammars
are greater than those of context-free grammars,
conjunctive grammars retain some practically useful properties of the latter.
Most importantly, there are generalizations of the main context-free parsing algorithms,
including the linear-time recursive descent
,
the cubic-time generalized LR
,
the cubic-time Cocke-Kasami-Younger
,
as well as Valiant's algorithm running as fast as matrix multiplication.
A number of theoretical properties of conjunctive grammars have been researched,
including the expressive power of grammars over a one-letter alphabet
and numerous undecidable decision problems
.
This work provided a basis
for the study language equation
s of a more general form.
studied in formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
theory.
They extend the basic type of grammars,
the context-free grammars,
with a conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
operation.
Besides explicit conjunction,
conjunctive grammars allow implicit disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
represented by multiple rules for a single nonterminal symbol,
which is the only logical connective expressible in context-free grammars.
Conjunction can be used, in particular,
to specify intersection of languages.
A further extension of conjunctive grammars
known as Boolean grammar
Boolean grammar
Boolean grammars are a class of formal grammars studied in formal language theory. They extend the basic type of grammars, the context-free grammars, with conjunction and negation operations...
s
additionally allows explicit negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
.
The rules of a conjunctive grammar are of the form
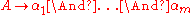
where
 is a nonterminal and
is a nonterminal and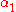 , ...,
, ..., 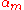
are strings formed of symbols in
 and
and  (finite sets of terminal and nonterminal symbols respectively).
(finite sets of terminal and nonterminal symbols respectively).Informally, such a rule asserts that
every string
 over
over 
that satisfies each of the syntactical conditions represented
by
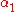 , ...,
, ..., 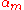
therefore satisfies the condition defined by
 .
.Two equivalent formal definitions
of the language specified by a conjunctive grammar exist.
One definition is based upon representing the grammar
as a system of language equation
Language equation
Language equations are mathematical statements that resemble numerical equations, but the variables assume values of formal languages rather than numbers. Instead of arithmetic operations in numerical equations, the variables are joined by language operations...
s with union, intersection and concatenation
and considering its least solution.
The other definition generalizes
Chomsky's generative definition of the context-free grammars
using rewriting of terms over conjunction and concatenation.
Though the expressive means of conjunctive grammars
are greater than those of context-free grammars,
conjunctive grammars retain some practically useful properties of the latter.
Most importantly, there are generalizations of the main context-free parsing algorithms,
including the linear-time recursive descent
Recursive descent parser
A recursive descent parser is a top-down parser built from a set of mutually-recursive procedures where each such procedure usually implements one of the production rules of the grammar...
,
the cubic-time generalized LR
GLR parser
A GLR parser is an extension of an LR parser algorithm to handle nondeterministic and ambiguous grammars. First described in a 1984 paper by Masaru Tomita, it has also been referred to as a "parallel parser"...
,
the cubic-time Cocke-Kasami-Younger
CYK algorithm
The Cocke–Younger–Kasami algorithm is a parsing algorithm for context-free grammars. It employs bottom-up parsing and dynamic programming....
,
as well as Valiant's algorithm running as fast as matrix multiplication.
A number of theoretical properties of conjunctive grammars have been researched,
including the expressive power of grammars over a one-letter alphabet
and numerous undecidable decision problems
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
.
This work provided a basis
for the study language equation
Language equation
Language equations are mathematical statements that resemble numerical equations, but the variables assume values of formal languages rather than numbers. Instead of arithmetic operations in numerical equations, the variables are joined by language operations...
s of a more general form.
External links
- Artur Jeż. Conjunctive grammars can generate non-regular unary languages. Slides of talk held at the International Conference on Developments in Language TheoryInternational Conference on Developments in Language TheoryDLT, the International Conference on Developments in Language Theory is an academic conference in the fieldof computer scienceheld annually under the auspices of the European Association for Theoretical Computer Science...
2007. - Alexander Okhotin's page on conjunctive grammars.
- Alexander Okhotin. Nine open problems for conjunctive and Boolean grammars.

