Constructible set (topology)
Encyclopedia
In topology
, a constructible set in a noetherian topological space
is a finite union of locally closed sets. (A set is locally closed if it is the intersection of an open set and closed set, or equivalently, if it is open in its closure.) Constructible sets form a Boolean algebra (i.e., it is closed under finite union and complementation.) In fact, the constructible sets are precisely the Boolean algebra generated by open sets and closed sets; hence, the name "constructible". The notion appears in classical algebraic geometry
.
Chevalley's theorem (EGA IV, 1.8.4.) states: Let
be a morphism of finite presentations of schemes. Then the image of any constructible set under f is constructible. In particular, the image of a variety need not be a variety, but is (under the assumptions) always a constructible set. For example, the variety 
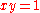(the hyperbola) has image under projecting to the x-axis of the x-axis minus the origin: this is constructible but not a variety, and neither open nor closed in the plane.
In a topological space, every constructible set contains a dense open subset of its closure.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a constructible set in a noetherian topological space
Noetherian topological space
In mathematics, a Noetherian topological space is a topological space in which closed subsets satisfy the descending chain condition. Equivalently, we could say that the open subsets satisfy the ascending chain condition, since they are the complements of the closed subsets...
is a finite union of locally closed sets. (A set is locally closed if it is the intersection of an open set and closed set, or equivalently, if it is open in its closure.) Constructible sets form a Boolean algebra (i.e., it is closed under finite union and complementation.) In fact, the constructible sets are precisely the Boolean algebra generated by open sets and closed sets; hence, the name "constructible". The notion appears in classical algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
Chevalley's theorem (EGA IV, 1.8.4.) states: Let
be a morphism of finite presentations of schemes. Then the image of any constructible set under f is constructible. In particular, the image of a variety need not be a variety, but is (under the assumptions) always a constructible set. For example, the variety 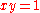(the hyperbola) has image under projecting to the x-axis of the x-axis minus the origin: this is constructible but not a variety, and neither open nor closed in the plane.In a topological space, every constructible set contains a dense open subset of its closure.