Convection–diffusion equation
Encyclopedia
The convection–diffusion equation is a parabolic partial differential equation
combining the diffusion equation and the advection
equation, which describes
physical phenomena where particles or energy (or other physical quantities) are transferred inside a physical system due to two processes: diffusion
and convection
. In its simplest form (when the diffusion coefficient and the convection velocity are constant and there are no sources or sinks) the equation takes the form:
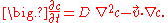
The two terms on the right hand side represent different physical processes: the first corresponds to normal diffusion
while the second describes convection
or advection
– which is why the equation is also known as the advection–diffusion equation. c is the variable of interest (species concentration for mass transfer, temperature for heat transfer), the constant D is the diffusivity for mass or heat transfer
, and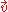
is the velocity.
Stationary convection-diffusion equation refers to this same equation with the time derivative omitted.
, which states that the rate of change for a scalar quantity in a differential control volume is given by flow and diffusion into and out of that part of the system along with any generation or consumption inside the control volume:
where
is the total flux
and s is a net volumetric source for c. This flux can be written using the phenomenological Fick's first law, which assumes that the flux of the diffusing material relative to the bulk motion in any part of the system is proportional to the local concentration gradient
. When there is convection or flow, the total flux in a stationary coordinate system is given by the sum of the diffusive flux in the material frame and what is known as the convective flux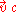
.
Combining these two terms the total flux becomes:
The substitution of this equation into the continuity equation gives the general form of the convection–diffusion equation:
In general, D,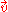
, and s may vary with space and time. In cases in which they depend on concentration as well, the equation becomes nonlinear, giving rise to many distinctive mixing phenomena such as Rayleigh–Bénard convection
when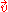
depends on temperature in the heat transfer formulation and reaction-diffusion
pattern formation when s depends on concentration in the mass transfer formulation.
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
combining the diffusion equation and the advection
Advection
Advection, in chemistry, engineering and earth sciences, is a transport mechanism of a substance, or a conserved property, by a fluid, due to the fluid's bulk motion in a particular direction. An example of advection is the transport of pollutants or silt in a river. The motion of the water carries...
equation, which describes
physical phenomena where particles or energy (or other physical quantities) are transferred inside a physical system due to two processes: diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
and convection
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
. In its simplest form (when the diffusion coefficient and the convection velocity are constant and there are no sources or sinks) the equation takes the form:
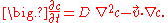
The two terms on the right hand side represent different physical processes: the first corresponds to normal diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
while the second describes convection
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
or advection
Advection
Advection, in chemistry, engineering and earth sciences, is a transport mechanism of a substance, or a conserved property, by a fluid, due to the fluid's bulk motion in a particular direction. An example of advection is the transport of pollutants or silt in a river. The motion of the water carries...
– which is why the equation is also known as the advection–diffusion equation. c is the variable of interest (species concentration for mass transfer, temperature for heat transfer), the constant D is the diffusivity for mass or heat transfer
Thermal diffusivity
In heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It has the SI unit of m²/s...
, and
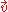is the velocity.Stationary convection-diffusion equation refers to this same equation with the time derivative omitted.
Derivation
The convection–diffusion equation can be derived in a straightforward way from the continuity equationContinuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
, which states that the rate of change for a scalar quantity in a differential control volume is given by flow and diffusion into and out of that part of the system along with any generation or consumption inside the control volume:
where
is the total fluxFlux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
and s is a net volumetric source for c. This flux can be written using the phenomenological Fick's first law, which assumes that the flux of the diffusing material relative to the bulk motion in any part of the system is proportional to the local concentration gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
. When there is convection or flow, the total flux in a stationary coordinate system is given by the sum of the diffusive flux in the material frame and what is known as the convective flux
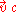.Combining these two terms the total flux becomes:
The substitution of this equation into the continuity equation gives the general form of the convection–diffusion equation:
In general, D,
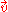, and s may vary with space and time. In cases in which they depend on concentration as well, the equation becomes nonlinear, giving rise to many distinctive mixing phenomena such as Rayleigh–Bénard convectionRayleigh–Bénard convection
Rayleigh–Bénard convection is a type of natural convection, occurring in a plane of fluid heated from below, in which the fluid develops a regular pattern of convection cells known as Bénard cells. Rayleigh–Bénard convection is one of the most commonly studied convection phenomena because of its...
when
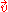depends on temperature in the heat transfer formulation and reaction-diffusionReaction–diffusion system
Reaction–diffusion systems are mathematical models which explain how the concentration of one or more substances distributed in space changes under the influence of two processes: local chemical reactions in which the substances are transformed into each other, and diffusion which causes the...
pattern formation when s depends on concentration in the mass transfer formulation.