Convexity (finance)
Encyclopedia
In mathematical finance
, convexity refers to non-linearities in a financial model. In other words, if the price of an underlying variable changes, the price of an output does not change linearly, but depends on the second derivative
(or, loosely speaking, higher-order terms) of the modeling function. Geometrically, the model is no longer flat but curved, and the degree of curvature is called the convexity.
. In practice the most significant of these is bond convexity
, the second derivative of bond price with respect to interest rates.
As the second derivative is the first non-linear term, and thus often the most significant, "convexity" is also used loosely to refer to non-linearities generally, including higher-order terms. Refining a model to account for non-linearities is called "correcting for convexity" or adding a convexity correction.
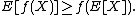
Geometrically, if the model price curves up on both sides of the present value (the payoff function is convex up, and is above a tangent line at that point), then if the price of the underlying changes, the price of the output is greater than is modeled using only the first derivative. Conversely, if the model price curves down (the convexity is negative, the payoff function is below the tangent line), the price of the output is lower than is modeled using only the first derivative.
The precise convexity adjustment depends on the model of future price movements of the underlying (the probability distribution) and on the model of the price, though it is linear in the convexity (second derivative of the price function).
In Black–Scholes pricing of options, omitting interest rates and the first derivative, the Black–Scholes equation reduces to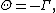
"(infinitesimally) the time value is the convexity". That is, the value of a option is due to the convexity of the ultimate payout: one has the option to buy an asset or not (in a call; for a put it is an option to sell), and the ultimate payout function (a hockey stick
shape) is convex – "optionality" corresponds to convexity in the payout. Thus, if one purchases a call option, the expected value of the option is higher than simply taking the expected future value of the underlying and inputting it into the option payout function: the expected value of a convex function is higher than the function of the expected value (Jensen inequality). The price of the option – the value of the optionality – thus reflects the convexity of the payoff function.
This value is isolated via a straddle
– purchasing an at-the-money straddle (whose value increases if the price of the underlying increases or decreases) has (initially) no delta: one is simply purchasing convexity (optionality), without taking a position on the underlying asset – one benefits from the degree of movement, not the direction.
From the point of view of risk management, being long convexity (having positive Gamma and hence (ignoring interest rates and Delta) negative Theta) means that one benefits from volatility (positive Gamma), but loses money over time (negative Theta) – one net profits if prices move more than expected, and net lose if prices move less than expected.
s, such as constant maturity swap
(CMSs), among others.
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
, convexity refers to non-linearities in a financial model. In other words, if the price of an underlying variable changes, the price of an output does not change linearly, but depends on the second derivative
Second derivative
In calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
(or, loosely speaking, higher-order terms) of the modeling function. Geometrically, the model is no longer flat but curved, and the degree of curvature is called the convexity.
Terminology
Strictly speaking, convexity refers to the second derivative of output price with respect to an input price. In derivative pricing, this is referred to as Gamma (Γ), one of the GreeksGreeks (finance)
In mathematical finance, the Greeks are the quantities representing the sensitivities of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of...
. In practice the most significant of these is bond convexity
Bond convexity
In finance, convexity is a measure of the sensitivity of the duration of a bond to changes in interest rates, the second derivative of the price of the bond with respect to interest rates . In general, the higher the convexity, the more sensitive the bond price is to decreasing interest rates and...
, the second derivative of bond price with respect to interest rates.
As the second derivative is the first non-linear term, and thus often the most significant, "convexity" is also used loosely to refer to non-linearities generally, including higher-order terms. Refining a model to account for non-linearities is called "correcting for convexity" or adding a convexity correction.
Mathematics
Formally, the convexity adjustment arises from the Jensen inequality in probability theory: the expected value of a convex function is greater than or equal to the function of the expected value: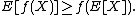Geometrically, if the model price curves up on both sides of the present value (the payoff function is convex up, and is above a tangent line at that point), then if the price of the underlying changes, the price of the output is greater than is modeled using only the first derivative. Conversely, if the model price curves down (the convexity is negative, the payoff function is below the tangent line), the price of the output is lower than is modeled using only the first derivative.
The precise convexity adjustment depends on the model of future price movements of the underlying (the probability distribution) and on the model of the price, though it is linear in the convexity (second derivative of the price function).
Interpretation
The convexity can be used to interpret derivative pricing: mathematically, convexity is optionality – the price of an option (the value of optionality) corresponds to the convexity of the underlying payout.In Black–Scholes pricing of options, omitting interest rates and the first derivative, the Black–Scholes equation reduces to
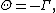"(infinitesimally) the time value is the convexity". That is, the value of a option is due to the convexity of the ultimate payout: one has the option to buy an asset or not (in a call; for a put it is an option to sell), and the ultimate payout function (a hockey stickHockey stick
A hockey stick is a piece of equipment used in field hockey, ice hockey or roller hockey to move the ball or puck.- Field hockey :Field hockey sticks have an end which varies in shape, often depending on the players position...
shape) is convex – "optionality" corresponds to convexity in the payout. Thus, if one purchases a call option, the expected value of the option is higher than simply taking the expected future value of the underlying and inputting it into the option payout function: the expected value of a convex function is higher than the function of the expected value (Jensen inequality). The price of the option – the value of the optionality – thus reflects the convexity of the payoff function.
This value is isolated via a straddle
Straddle
In finance, a straddle is an investment strategy involving the purchase or sale of particular option derivatives that allows the holder to profit based on how much the price of the underlying security moves, regardless of the direction of price movement...
– purchasing an at-the-money straddle (whose value increases if the price of the underlying increases or decreases) has (initially) no delta: one is simply purchasing convexity (optionality), without taking a position on the underlying asset – one benefits from the degree of movement, not the direction.
From the point of view of risk management, being long convexity (having positive Gamma and hence (ignoring interest rates and Delta) negative Theta) means that one benefits from volatility (positive Gamma), but loses money over time (negative Theta) – one net profits if prices move more than expected, and net lose if prices move less than expected.
Application
Convexity is used ubiquitously in modeling of bonds and derivatives. Beyond bond convexity and the Gamma of options, it is particularly relevant to interest rate derivativeInterest rate derivative
An interest rate derivative is a derivative where the underlying asset is the right to pay or receive a notional amount of money at a given interest rate...
s, such as constant maturity swap
Constant maturity swap
A constant maturity swap, also known as a CMS, is a swap that allows the purchaser to fix the duration of received flows on a swap.The floating leg of an interest rate swap typically resets against a published index...
(CMSs), among others.