
Greeks (finance)
Encyclopedia
In mathematical finance
, the Greeks are the quantities representing the sensitivities of the price of derivatives
such as options
to a change in underlying parameter
s on which the value of an instrument or portfolio
of financial instruments is dependent. The name is used because the most common of these sensitivities are often denoted by Greek letters
. Collectively these have also been called the risk sensitivities, risk measures or hedge parameters.
The Greeks are vital tools in risk management
. Each Greek measures the sensitivity
of the value of a portfolio to a small change in a given underlying parameter, so that component risks may be treated in isolation, and the portfolio rebalanced accordingly to achieve a desired exposure; see for example delta hedging.
The Greeks in the Black–Scholes model are relatively easy to calculate, a desirable property of financial
models
, and are very useful for derivatives traders, especially those who seek to hedge their portfolios from adverse changes in market conditions. For this reason, those Greeks which are particularly useful for hedging delta, theta, and vega are well-defined for measuring changes in Price, Time and Volatility. Although rho is a primary input into the Black–Scholes model, the overall impact on the value of an option corresponding to changes in the risk-free interest rate
is generally insignificant and therefore higher-order derivatives involving the risk-free interest rate are not common.
The most common of the Greeks are the first order derivatives: Delta, Vega, Theta and Rho as well as Gamma, a second-order derivative of the value function. The remaining sensitivities in this list are common enough that they have common names, but this list is by no means exhaustive.
Delta
Delta
, , measures the rate of change of option value with respect to changes in the underlying asset's price. Delta is the first derivative
, measures the rate of change of option value with respect to changes in the underlying asset's price. Delta is the first derivative
of the value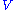 of the option with respect to the underlying instrument's price
of the option with respect to the underlying instrument's price 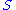 .
.
and 0.0 and −1.0 for a long put (and/or short call)
– depending on price, a call option behaves as if one owns 1 share of the underlying stock (if deep in the money), or owns nothing (if far out of the money), or something in between, and conversely for a put option.
These numbers are commonly presented as a percentage of the total number of shares represented by the option contract(s). This is convenient because the option will (instantaneously) behave like the number of shares indicated by the delta. For example, if a portfolio of 100 American call options on XYZ each have a delta of 0.25 (=25%), it will gain or lose value just like 25 shares of XYZ as the price changes for small price movements.
Delta is always positive for long calls and negative for long puts (unless they are zero). The total delta of a complex portfolio of positions on the same underlying asset can be calculated by simply taking the sum of the deltas for each individual position – delta of a portfolio is linear in the constituents. Since the delta of underlying asset is always 1.0, the trader could delta-hedge
his entire position in the underlying by buying or shorting the number of shares indicated by the total delta. For example, if a portfolio of options in XYZ (expressed as shares of the underlying) is +2.75, the trader would be able to delta-hedge the portfolio by selling short 2.75 shares of the underlying. This portfolio will then retain its total value regardless of which direction the price of XYZ moves. (Albeit for only small movements of the underlying, a short amount of time and not-withstanding changes in other market conditions such as volatility and the rate of return for a risk-free investment).
). For example, if an out-of-the-money call option has a delta of 0.15, the trader might estimate that the option has appropriately a 15% chance of expiring in-the-money. Similarly, if a put contract has a delta of −0.25, the trader might expect the option to have a 25% probability of expiring in-the-money. At-the-money puts and calls have a delta of approximately 0.5 and −0.5 respectively (however, this approximation rapidly goes out the window when looking at a term of just a few years, with the ATM call commonly having a delta over 0.60 or 0.70), or each will have a 50% chance of expiring in-the-money. The correct, exact calculation for the probability of an option finishing in the money is its Dual Delta, which is the first derivative of option price with respect to strike.
: a long call plus a short put (a call minus a put) replicates a forward, which has delta equal to 1.
If the value of delta for an option is known, one can compute the value of the option of the same strike price, underlying and maturity but opposite right by subtracting 1 from the known value. For example, if the delta of a call is 0.42 then one can compute the delta of the corresponding put at the same strike price by 0.42 − 1 = −0.58. While in deriving delta of a call from put will not follow this approach e.g. – delta of a put is −0.58 and if we follow the same approach then delta of a call with same strike should be −1.58. so delta should be = opposite sign ( abs(delta) − 1).
Vega
Vega measures sensitivity to volatility
. Vega is the derivative of the option value with respect to the volatility
of the underlying asset.
Vega is not the name of any Greek letter. However, the glyph used is the Greek letter nu. Presumably the name vega was adopted because the Greek letter nu looked like a Latin vee, and vega was derived from vee by analogy with how beta, eta, and theta are pronounced in English.
The symbol kappa
, , is sometimes used (by academics) instead of vega (as is tau (
, is sometimes used (by academics) instead of vega (as is tau ( ), though this is rare).
), though this is rare).
Vega can be an important Greek to monitor for an option trader, especially in volatile markets, since the value of some option strategies can be particularly sensitive to changes in volatility. The value of an option straddle
, for example, is extremely dependent on changes to volatility.
Theta
Theta, , measures the sensitivity of the value of the derivative to the passage of time (see Option time value
, measures the sensitivity of the value of the derivative to the passage of time (see Option time value
): the "time decay."
The value of an option can be analysed into two parts: the intrinsic value
and the time value. The intrinsic value is the amount of money you would gain if you exercised the option immediately, so a call with strike $50 on a stock with price $60 would have intrinsic value of $10, whereas the corresponding put would have zero intrinsic value. The time value is the value of having the option of waiting longer before deciding to exercise. Even a deeply out of the money put will be worth something, as there is some chance the stock price will fall below the strike before the expiry date. However, as time approaches maturity, there is less chance of this happening, so the time value of an option is decreasing with time. Thus if you are long an option you are short theta: your portfolio will lose value with the passage of time (all other factors held constant).
Rho
Rho
,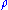 , measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk free interest rate (for the relevant outstanding term). Except under extreme circumstances, the value of an option is less sensitive to changes in the risk free interest rate than to changes in other parameters. For this reason, rho is the least used of the first-order Greeks.
, measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk free interest rate (for the relevant outstanding term). Except under extreme circumstances, the value of an option is less sensitive to changes in the risk free interest rate than to changes in other parameters. For this reason, rho is the least used of the first-order Greeks.
Charm or delta decay, measures the instantaneous rate of change of delta over the passage of time. Charm has also been called DdeltaDtime. Charm can be an important Greek to measure/monitor when delta-hedging a position over a weekend. Charm is a second-order derivative of the option value, once to price and once to the passage of time. It is also then the derivative of theta with respect to the underlying's price.
Color, gamma decay or DgammaDtime measures the rate of change of gamma over the passage of time. Color is a third-order derivative of the option value, twice to underlying asset price and once to time. Color can be an important sensitivity to monitor when maintaining a gamma-hedged portfolio as it can help the trader to anticipate the effectiveness of the hedge as time passes.
DvegaDtime, measures the rate of change in the vega with respect to the passage of time. DvegaDtime is the second derivative of the value function; once to volatility and once to time.
Gamma
Gamma, , measures the rate of change in the delta with respect to changes in the underlying price. Gamma is the second derivative
, measures the rate of change in the delta with respect to changes in the underlying price. Gamma is the second derivative
of the value function with respect to the underlying price. All long options have positive gamma and all short options have negative gamma. Gamma is greatest approximately at-the-money (ATM) and diminishes the further out you go either in-the-money (ITM) or out-of-the-money (OTM). Gamma is important because it corrects for the convexity
of value.
When a trader seeks to establish an effective delta-hedge for a portfolio, the trader may also seek to neutralize the portfolio's gamma, as this will ensure that the hedge will be effective over a wider range of underlying price movements. However, in neutralizing the gamma of a portfolio, alpha (the return in excess of the risk-free rate) is reduced.
Lambda
, , omega
, omega
, , or elasticity is the percentage
, or elasticity is the percentage
change in option value per percentage
change in the underlying price, a measure of leverage
, sometimes called gearing.
Speed measures the rate of change in Gamma with respect to changes in the underlying price. This is also sometimes referred to as the gamma of the gamma or DgammaDspot. Speed is the third derivative of the value function with respect to the underlying spot price. Speed can be important to monitor when delta-hedging or gamma-hedging a portfolio.
Ultima measures the sensitivity of the option vomma with respect to change in volatility. Ultima has also been referred to as DvommaDvol. Ultima is a third-order derivative of the option value to volatility.
\frac{\partial^2 V}{\partial S \partial \sigma}
|}
Vanna, also referred to as DvegaDspot and DdeltaDvol, is a second order derivative of the option value, once to the underlying spot price and once to volatility. It is mathematically equivalent to DdeltaDvol, the sensitivity of the option delta with respect to change in volatility; or alternatively, the partial of vega with respect to the underlying instrument's price. Vanna can be a useful sensitivity to monitor when maintaining a delta- or vega-hedged portfolio as vanna will help the trader to anticipate changes to the effectiveness of a delta-hedge as volatility changes or the effectiveness of a vega-hedge against change in the underlying spot price.
Vomma, Volga, Vega Convexity, Vega gamma or dTau/dVol measures second order sensitivity to volatility
. Vomma is the second derivative of the option value with respect to the volatility, or, stated another way, vomma measures the rate of change to vega as volatility changes. With positive vomma, a position will become long vega as implied volatility increases and short vega as it decreases, which can be scalped in a way analogous to long gamma. And an initially vega-neutral, long-vomma position can be constructed from ratios of options at different strikes. Vomma is positive for options away from the money, and initially increases with distance from the money (but drops off as vega drops off). (Specifically, vomma is positive where the usual d1 and d2 terms are of the same sign, which is true when d2 < 0 or d1 > 0.)
Zomma measures the rate of change of gamma with respect to changes in volatility. Zomma has also been referred to as DgammaDvol. Zomma is the third derivative of the option value, twice to underlying asset price and once to volatility. Zomma can be a useful sensitivity to monitor when maintaining a gamma-hedged portfolio as zomma will help the trader to anticipate changes to the effectiveness of the hedge as volatility changes.
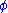 (phi) is the standard normal probability density function
(phi) is the standard normal probability density function
and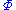 is the standard normal cumulative distribution function
is the standard normal cumulative distribution function
. Note that the gamma and vega formulas are the same for calls
and puts
.
For a given:
Stock Price ,
,
Strike Price ,
,
Risk-Free Rate ,
,
Annual Dividend Yield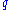 ,
,
Time to Maturity,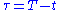 , and
, and
Volatility ...
...
where
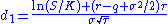

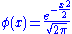

are used analogously to the delta of an option. The closest analogue to the delta is DV01, which is the reduction in price (in currency units) for an increase of one basis point
(i.e. 0.01% per annum) in the yield (the yield is the underlying variable).
Analogous to the lambda is the modified duration, which is the percentage change in the market price of the bond(s) for a unit change in the yield (i.e. it is equivalent to DV01 divided by the market price). Unlike the lambda, which is an elasticity
(a percentage change in output for a percentage change in input), the modified duration is instead a semi-elasticity—a percentage change in output for a unit change in input.
is the optimal date to exercise an American or Bermudan option. It is useful to compute it for hedging purposes—for example, one can represent flows of an American swaption like the flows of a swap starting at the fugit multiplied by delta, then use these to compute sensitivities.
Theory
Online tools
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
, the Greeks are the quantities representing the sensitivities of the price of derivatives
Derivative (finance)
A derivative instrument is a contract between two parties that specifies conditions—in particular, dates and the resulting values of the underlying variables—under which payments, or payoffs, are to be made between the parties.Under U.S...
such as options
Option (finance)
In finance, an option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the...
to a change in underlying parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s on which the value of an instrument or portfolio
Portfolio (finance)
Portfolio is a financial term denoting a collection of investments held by an investment company, hedge fund, financial institution or individual.-Definition:The term portfolio refers to any collection of financial assets such as stocks, bonds and cash...
of financial instruments is dependent. The name is used because the most common of these sensitivities are often denoted by Greek letters
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
. Collectively these have also been called the risk sensitivities, risk measures or hedge parameters.
Use of the Greeks
EWLINE
|
||||
|
The Greeks are vital tools in risk management
Financial risk management
Financial risk management is the practice of creating economic value in a firm by using financial instruments to manage exposure to risk, particularly credit risk and market risk. Other types include Foreign exchange, Shape, Volatility, Sector, Liquidity, Inflation risks, etc...
. Each Greek measures the sensitivity
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
of the value of a portfolio to a small change in a given underlying parameter, so that component risks may be treated in isolation, and the portfolio rebalanced accordingly to achieve a desired exposure; see for example delta hedging.
The Greeks in the Black–Scholes model are relatively easy to calculate, a desirable property of financial
Financial market
In economics, a financial market is a mechanism that allows people and entities to buy and sell financial securities , commodities , and other fungible items of value at low transaction costs and at prices that reflect supply and demand.Both general markets and...
models
Model (economics)
In economics, a model is a theoretical construct that represents economic processes by a set of variables and a set of logical and/or quantitative relationships between them. The economic model is a simplified framework designed to illustrate complex processes, often but not always using...
, and are very useful for derivatives traders, especially those who seek to hedge their portfolios from adverse changes in market conditions. For this reason, those Greeks which are particularly useful for hedging delta, theta, and vega are well-defined for measuring changes in Price, Time and Volatility. Although rho is a primary input into the Black–Scholes model, the overall impact on the value of an option corresponding to changes in the risk-free interest rate
Risk-free interest rate
Risk-free interest rate is the theoretical rate of return of an investment with no risk of financial loss. The risk-free rate represents the interest that an investor would expect from an absolutely risk-free investment over a given period of time....
is generally insignificant and therefore higher-order derivatives involving the risk-free interest rate are not common.
The most common of the Greeks are the first order derivatives: Delta, Vega, Theta and Rho as well as Gamma, a second-order derivative of the value function. The remaining sensitivities in this list are common enough that they have common names, but this list is by no means exhaustive.
Delta 
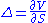 |
Delta
Delta (letter)
Delta is the fourth letter of the Greek alphabet. In the system of Greek numerals it has a value of 4. It was derived from the Phoenician letter Dalet...
,
 , measures the rate of change of option value with respect to changes in the underlying asset's price. Delta is the first derivative
, measures the rate of change of option value with respect to changes in the underlying asset's price. Delta is the first derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
of the value
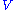 of the option with respect to the underlying instrument's price
of the option with respect to the underlying instrument's price 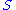 .
.Practical use
For a vanilla option, delta will be a number between 0.0 and 1.0 for a long call (and/or short put)Call option
A call option, often simply labeled a "call", is a financial contract between two parties, the buyer and the seller of this type of option. The buyer of the call option has the right, but not the obligation to buy an agreed quantity of a particular commodity or financial instrument from the seller...
and 0.0 and −1.0 for a long put (and/or short call)
Put option
A put or put option is a contract between two parties to exchange an asset, the underlying, at a specified price, the strike, by a predetermined date, the expiry or maturity...
– depending on price, a call option behaves as if one owns 1 share of the underlying stock (if deep in the money), or owns nothing (if far out of the money), or something in between, and conversely for a put option.
These numbers are commonly presented as a percentage of the total number of shares represented by the option contract(s). This is convenient because the option will (instantaneously) behave like the number of shares indicated by the delta. For example, if a portfolio of 100 American call options on XYZ each have a delta of 0.25 (=25%), it will gain or lose value just like 25 shares of XYZ as the price changes for small price movements.
Delta is always positive for long calls and negative for long puts (unless they are zero). The total delta of a complex portfolio of positions on the same underlying asset can be calculated by simply taking the sum of the deltas for each individual position – delta of a portfolio is linear in the constituents. Since the delta of underlying asset is always 1.0, the trader could delta-hedge
Delta neutral
In finance, delta neutral describes a portfolio of related financial securities, in which the portfolio value remains unchanged due to small changes in the value of the underlying security...
his entire position in the underlying by buying or shorting the number of shares indicated by the total delta. For example, if a portfolio of options in XYZ (expressed as shares of the underlying) is +2.75, the trader would be able to delta-hedge the portfolio by selling short 2.75 shares of the underlying. This portfolio will then retain its total value regardless of which direction the price of XYZ moves. (Albeit for only small movements of the underlying, a short amount of time and not-withstanding changes in other market conditions such as volatility and the rate of return for a risk-free investment).
As a proxy for probability
Some option traders also use the absolute value of delta as the probability that the option will expire in-the-money (if the market moves under Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
). For example, if an out-of-the-money call option has a delta of 0.15, the trader might estimate that the option has appropriately a 15% chance of expiring in-the-money. Similarly, if a put contract has a delta of −0.25, the trader might expect the option to have a 25% probability of expiring in-the-money. At-the-money puts and calls have a delta of approximately 0.5 and −0.5 respectively (however, this approximation rapidly goes out the window when looking at a term of just a few years, with the ATM call commonly having a delta over 0.60 or 0.70), or each will have a 50% chance of expiring in-the-money. The correct, exact calculation for the probability of an option finishing in the money is its Dual Delta, which is the first derivative of option price with respect to strike.
Relationship between call and put delta
Given a European call and put option for the same underlying, strike price and time to maturity, and with no dividend yield, the sum of the absolute values of the delta of each option will be 1.00 – more precisely, the delta of the call (positive) minus the delta of the put (negative) equals 1. This is due to put–call parityPut–call parity
In financial mathematics, put–call parity defines a relationship between the price of a European call option and European put option in a frictionless market —both with the identical strike price and expiry, and the underlying being a liquid asset. In the absence of liquidity, the existence of a...
: a long call plus a short put (a call minus a put) replicates a forward, which has delta equal to 1.
If the value of delta for an option is known, one can compute the value of the option of the same strike price, underlying and maturity but opposite right by subtracting 1 from the known value. For example, if the delta of a call is 0.42 then one can compute the delta of the corresponding put at the same strike price by 0.42 − 1 = −0.58. While in deriving delta of a call from put will not follow this approach e.g. – delta of a put is −0.58 and if we follow the same approach then delta of a call with same strike should be −1.58. so delta should be = opposite sign ( abs(delta) − 1).
Vega 
 |
Vega measures sensitivity to volatility
Volatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
. Vega is the derivative of the option value with respect to the volatility
Volatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
of the underlying asset.
Vega is not the name of any Greek letter. However, the glyph used is the Greek letter nu. Presumably the name vega was adopted because the Greek letter nu looked like a Latin vee, and vega was derived from vee by analogy with how beta, eta, and theta are pronounced in English.
The symbol kappa
Kappa
Kappa is the 10th letter of the Greek alphabet, used to represent the voiceless velar stop, or "k", sound in Ancient and Modern Greek. In the system of Greek numerals it has a value of 20. It was derived from the Phoenician letter Kaph...
,
 , is sometimes used (by academics) instead of vega (as is tau (
, is sometimes used (by academics) instead of vega (as is tau ( ), though this is rare).
), though this is rare).Practical use
Vega is typically expressed as the amount of money per underlying share that the option's value will gain or lose as volatility rises or falls by 1%.Vega can be an important Greek to monitor for an option trader, especially in volatile markets, since the value of some option strategies can be particularly sensitive to changes in volatility. The value of an option straddle
Straddle
In finance, a straddle is an investment strategy involving the purchase or sale of particular option derivatives that allows the holder to profit based on how much the price of the underlying security moves, regardless of the direction of price movement...
, for example, is extremely dependent on changes to volatility.
Theta 
 |
Theta,
 , measures the sensitivity of the value of the derivative to the passage of time (see Option time value
, measures the sensitivity of the value of the derivative to the passage of time (see Option time valueOption time value
In finance, the time value of an option is the premium a rational investor would pay over its current exercise value , based on its potential to increase in value before expiring. This probability is always greater than zero, thus an option is always worth more than its current exercise value...
): the "time decay."
Practical use
The mathematical result of the formula for theta (see below) is expressed in value per year. By convention, it is usual to divide the result by the number of days in a year, to arrive at the amount of money per share of the underlying that the option loses in one day. Theta is almost always negative for long calls and puts and positive for short (or written) calls and puts. An exception is a deep in-the-money European put. The total theta for a portfolio of options can be determined by summing the thetas for each individual position.The value of an option can be analysed into two parts: the intrinsic value
Intrinsic value (finance)
In finance, intrinsic value refers to the value of a security which is intrinsic to or contained in the security itself. It is also frequently called fundamental value. It is ordinarily calculated by summing the future income generated by the asset, and discounting it to the present value...
and the time value. The intrinsic value is the amount of money you would gain if you exercised the option immediately, so a call with strike $50 on a stock with price $60 would have intrinsic value of $10, whereas the corresponding put would have zero intrinsic value. The time value is the value of having the option of waiting longer before deciding to exercise. Even a deeply out of the money put will be worth something, as there is some chance the stock price will fall below the strike before the expiry date. However, as time approaches maturity, there is less chance of this happening, so the time value of an option is decreasing with time. Thus if you are long an option you are short theta: your portfolio will lose value with the passage of time (all other factors held constant).
Rho 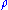
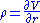 |
Rho
Rho (letter)
Rho is the 17th letter of the Greek alphabet. In the system of Greek numerals, it has a value of 100. It is derived from Semitic resh "head"...
,
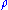 , measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk free interest rate (for the relevant outstanding term). Except under extreme circumstances, the value of an option is less sensitive to changes in the risk free interest rate than to changes in other parameters. For this reason, rho is the least used of the first-order Greeks.
, measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk free interest rate (for the relevant outstanding term). Except under extreme circumstances, the value of an option is less sensitive to changes in the risk free interest rate than to changes in other parameters. For this reason, rho is the least used of the first-order Greeks.Practical use
Rho is typically expressed as the amount of money, per share of the underlying, that the value of the option will gain or lose as the risk free interest rate rises or falls by 1.0% per annum (100 basis points).Charm
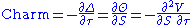 |
Charm or delta decay, measures the instantaneous rate of change of delta over the passage of time. Charm has also been called DdeltaDtime. Charm can be an important Greek to measure/monitor when delta-hedging a position over a weekend. Charm is a second-order derivative of the option value, once to price and once to the passage of time. It is also then the derivative of theta with respect to the underlying's price.
Practical use
The mathematical result of the formula for charm (see below) is expressed in delta/year. It is often useful to divide this by the number of days per year to arrive at the delta decay per day. This use is fairly accurate when the number of days remaining until option expiration is large. When an option nears expiration, charm itself may change quickly, rendering full day estimates of delta decay inaccurate.Color
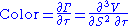 |
Color, gamma decay or DgammaDtime measures the rate of change of gamma over the passage of time. Color is a third-order derivative of the option value, twice to underlying asset price and once to time. Color can be an important sensitivity to monitor when maintaining a gamma-hedged portfolio as it can help the trader to anticipate the effectiveness of the hedge as time passes.
Practical use
The mathematical result of the formula for color (see below) is expressed in gamma/year. It is often useful to divide this by the number of days per year to arrive at the change in gamma per day. This use is fairly accurate when the number of days remaining until option expiration is large. When an option nears expiration, color itself may change quickly, rendering full day estimates of gamma change inaccurate.DvegaDtime
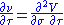 |
DvegaDtime, measures the rate of change in the vega with respect to the passage of time. DvegaDtime is the second derivative of the value function; once to volatility and once to time.
Practical use
It is common practice to divide the mathematical result of DvegaDtime by 100 times the number of days per year to reduce the value to the percentage change in vega per one day.Gamma 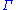
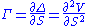 |
Gamma,
 , measures the rate of change in the delta with respect to changes in the underlying price. Gamma is the second derivative
, measures the rate of change in the delta with respect to changes in the underlying price. Gamma is the second derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the value function with respect to the underlying price. All long options have positive gamma and all short options have negative gamma. Gamma is greatest approximately at-the-money (ATM) and diminishes the further out you go either in-the-money (ITM) or out-of-the-money (OTM). Gamma is important because it corrects for the convexity
Convexity (finance)
In mathematical finance, convexity refers to non-linearities in a financial model. In other words, if the price of an underlying variable changes, the price of an output does not change linearly, but depends on the second derivative of the modeling function...
of value.
When a trader seeks to establish an effective delta-hedge for a portfolio, the trader may also seek to neutralize the portfolio's gamma, as this will ensure that the hedge will be effective over a wider range of underlying price movements. However, in neutralizing the gamma of a portfolio, alpha (the return in excess of the risk-free rate) is reduced.
Lambda
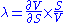 |
Lambda
Lambda
Lambda is the 11th letter of the Greek alphabet. In the system of Greek numerals lambda has a value of 30. Lambda is related to the Phoenician letter Lamed . Letters in other alphabets that stemmed from lambda include the Roman L and the Cyrillic letter El...
,
 , omega
, omegaOmega
Omega is the 24th and last letter of the Greek alphabet. In the Greek numeric system, it has a value of 800. The word literally means "great O" , as opposed to omicron, which means "little O"...
,
 , or elasticity is the percentage
, or elasticity is the percentagePercentage
In mathematics, a percentage is a way of expressing a number as a fraction of 100 . It is often denoted using the percent sign, “%”, or the abbreviation “pct”. For example, 45% is equal to 45/100, or 0.45.Percentages are used to express how large/small one quantity is, relative to another quantity...
change in option value per percentage
Percentage
In mathematics, a percentage is a way of expressing a number as a fraction of 100 . It is often denoted using the percent sign, “%”, or the abbreviation “pct”. For example, 45% is equal to 45/100, or 0.45.Percentages are used to express how large/small one quantity is, relative to another quantity...
change in the underlying price, a measure of leverage
Leverage (finance)
In finance, leverage is a general term for any technique to multiply gains and losses. Common ways to attain leverage are borrowing money, buying fixed assets and using derivatives. Important examples are:* A public corporation may leverage its equity by borrowing money...
, sometimes called gearing.
Speed
 |
Speed measures the rate of change in Gamma with respect to changes in the underlying price. This is also sometimes referred to as the gamma of the gamma or DgammaDspot. Speed is the third derivative of the value function with respect to the underlying spot price. Speed can be important to monitor when delta-hedging or gamma-hedging a portfolio.
Ultima
 |
Ultima measures the sensitivity of the option vomma with respect to change in volatility. Ultima has also been referred to as DvommaDvol. Ultima is a third-order derivative of the option value to volatility.
\frac{\partial^2 V}{\partial S \partial \sigma}
|}
Vanna, also referred to as DvegaDspot and DdeltaDvol, is a second order derivative of the option value, once to the underlying spot price and once to volatility. It is mathematically equivalent to DdeltaDvol, the sensitivity of the option delta with respect to change in volatility; or alternatively, the partial of vega with respect to the underlying instrument's price. Vanna can be a useful sensitivity to monitor when maintaining a delta- or vega-hedged portfolio as vanna will help the trader to anticipate changes to the effectiveness of a delta-hedge as volatility changes or the effectiveness of a vega-hedge against change in the underlying spot price.
Vomma
 |
Vomma, Volga, Vega Convexity, Vega gamma or dTau/dVol measures second order sensitivity to volatility
Volatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
. Vomma is the second derivative of the option value with respect to the volatility, or, stated another way, vomma measures the rate of change to vega as volatility changes. With positive vomma, a position will become long vega as implied volatility increases and short vega as it decreases, which can be scalped in a way analogous to long gamma. And an initially vega-neutral, long-vomma position can be constructed from ratios of options at different strikes. Vomma is positive for options away from the money, and initially increases with distance from the money (but drops off as vega drops off). (Specifically, vomma is positive where the usual d1 and d2 terms are of the same sign, which is true when d2 < 0 or d1 > 0.)
Zomma
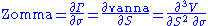 |
Zomma measures the rate of change of gamma with respect to changes in volatility. Zomma has also been referred to as DgammaDvol. Zomma is the third derivative of the option value, twice to underlying asset price and once to volatility. Zomma can be a useful sensitivity to monitor when maintaining a gamma-hedged portfolio as zomma will help the trader to anticipate changes to the effectiveness of the hedge as volatility changes.
Black–Scholes
The Greeks under the Black-Scholes model are calculated as follows, where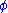 (phi) is the standard normal probability density function
(phi) is the standard normal probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
and
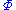 is the standard normal cumulative distribution function
is the standard normal cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
. Note that the gamma and vega formulas are the same for calls
Call option
A call option, often simply labeled a "call", is a financial contract between two parties, the buyer and the seller of this type of option. The buyer of the call option has the right, but not the obligation to buy an agreed quantity of a particular commodity or financial instrument from the seller...
and puts
Put option
A put or put option is a contract between two parties to exchange an asset, the underlying, at a specified price, the strike, by a predetermined date, the expiry or maturity...
.
For a given:
Stock Price
 ,
,Strike Price
 ,
,Risk-Free Rate
 ,
,Annual Dividend Yield
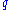 ,
,Time to Maturity,
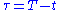 , and
, andVolatility
 ...
...| Calls | Puts | |
|---|---|---|
| value | 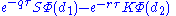 |
 |
| delta |  |
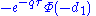 |
| vega |  |
|
| theta | 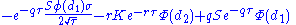 |
 |
| rho | 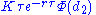 |
 |
| gamma |  |
|
| vanna | 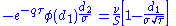 |
|
| charm | 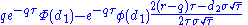 |
 |
| speed | 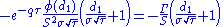 |
|
| zomma | 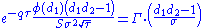 |
|
| color | 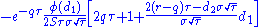 |
|
| DvegaDtime | 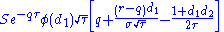 |
|
| vomma | 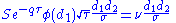 |
|
| Ultima | 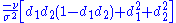 |
|
| dual delta | 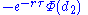 |
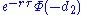 |
| dual gamma | 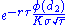 |
|
where
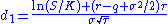

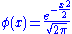

Bond duration
In trading of fixed interest securities (bonds), various measures of bond durationBond duration
In finance, the duration of a financial asset that consists of fixed cash flows, for example a bond, is the weighted average of the times until those fixed cash flows are received....
are used analogously to the delta of an option. The closest analogue to the delta is DV01, which is the reduction in price (in currency units) for an increase of one basis point
Basis point
A basis point is a unit equal to 1/100 of a percentage point or one part per ten thousand...
(i.e. 0.01% per annum) in the yield (the yield is the underlying variable).
Analogous to the lambda is the modified duration, which is the percentage change in the market price of the bond(s) for a unit change in the yield (i.e. it is equivalent to DV01 divided by the market price). Unlike the lambda, which is an elasticity
Elasticity (economics)
In economics, elasticity is the measurement of how changing one economic variable affects others. For example:* "If I lower the price of my product, how much more will I sell?"* "If I raise the price, how much less will I sell?"...
(a percentage change in output for a percentage change in input), the modified duration is instead a semi-elasticity—a percentage change in output for a unit change in input.
Fugit
The fugitFugit
In mathematical finance, the fugit is the optimal date to exercise an American or Bermudan option. It is useful to compute it for hedging purpose.- Origin:...
is the optimal date to exercise an American or Bermudan option. It is useful to compute it for hedging purposes—for example, one can represent flows of an American swaption like the flows of a swap starting at the fugit multiplied by delta, then use these to compute sensitivities.
See also
- Alpha (finance)
- Beta coefficientBeta coefficientIn finance, the Beta of a stock or portfolio is a number describing the relation of its returns with those of the financial market as a whole.An asset has a Beta of zero if its returns change independently of changes in the market's returns...
- Delta neutralDelta neutralIn finance, delta neutral describes a portfolio of related financial securities, in which the portfolio value remains unchanged due to small changes in the value of the underlying security...
- Greek letters used in mathematicsGreek letters used in mathematicsGreek letters are used in mathematics, science, engineering, and other areas where mathematical notation is used as symbols for constants, special functions, and also conventionally for variables representing certain quantities. In these contexts, the capital letters and the small letters represent...
External links
Discussion- Why We Have Never Used the Black-Scholes-Merton Option Pricing Formula, Nassim TalebNassim TalebNassim Nicholas Taleb is a Lebanese American essayist whose work focuses on problems of randomness and probability. His 2007 book The Black Swan was described in a review by Sunday Times as one of the twelve most influential books since World War II....
and Espen Gaarder Haug
Theory
- Delta: quantnotes.com,
- Delta, Gamma, GammaP, Gamma symmetry, Vanna, Speed, Charm, Saddle Gamma: Vanilla Options - Espen Haug,
- Volga, Vanna, Speed, Charm, Color: Vanilla Options - Uwe Wystup, Vanilla Options - Uwe Wystup
Online tools
- Surface Plots of Black-Scholes Greeks, Chris Murray
- Online real-time option prices and Greeks calculator when the underlying is normally distributed, Razvan Pascalau, Univ. of Alabama
- Excel-based tool to calculate the Greeks - A free excel sheet provided by Pristine


 )
)  )
)  Delta
Delta  Vega
Vega  Theta
Theta 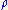 Rho
Rho )
)  Gamma
Gamma  )
)  )
)